Principles of Teaching and Learning
John Denker
* Contents
1 Overview
-
Emphasize motivation. This includes
encouraging curiosity and the love of learning for its own sake. It
also includes explaining the practical value of what is being
learned.
-
Emphasize learning as opposed to mere teaching.
It doesn’t directly matter what you teach; it matters what the
students learn.
-
Emphasize personal responsibility.
Learning is the students’ responsibility; you cannot do it for them.
Your job is to inspire them and help them to fulfill their
responsibilities.
Responsibility can be taught, bit by bit, over the long haul. The
topic of responsibility should be addressed directly. It should be
discussed early and often. There should be clear rewards for
responsible behavior.
I tell students that more than 90% of what they need to know, they
need to learn on their own. All I can do is help get them started in
the right direction.
-
It helps to know where the students are coming from.
A useful proverb is:
Learning proceeds
from the known
to the unknown.
|
|
|
|
To say the same thing the other way, you cannot explain idea X in
terms of idea A unless the students already understand idea
A.
-
Accentuate the positive, and emphasize constructive
suggestions. In particular, start by teaching the correct ideas, as
opposed to starting by confronting misconceptions.
For details on this, see section 3.
-
Students can’t learn everything at once, but
they have to start somewhere.
That is: If the long-term goal is for the students to have
a comprehensive, detailed, sophisticated, rigorous understanding
of the subject, they can’t learn that on the first day.
Typically the students start by learning some examples, analogies, and
approximations. This should include explicit disclaimers emphasizing
that the examples are not entirely representative and the
approximations are not exactly accurate. Next the students should
learn some math and some theoretical principles, which they can apply
to the examples. Also they should always make every effort to see the
connections between the new information and everything else they know.
Then they should spiral back and learn a wider range of examples,
better approximations, more math, more theory, and more connections.
And so forth, iteratively.
-
Explicitly teach students how to learn, and how to
remember what they have learned.
There are a number of standard techniques to help with memory, some of
which date back 2500 years.
Memory should not be thought of as a substitute for critical thinking,
or vice versa. Indeed, memory itself is a thought process.
Being able to recall relevant information is a necessary ingredient
for critical thinking.
-
If you want to improve your memory, it is far from
sufficient to think “harder” about something at the time it must be
recalled. Instead, one must make the effort to form useful memories
at the time the memory is laid down, days or months or years before it
is needed. It takes time and effort to lay down such memories. As
mentioned in item 6, thinking about the connections
(aka associations) between ideas is important. More than 100 years
ago, in reference 1, William James wrote this about each
remembered idea:
Each of the associates is a hook to which it hangs,
a means to fish it up when sunk below the surface. Together they
form a network of attachments by which it is woven into the entire
tissue of our thought. The ‘secret of a good memory’ is thus the
secret of forming diverse and multiple associations with every
fact we care to retain.
Thinking about the connections between a newly-learned idea and older
ideas is first of all a check on the correctness and consistency of
the ideas, and secondly serves to reinforce the memory of both the new
and old ideas.
To say the same thing another way: A rote memory can be recalled in
one way, so technically it counts as a memory, but it is not a very
useful memory. In contrast, a well-constructed memory can be recalled
in 100 different ways, which makes it 100 times more useful.
-
There is a fine line between an approximation and
a misconception.
In teaching, as in every other facet of life, approximations are
necessary. On the other hand, any approximation can be abused.
This topic needs to be taught – directly, emphatically, early, and
often. Students need to learn to think clearly about approximations
in general, not just this-or-that approximation du jour.
Things they need to know include:
- Not all approximations are created equal. There are good
approximations, mediocre approximations, and bad approximations. It
takes skill and judgment to know the difference between a good
approximation and a bad approximation in any given situation.
- Whenever possible, it is desirable to have a controlled
approximation. For example, it is of some limited value to say π
is approximately 3.1, but it is incomparably more valuable to say that
π is greater than 3.1 and less than 3.2. The latter is a
controlled approximation, which means you know how accurate is. You
know the limits of validity of the approximation.
-
Preservice and novice teachers beware: the space
of misconceptions is larger than you can possibly imagine. Just
because you were never confused about this-or-that doesn’t mean your
students won’t be confused about it. That’s one of the many reasons
why you give tests: to find out what you didn’t cover sufficiently
well.
-
Don’t become part of the problem. The usual advice is,
don’t teach misconceptions, and don’t teach nonsense.
That advice is harder to follow than it might seem, because we are
constantly besieged by misconceptions and nonsense. This includes the
misconceptions we grew up with. The misconceptions and nonsense are
particularly pernicious when they appear in textbooks and in
state-mandated “standards” and tests.
Almost any topic can be taught in N different ways, most of which
will cause trouble later, and only a few of which form a good
foundation for further work.
Just because it was badly taught to you doesn’t dictate that it
must be badly taught by you.
-
If a student seems confused or hesitant, don’t be shy about
asking the student what the problem is. Sometimes they don’t know
what the problem is ... but sometimes they do.
-
Learn from other teachers. Whenever
possible, drop in on other teachers, to see how they handle things.
-
Learn from your students. I have a long
list of nifty ideas I learned from my students.
-
Do not tolerate cheating.
It is sometimes claimed that in the long run, the cheaters harm only
themselves, but it is not true. Sometimes jobs, scholarships, and
even the privilege of staying in school are awarded partly on the
basis of grades, and unfair grades can cause serious harm to innocent
students and third parties.
In particular, you must not tolerate any situation where students who
are not predisposed to cheat feel obliged to cheat just to keep up.
I don’t want to live in a culture where cheating is considered normal.
School should not train people to think that cheating is normal.
-
Do not tolerate plagiarism, since it is a form of
cheating.
-
More generally, do not tolerate anything that gives an
unfair advantage to some students over others.
For example, you should assume that some students will have access to
the questions and answers to tests given in previous years, filed away
in fraternities, private homes, et cetera. I mention this because
even if such files are not against the rules, they are unfair, because
not all students have equal access to the files. Making a rule
against such files is not helpful, because it is more-or-less
unenforceable.
Therefore: do not re-use previous years’ questions, unless you have
made sure that all students have equal access to the questions and
answers.
Constructive suggestion: If you want to re-use any questions from
previous years, you can level the playing field by making previous
years’ questions and answers available, on the web or otherwise.
By way of example, consider the tests given by the Federal
Aviation Administration. For each test, there is a pool of
approximately 1000 possible questions, of which a few dozen appear on
any given instance of the test. The questions are a matter of public
record, but the large size of the pool discourages rote memorization,
since most people find it easier to to learn the underlying principles
than to memorize specific answers to specific questions.
If you want to re-use a question from a previous year, another way to
encourage understanding (as opposed to mere rote regurgitation) is
to rejigger the question so that even though the idea is the same,
the answer is not literally the same.
2 Some Remarks on Style of Teaching
2.1 Don’t Teach as You Were Taught
A word of advice:
|
Don’t teach as you were taught.
|
|
|
|
I was explicitly told that by a mentor, back when I was getting into
the teaching business.
- For one thing, obviously, if everybody were to
teach as they were taught, there would never be any progress.
- Meanwhile, there is a less-obvious and far more interesting
reason: Don’t teach as you were taught. Students will make mistakes
you never dreamed of making yourself, and you have to be prepared for
that. Don’t even teach the way you wish you were taught. The
students are coming from a different place, and they will need things
you didn’t ever need yourself. Give them what they need, not what you
would have needed.
This applies to pretty much everything, not just lectures.
2.2 Be Prepared, but Don’t Be Too Slick
Ironically, sometimes students learn a tremendous amount from a
situation where the teacher makes a mistake, catches the mistake, and
deals with the consequences. That’s important ... and very tricky to
do properly.
As usual, all the extremes are wrong. Yes, it is possible for the
teacher to be too slick, too over-prepared ... but it is of course
possible, easier, and far more common to be under-prepared, which not
good either.
Again, this applies to pretty much everything, not just lectures.
It is also super-dependent on where the audience is coming from. The
level of slickness that is appropriate for an invited talk at the
annual American Physical Society meeting is wildly different from
what’s appropriate in September in the introductory physics course.
For starters, consider the ultra-basic advice:
-
Show the work.
- Check the work.
- Show the checks.
|
The introductory students “should” have been exposed to
this advice every year for the last 10 years ... but they probably
haven’t. What’s worse, they probably haven’t been exposed to anything
complicated enough to make scrupulous checking worth the trouble.
Therefore it is important for them to see you carry out the checks.
|
|
In contrast, the APS audience already knows the importance of
checking, and assumes you checked the results 17 different ways at
home. Therefore they don’t need to see the details.
|
As a related point, the introductory course isn’t just about physics
factoids; it’s also about problem-solving techniques. So it’s
important for students to see how it works when you make a mistake,
catch the mistake, fix the mistake, and proceed from there.
True story: I learned some of this by watching Richard Feynman. One
day he was going over the midterm in an undergraduate course. In the
middle of solving one of the problems, he mentioned that a lot of
students had made a certain mistake. He spent some time explaining
how to recognize that mistake, and (!) a whole family of similar
mistakes, so as to make it easy to stay on the strait-and- narrow path
in the future.
Think about it: Feynman never made that mistake in his life, not
recently, not when he was an undergraduate, not ever. He was way
too smart for that. So how did he know that the students were
vulnerable? It wasn’t from grading the papers; he had TAs to do the
grading. Here’s how it really worked: He talked to the graders,
looked over a sample of the graded papers, and then talked to some
smallish percentage of the students. (This is what he didn’t
do enough of when presenting his famous lectures in 1961/62 and
62/63. Evidently he learned from the experience.)
So, ironically, students got to see him deal with a mistake, not
because he was under-prepared, but because he was more prepared than
most of them could imagine. He was of course prepared to discuss
the right answer, but he was also prepared to say useful things
about the wrong answers. He put serious time and effort into it,
far more than the minimum required.
On the other hand, it would have been even better to teach students
how to stay on the strait-and-narrow path before the midterm.
Making mistakes is part of the game, but it is better done on
homework rather than on the midterm. So there is room for
improvement.
Again, I am not arguing in favor of being under-prepared. For
most teachers, being under-prepared is not an option; they know the
material backwards and forwards and they will never be able to unlearn
it. The point is, being under-prepared forces you to go slowly
... but the skilled teacher can go slowly without being
under-prepared. Being under-prepared forces you to show the
intermediate steps, show the checks, and recover from mistakes ... but
the skilled teacher does all that without being under-prepared.
It’s a bit ironic, but this is one of the ways in which a video is
better than a live lecture: the student can pause and/or backspace the
video. So being “too slick” is slightly less of a problem on video
than it is in person. Different students need different pauses ...
different amounts in different places. Books can also be paused. Web
documents with lots of hyperlinks are even better.
Although finding and fixing mistakes is part of the game, mistakes
should not be the first thing students see. They should see the
right approach at least 10 times before they start encountering
mutations. Otherwise they pick up misconceptions that are super-hard
to unlearn, as discussed in section 3. So this is yet another
reason why being under-prepared is not advantageous; you want to
control how and when the mistakes are introduced. You can even
telegraph the mistake in advance: “Let’s redo the calculation and see
what would have happened if we didn’t keep enough guard digits....”
The idea of learning from mistakes applies to students also, not just
to teachers. Often they learn more from lessons where they screwed up
and then had to deal with the consequences.
At the next level, at some point not too near the beginning of
the course, students need to learn how to handle ill-posed questions,
where there is no answer that fits all the facts, as discussed in
reference 2. Such questions abound in the real world. The
under-prepared teacher will generate plenty of these by accident,
which is not good. The skillful teacher will control the
introduction of such questions, after explaining how to deal with
them.
2.3 Fewer Arbitrary Rules, More Reasons
More than once upon a time, there was a young student who kept
getting bad grades on the assignments, because he didn’t show
the work.
Student: The answers are correct, aren’t they?
Teacher: Yes, but you have to show the intermediate steps.
Student: There aren’t any intermediate steps. I just
figured it out.
Teacher: But you have to show the intermediate steps.
Student: Why?
Teacher: It’s the rules. Don’t blame me; I don’t make
the rules.
Teachers complain bitterly when students blindly follow some procedure
without understanding what they’re doing. However, they shouldn’t be
surprised. All too often, the entirely foreseeable effect of the
lesson is to encourage conformity and obedience, while discouraging
reasoning.
Every member of the school board emphasizes that they want to
encourage critical reasoning. In our example, the student wasn’t
asking for a rule; he was asking for a reason.
The following should be treated as advice, not as arbitrary rules:
- Show the work. This makes it easier to check the work.
- Check the work. Although this may slightly increase the
workload in the short run, it greatly reduces the workload in the
long run, especially when dealing with complex problems.
- Show the checks. This is particularly helpful in a
teamwork situation.
In contrast, when the student is given a non-complex non-teamwork
situation, it doesn’t make sense to convert this advice into a set of
arbitrary and unhelpful rules.
Education is supposed to help the student. The teacher’s job is to
make sure it really is helpful, and then to make sure the student
recognizes it as helpful.
In this particular example, good ways to proceed
include:
- Assign the student a more challenging multi-step problem, so
that checking the work at each step along the way has value to
student – direct, immediate, and perceptible value.
- Create a teamwork situation, where explaining and documenting
the steps has value – direct, immediate, and perceptible value.
3 Dealing with Misconceptions
3.1 Emphasize Correct Conceptions
Whenever the topic of misconceptions comes up,
there is an important contrast that needs to be made:
|
Explaining the correct conceptions should always come first.
|
|
Confronting misconceptions can come later, if at all.
|
|
“The light shines in the darkness, and the darkness cannot
overcome it.”
|
|
“You cannot beat something with nothing.”
|
|
By way of analogy: If you have a healthy lawn, you won’t have
much trouble with weeds. They can’t compete.
|
|
If the lawn is weak and
sparse, due to insufficient water and fertilizer or otherwise, weeds
will invade.
|
|
|
|
In an unhealthy lawn, if you just cut off the top of a
weed, it will grow back. Even if you manage to kill the weed, it is
likely to be replaced by some other weed. See
figure 1.
|
|
Correct ideas need to be linked to each other, and supported
by evidence.
|
|
Misconceptions do not exist in a vacuum; they are
supported by their own evidence. If you simply contradict a
misconception, it will grow back, sooner or later, probably sooner.
Furthermore, often an imperfect notion
contains a germ of truth, so if you flatly contradict the
whole notion you’re not even correct.
|
|
On this web site, there are hundreds of documents that try to
explain correct ideas.
|
|
On this site, there is only one part of one
document – section 4 – that has focuses on
misconceptions, and it should not be the starting point.
|
If you are tempted to search the PER literature for a list of
misconceptions, my advice is: Don’t go there! Reasons for not
going there include:
- The literature will tell you that students have more
misconceptions than you could possibly imagine ... but if you have
any teaching experience at all, you already know that.
- There are so many misconceptions that it would be
impossible to list them all, let alone analyze them.
- It is OK for teachers to talk amongst themselves about
this-or-that misconception, but talking about it in front of students
is at least as likely to reinforce the misconception as to dispel it.
- This brings us back to the main point: To a first approximation,
with isolated exceptions, the best policy is to teach the correct
concepts and move on.
Figure 1 is one way of visualizing the situation.
If students move randomly away from any
given bad idea (shown in red), they are more likely to settle onto a
new bad idea than onto a good idea (shown in blue). You need
to attract them to the good idea, not merely push them away
from this-or-that bad idea.
 Figure 1
Figure 1: Lead Toward Good, Not Merely From Bad
We now turn to figure 2, which is another way of
visualizing the situation. Imagine a very narrow path through a vast
swamp. The path is safe, and everywhere else is unsafe. If you pick
a random point in the swamp, there is a 99.99999% chance you don’t
want to visit that place, or even talk about that place.
One valid path from A to B is shown in black. (There may be more
than one valid path, but even taken together, the valid paths are a
subset of measure zero in the overall space.)
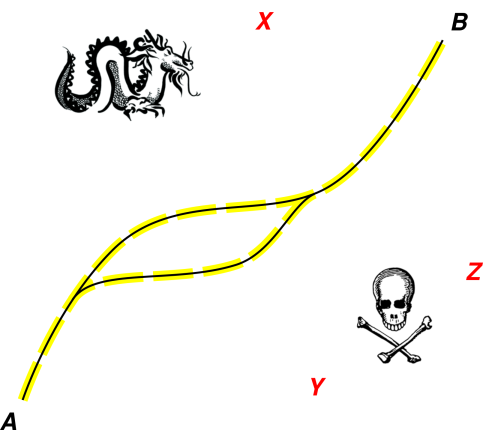 Figure 2
Figure 2: Stay On (or Near) the Valid Path
On rare occasions, as you lead students along the path, you might
want to point out something nasty that is just next to the path, so
they can recognize it and avoid it (as indicated by the yellow places
in the diagram). Still, even so, it is usually easier to recognize
the path than to recognize the nasties. This is the Anna Karenina
principle: All happy students are alike, but every unhappy student is
unhappy in his own way. In more detail: Every student who
understands the material understands it in more-or-less the same way,
but every student who is confused is confused in his own way.
In a one-on-one teaching situation, you can sometimes afford to deal
with misconceptions as they come up. However, this is tricky and
hard to plan, because students often come up with weird
misconceptions that you never dreamed of. Meanwhile, in a classroom
situation, things are even worse, because each student is going to
have a different set of misconceptions.
- The misconceptions most worth worrying about are the ones that
are exceptionally prevalent and exceptionally pernicious. The
classic example concerns the washed-out bridge. As discussed in
section 3.4, it is well worth confronting misconceptions
of this kind.
Section 4 contains a list of misconceptions that
seem particularly prevalent. Please keep in mind that compiling
and/or studying such lists is usually not a good use of resources.
- I’m not so much worried about the misconceptions that the
students bring to class as the misconceptions that the teacher and
the textbook author bring to class. These are called
didactogenic misconceptions, as discussed in section 3.2. They can cause tremendous difficulties for the
students in later courses, and in later life.
Remember that it is proverbially difficult to unlearn something.
Some textbooks contain large numbers of misconceptions. For an
example – not even the worst example – see reference 3.
- Most of the people who collect lists of misconceptions don’t
understand the subject well enough to know what’s a misconception and
what’s not.
On top of that, even though statistics will tell you what’s common
and what’s not, that is nowhere near sufficient; it takes serious
judgment to decide what’s important and what’s not.
- Reading the PER literature is definitely a source of
misconceptions. I don’t mean you will get a tidy list of avoidable
misconceptions labeled as such; I mean that after reading the
literature, if you believe what it says, you will suffer from more
misconceptions than you started with.
For example, the book by Arons, Teaching Introductory Physics
is — unintentionally — an extensive compendium of bad
pedagogy and wrong physics. For a detailed review,
including a list of some of the misconceptions propagated
and/or introduced by this book, see reference 4.
3.2 Didactogenic Misconceptions
A great many misconceptions are created by the way the subject is
taught. We call these didactogenic misconceptions. For
example, ask yourself which will reach the ground first: a ball thrown
downwards or an identical ball thrown horizontally from the same
height? According to reference 5, only students who had
taken physics got this wrong.
Many didactogenic misconceptions are preventable. So, one
might naïvely think the solution would be to put a big sign at the
back of the classroom where the teacher can see it: DON’T TEACH
WRONG STUFF.
That would be consistent with the recommendation of wise guys
of every era, from Hippocrates to Henny Youngman.
However, for reasons discussed above, that’s not the whole story.
We need to take a more nuanced view. I say there are roughly three
categories of misconceptions:
-
A great many are easily preventable, such as the
aforementioned misconception about the ball thrown downwards.
- Some are not so easily preventable. This includes problems
caused by ambiguities that are built into the language we use.
- Some are not preventable, and are just part of the cost of
doing business. For example, as discussed in reference 6,
it is impossible to teach everything at once, so each idea must be
introduced before it is fully explained. This leaves an opening in
which misconceptions can grow. We try to minimize this, but we
cannot eliminate it.
(Tangential remark: This trichotomy appies
to misconceptions in general, but for now let’s keep focusing on
didactogenic misconceptions in particular.)
To a highly nontrivial degree, teaching involves managing
whatever misconceptions arise ... without entirely preventing them.
Sometimes this involves making a mess and then spiraling back to clean
up the mess before too much damage has been done. Cleaning up messes
is expensive, but a strict no-mess policy would be impossible.
Clarification: When I say teaching involves managing misconceptions,
that means (with rare exceptions) encouraging correct ideas rather
than directly confronting incorrect ideas. As discussed in
section 3.1, the maxim should be: “The light shines in
the darkness, and the darkness cannot overcome it.” Similarly,
another maxim is: “A healthy lawn crowds out weeds.” There is a lot
of evidence that talking about a misconception is more likely to
reinforce it than to dispel it. In addition, there is the Anna
Karenina principle: given 30 students, they will have 75 different
misconceptions, and it is simply not possible to directly address them
all. To clean up the mess, you do not need to understand every
detail of the mess.
Also: The whole idea of “didactogenic misconceptions” is a
bit of a chimera:
- It includes situations where the teacher or the textbook
says stuff that is just plain wrong and easily fixable. There
is a lot of this, and we need to fix it, but it is not the
whole story.
- It include situations where everything the teacher says is true
in some hyper-technical sense, but you just know it will lead to
misconceptions. Obvious examples include when the teacher says “In
this situation, the entropy is S = log W.” You just know the
students will forget the proviso and overgeneralize the formula.
They have an example and no counterexamples, so they have no way of
knowing the limits of validity. Rigorously restricting it to this
one particular example would make the result useless, so they know
that can’t be what the teacher means. Overgeneralizing is
sophomoric, but that’s what sophomores do.
Constructive suggestion: If you’re writing a textbook, please footnote
this kind of stuff. Say at least something about the range of
validity. For example, if you write S = log W, please add a
footnote saying something like “this is valid in a microcanonical
situation only. See page 456 for a more robust expression.”
This idea applies to the definition of “entropy”, the definition of
“atom”, the definition of “energy”, and a thousand other things
that cannot be understood in terms of a pithy, dictionary-style
definition. The only hope is to introduce the idea early on, and then
spiral back again and again, refining and enriching the idea.
Rationale: A textbook is not an ideal reference book (nor vice versa).
The organization is completely different. The spiral approach is
appropriate for a textbook but not for a reference book. However,
people use their textbooks as references nevertheless. I get really
tired of arguing with people who say the entropy «MUST» be equal to
log W because it says so right there on page 123 of the textbook.
Ditto for the definition of “atom” and “energy” and a thousand
other things. If we could make students aware of the more robust
discussion on page 456, everybody would be better off. They don’t
need to hear the whole story on the first trip around the spiral, but
they need to know there is more to the story.
Another constructive suggestion, from the keen-grasp-of-the-obvious
department: Don’t teach stuff that is completely wrong. Don’t teach
lousy approximations when better approximations are easily available.
Don’t teach stuff that is 100 years out of date, when the modern stuff
is simpler and better. Don’t create big messes for no reason.
Cleaning up misconceptions is very expensive. Just because some
misconceptions is inevitable does not give you a license to create
misconceptions with reckless abandon.
There is waaaay too much wrong stuff in textbooks nowadays. When I
look through a so-called «modern, research based» textbook from a
«Big Name» publisher, I see hundreds of easy-to-fix conceptual
errors, without even looking very hard. I’m talking about serious
conceptual errors, not counting typos, and not counting multiple
occurrences of the same error.
3.3 Reasons for Not Confronting Misconceptions
At the beginning of the course – and more generally when speaking
with people who do not already trust you – it is best to start by
talking about things that are true, useful, and non-controversial.
Just because something is a misconception does not mean you have
to confront it at the first opportunity.
There is abundant research that shows that mentioning a misconception
is as likely to reinforce it as to dispel it; see reference 7.
Indeed, one often observes a backfire effect, as discussed in
reference 8: The more you talk about something, even in
unfavorable terms, the more likely people are to take it seriously.
What’s worse is that if you are speaking to a stranger and confront
one of their deeply-held beliefs, not only will they not take your
word on it, they will thereafter not take your word on anything else.
Remember, most people are not scientists. They do not evaluate ideas
by weighing the evidence. They believe things that they hear from
people they trust, by people who are on The Team, and if you start out
by being confrontational they will classify you as not part of their
team.
Sometimes bystanders suggest that not confronting misconceptions
implies a lack of courage. If you know something is wrong, why not
speak up about it? To that I reply: “I have plenty of courage, and I
speak up for my convictions in the most effective way I can. I
increase my effectiveness by distinguisning the psychological /
pedagogical issues from the subject-matter issues. Once I have dealt
with the former I will be in a stronger position to deal with the
latter.
3.4 Confronting Misconceptions
Consider the contrast:
|
Sometimes an idea is just completely wrong. Such ideas are
relatively easy to deal with.
|
|
However, in many cases, you are
dealing with a notion that contains a germ of truth. It is
important to recognize this. The most dangerous ideas are the ones
that are usually mostly true, but then betray you at some critical
moment.
|
One classic example of a misconception that is “almost” true
concerns a washed-out bridge. Most people take it for granted that it
is OK to drive across the bridge, and this is usually true,
i.e. usually not a misconception at all. However, if the bridge has
been washed out this becomes a misconception, and could have fatal
consequences. Therefore it is worth putting up some “Bridge Out”
signs and barriers, and possibly even some flashing lights.
As always, it is better to make constructive suggestions, as opposed
to merely pointing out a problem. In this case, it would be silly to
put up a “Bridge Out” sign just at the edge of the washout, because
by the time drivers could see the sign it would be too late to do
anything about it. Instead the proper procedure is to go back to the
previous intersection and block off the approaches to the bridge.
This includes putting up constructive signs suggesting alternate
routes.
- Sometimes the misconception is the result of an ambiguity, as
discussed in section 3.5. That is to say, sometimes a
statement is entirely true if you interpret it one way, but false if
you interpret it another way. In this case it is necessary to deal
with both interpretations. You can’t just close your eyes and
pretend the other interpretation does not exist. The fundamental
mistake – the fundamental misconception – is not recognizing the
ambiguity.
- Sometimes you have to confront a misconception because of the
safety implications. One example is the washed-out bridge.
Similarly, in the research lab you might have high-power invisible
lasers, high voltages, toxic chemicals, and other things that present
non-obvious hazards.
- In contrast, if there are no ambiguities and no safety issues,
then you have the option of confronting the misconception or simply
ignoring it. Often ignoring it is the best option. There is lots of
evidence that mentioning a misconception is at least as likely to
reinforce it as to dispel it.
As an example of a classroom misconception that might be worth
confronting, consider the first law of motion. Practically everybody
starts out with the Aristotelian notion that objects at rest tend to
remain at rest, and objects in motion tend to come to rest. This
directly conflicts with the Newtonian principle that objects in motion
tend to remain in motion.
As is so often the case, we are dealing with a notion that contains a
germ of truth: In situations where friction is overwhelmingly
important and taken for granted, objects do tend to come to
rest. That’s fine. It is OK for students to retain that idea,
provided they learn to distinguish it from situations where
friction is not so important. In physics we start by considering
situations where friction is completely negligible. Later we consider
cases where there is a moderate amount of friction, but even then we
do not take friction for granted, but instead account for it as one of
the forces that change the state of motion.
Again, we want to do this in a constructive way. That requires:
- First, explaining the new concept and supporting it with
reasonable amounts of evidence.
- Secondly, contrasting the new concept with the old concept.
- Only then does it make sense to explain what part of the
old concept is considered a misconception.
It must be emphasized that it is pointless (or worse) to contradict
the old idea before the new idea has been presented. It is not
helpful to push students away from a bad idea unless/until they have a
good idea to latch onto.
The same principle applies to everyone you deal with, not just
students. It applies at every age, from infancy on up. For example,
if a young child is banging a Wedgwood teacup against the tile floor,
it is better to give the kid something else to play with, rather than
simply taking the teacup away. A small plastic bottle with a few
dried beans inside makes a much better toy, from everyone’s point of
view.
3.5 Ambiguities and Bisconceptions
It is quite common to find several different, incompatible ideas
masquerading behind the same name. This is a perennial source of
difficulty.
Unless we specify the context, none of these ideas can properly be
called misconceptions (i.e. wrong ideas). I prefer to call them
bisconceptions (i.e. two ideas). Here are some examples:
- Very commonly, the homespun meaning of a word conflicts with the
technical meaning. Consider the contrast:
|
In a non-technical context, «force» refers to some sort of
causation, as in “the bandit forced the lady to hand over her
purse.”
|
|
In physics, force has nothing to do with causation; force
does not cause acceleration, nor does acceleration cause force.
|
|
There is absolutely no equal-and-opposite «force».
|
|
For
every force there is an equal-and-opposite force.
|
You cannot force people to believe that
dp/dt is the only meaning of the word “force”.
|
|
|
|
- Even if we restrict attention to technical meanings, there are
still ambiguities. For example:
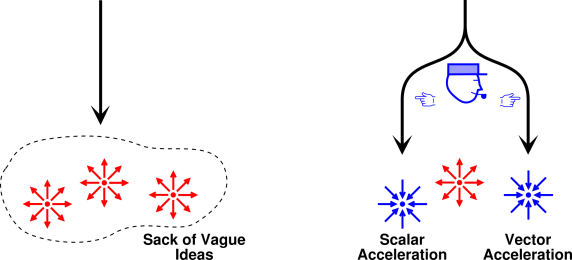
- In physics, there are two notions of acceleration:
|
There is a notion of scalar acceleration, namely the
rate-of-change of the scalar speed. It is the opposite of
deceleration.
|
|
There is also a notion of vector acceleration, namely
the rate-of-change of the vector velocity. There is no corresponding
notion of vector deceleration, only acceleration in the opposite
direction.
|
Introductory physics texts like to pretend that scalar acceleration
is crazy wrong, but in fact physicists use the concept all the time.
People (including physicists) use both concepts all the time, and
there would be nothing wrong with that, except for the fact that they
use the same term for both.
- In physics, there are two different technical meanings of the
word “gravity”.
|
There is the framative gravity g@F (in some frame F).
It is 100% frame-dependent.
|
|
There is also the massogenic
contribution δgM. See reference 9. It is
100% frame-independent.
|
I do not recall ever seeing a textbook make this distinction; the
usual practice is to use the name “gravity” for both, use the
symbol g for both, and then write contradictory equations involving
g.
- Consider the first law of motion: an object in motion tends to
remain in motion. Contrast that with the widely- and deeply-held
opinion that objects in motion tend to come to rest. We can
reconcile these two ideas as follows:a
|
Suppose you are a flagellate bacterium. You live in a
world with a verrrry low Reynolds number. Friction is dominant, and
inertia is an utterly negligible correction.
|
|
Suppose you are an
aircraft. Your Reynolds number is much higher. Inertia is dominant,
and friction is a relatively minor correction term.
|
In the introductory physics class, we choose to start by
considering the low-friction case. Students’ intuition about the
high-friction case is not wrong; it’s just incompatible with our
chosen starting point.
A direct attack on the idea that objects in motion tend to come to
rest will never be successful, because the idea has too much
supporting evidence. The best you can hope for is to place
limits on the validity of the idea, to restrict it to tiny
objects moving slowly through a sticky medium.
- The same attitude works for notions of “heat content” aka
“caloric”. Such ideas are not crazy wrong, and indeed it is
easy to find supporting data. However, such ideas apply only
cramped thermodynamics, i.e. to situations so heavily restricted
that it is impossible to build any kind of heat engine. When
applied out of context, such ideas greatly interfere with any
attempt to understand uncramped thermodynamics.
- In thermodynamics, there are two different definitions of
“adiabatic” in common use. My recommendation is to avoid the word,
and use other terms instead, such as “thermally insulated” or
“gradual and isentropic (as opposed to sudden)”.
- In thermodynamics, there are at least four different technical
definitions of “heat” in common use (not to mention innumerable
nontechnical and metaphorical meanings). I recommend bypassing this
whole mess and instead formulating the subject in terms of energy and
entropy ... without mentioning “heat” at all.
When teaching about bisconceptions, emphasize that context matters.
The meaning of a word in one context is different from the meaning in
another context. Neither meaning is wrong; they’re just different.
The only real misconception, i.e. the only mistake, lies in not
recognizing the distinction, or not being clear about the context.
Often the first step is to clarify the terminology. Sometimes it
suffices to tack on some adjectives, as we saw in the example of
“scalar acceration” versus “vector acceleration”. Sometimes you
have to coin a new term, as we saw in the example of “framative
gravity” versus “massogenic gravity” – and in the example of
“bisconception” itself.
In contrast, I do not recommend choosing one possible meaning and then
waging war against everybody who uses the other meanings.
3.6 Insufficient Specificity
Consider the assertion that “cows are brown”. Is that a
misconception? I don’t know, because I can’t figure out what is being
asserted. Possibilities include:
- Some cows are brown.
- All cows are brown.
Statement (A) is entirely correct, whereas statement (B) is
entirely incorrect.
Many ideas that are a good approximation in one context are a bad
approximation in other contexts. The goal is to formulate a
more-specific version of the idea, containing enough provisos so that
you know which is which.
Here is another example that touches on the notion of specificity:
|
|
|
| In Euclidean geometry, |
| a2 + b2 | | = | | c2 | |
| where abc is a right triangle |
| and c is the hypotenuse
|
| (2)
|
|
|
If you are going to teach people that a2+b2=c2, you have an
obligation to tell them that the result is valid for Euclidean right
triangles only. This is important, because there are lots of
triangles in this world that are not right triangles ... and lots that
are not Euclidean.1
3.7 Recurring Misconceptions
While some misconceptions are only lightly held, others are quite
deeply held, based on the student’s lifetime of experience (in school
and otherwise). As mentioned in section 3.3,
reference 7, and reference 8, when you confront a
deeply-held misconception, students may become wary, defensive, or
even angry. It is likely that the students will pretend to discard
the misconception, but then re-adopt it at the first opportunity.
What’s worse, sometimes direct confrontation can backfire, causing the
student to cling to the misconception even more tightly, and to
discredit the teacher in the process.
If a misconception keeps coming back, there are several possible
explanations, and correspondingly several ways of dealing with the
situation. There are various possibilities, which are not mutually
exclusive:
- There is a grain of truth in most misconceptions, especially
the most pernicious ones.
Therefore you should start by considering the possibility that you
are facing a bisconception. That means there is actually some good
evidence supporting the so-called wrong idea. It’s not entirely
wrong; it’s correct in one context but wrong in another. The only
real mistake is in not recognizing the ambiguity and not being clear
about the context. In such a case, it may be possible to
disambiguate the terminology by adding adjectives, or it may be
easier to switch to completely different terminology for one or more
of the affected concepts. See section 3.5.
It is generally not possible to eradicate the old idea – and not
even worth the attempt – even if the idea is completely unhelpful
in the situations you want to address. Instead you have to build
something new alongside it, as in figure 4
and figure 5.
This requires a delicate tight-rope act. You have to be respectful
of the old idea, even as you are trying to shift attention to the
new ideas. Sometimes it helps to use a two-column format, as in
section 3.5, or other techniques to highlight the
contrasts.
- It may be that the correct conception is not sufficiently
supported. In such a case, it is best to focus on the correct
conception, tying it to additional data and additional reasoning.
Especially in the introductory course, start by delineating the
good things by talking about what they are, not about what the
aren’t. Give them something positive to move toward, as in
figure 1. Sometimes you can delineate something
using the idea of negative space, as in figure 3,
but that’s usually not the first choice.
 Figure 3
Figure 3: Triangle Delineated by Negative Space
- It may be that the misconception is supported by a great deal
of bogus data and fallacious reasoning. In such a case, rather
than directly attacking the symptom, it may be helpful to go
upstream a step or two, and attack the bogus data rather than
whatever misconceived conclusions might derive from it. That is,
figure out what sort of mistaken evidence is supporting the
misconception, and then demonstrate why that evidence is invalid.
Hands-on, live demonstrations play an important role here.
Without mentioning the misconception itself, you can gradually
undermine its supports, one by one.
- It may be a case of insufficient specificity, as discussed in
section 3.6. In such a case, you need to explain why
the notion is correct in some contexts but not in others, and
explain how to tell the difference. A change in terminology might
help (but might not be sufficient by itself).
There is a pedagogical / psychological dimension to this. There is a
mountain of evidence suggesting that established ideas are virtually
never truly unlearned, not on any pedagogically relevant timescale
anyway. Instead the best you can hope for is to hide the bad ideas
behind a wall of better ideas, so that in any given context the right
idea is more likely to be recalled. The wrong (or merely
inapplicable!) ideas are still there; they just won’t be the first
things that come to mind. So, rather than figure 1,
the picture is more like figure 4.
By telling students their ideas are not crazy wrong – just restricted – they are less likely to get defensive. It enhances
the teacher’s credibility. It gives students a framework that
accounts for all the data. This upholds one of the core
principles of critical reasoning: account for all the data.
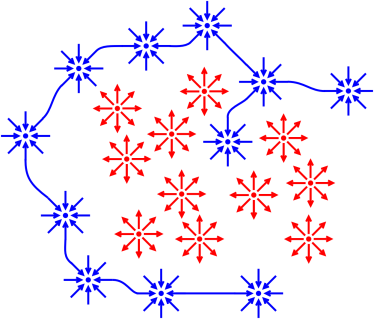
Figure 5 shows an even better version of the idea of
adding a layer. If we choose an idea at random from a sack of
acceleration-related ideas, we will be wrong more than half the time,
as shown on the left side of the diagram. Old ideas never really go
away, but we can add a traffic-cop layer that steers our thoughts in
the right direction, depending on context, as shown on the right.
Ideas that were mostly wrong before are now reliably correct, in
context.
This is consistent with a recurring theme, namely that what matters is
not how many factoids you know, but rather how well you can recall
them when needed. This was mentioned in item 8 in
section 1. There is no clear distinction between thought and
memory, because recall itself is a thought process.
3.8 Detailed Taxonomy of Misconceptions, Preconceptions, etc.
Some people use the word “misconception” in very narrow ways, or
avoid it altogether. One teacher sent me a list of thirty different
terms intended to describe different types of misconceptions,
preconceptions, and related ideas.
With rare exceptions, I am not interested in such fine distinctions,
because the methods of dealing with them are the same for all. I use
words like “idea” and “notion” in a broad sense, including ideas
that are completely correct, completely incorrect, and everything in
between. Almost all ideas are imperfect in some way. I use the term
“misconception” to apply to whatever part of the idea is incorrect.
I make an exception for the term bisconception, which I use to make
the point that many things are commonly called misconceptions aren’t
entirely wrong; they’re just out of context.
4 A Few Prevalent Misconceptions
The following list is restricted to misconceptions that afflict
professionals in the field. (There is of course a far wider class of
misconceptions that afflict naïve students.)
Another compendium of misconceptions can be found in reference 10. Some related issues of weird terminology are
discussed in reference 11.
Keep in mind that you should always start by emphasizing correct
conceptions, as discussed in section 3.1. To say the
same thing the other way: creating and/or studying lists of
misconceptions is usually not a good idea, and should never be a
starting point.
4.1 Patterns of Bad Reasoning
- Far and away the biggest problem is an overall lack
of critical thinking skills. See reference 12.
This includes, far too often, accepting a “rule” without
differentiating between a “rule of thumb” and a “rule in all
generality”.
This includes learning a “rule” without reconciling it with other
experimental and theoretical things they know.
This includes learning the headline of a rule without learning the
provisos, without learning the limitations on the range of validity
of the rule.
- As a related point: Failure to uphold the simple rule:
-
Show the work.
- Check the work.
- Show the checks.
- Design the work from the outset to be readily checkable.
- Chronic and pervasive inability to tell the
difference between a good approximation and a bad approximation ...
and indeed unawareness that this is even an issue. See
reference 13.
4.2 Miscellaneous Misconceptions
-
Multiple misconceptions about scientific
methods. For example, fixating during the planning stage on a
single hypothesis. Common sense and basic scientific principles
demand considering all the plausible hypotheses. Indeed this
is required for safety if nothing else. See
reference 13.
-
The false notion that scientists change “only one
variable at a time”.
-
Multiple misconceptions about “significant
figures” and/or how to handle uncertainties. See
reference 14. See also item 5.
It is easy to find examples of professors being completely
confident about the wrong answer.
-
That includes pervasive misunderstanding of what
“error” means in the context of “error analysis”. See
reference 14.
-
Innumerable misconceptions about probability.
For example, suppose I toss a fair coin 100 times. On every
“heads”, I take one step to the north. On every “tails”, I
take one step to the south. After the 100th step, how far away am
I, on average, from where I started? (Most kids – and more than a
few teachers – say “zero” ... which is not the right answer.)
-
Widespread misconceptions about the fundamental
principles of quantum mechanics. The fact is that even in fully
quantum mechanical systems, not everything is quantized,
not all waves are quantized, not all states are discrete,
et cetera. See reference 15.
-
Innumerable misconceptions and/or archaic conceptions about
special relativity.
This includes velocity-dependent mass, rulers that can’t be
trusted, clocks that can’t be trusted, et cetera. It is a
misconception to think those are a good idea (even if they are not
provably wrong). Certainly they must be unlearned as a prerequisite
to any modern (post-1908) understanding of special relativity,
spacetime geometry, and 4-vectors ... not to mention general
relativity. See reference 16.
-
Misunderstanding of the famous equation E=mc2. Hint:
this E is the rest energy. If the mass is moving, we need a more
complicated formula. Mass is the invariant norm of the [energy,
momentum] 4-vector. See reference 16.
-
Misunderstanding of general relativity, especially as to what
is curved, and in what direction it is curved. A marble rolling
around inside a bowl does not illustrate general relativity. See
reference 17.
-
Misconceptions about what expands and what
doesn’t – and why it doesn’t – during the expansion of the universe.
See reference 18.
-
The idea that «Kirchoff’s laws are fundamental,
and/or can be directly derived from Maxwell’s equations».
A previous version of the wikipedia article said exactly that
(before I changed it). In fact, for AC circuits, both of Kirchhoff’s
laws are flatly contradicted by the Maxwell equations. Both of
Kirchhoff’s laws are routinely violated in practice. See
reference 19. There are tremendous
misconceptions about this.
-
Assuming that every voltage must be a
potential, and every electric field must be the gradient of some
potential. This assumption is embodied in Kirchhoff’s laws. We
know it can’t be true when there are time-varying magnetic fields
running around.
-
Misconception that thermal energy
(whatever that means) is random kinetic energy to the
exclusion of potential energy. See also item 19. For
details, see reference 20.
-
There are some who try to define energy as “capacity to
do work”. This formulation is fairly common in nonscientific
books. It appeals to those who know nothing about
thermodynamics. See reference 20.
-
Entropy as “disorder”.
-
Entropy as “spreading of energy”.
-
Misconception that
expansion of the universe correlates with thermodynamic
irreversibility i.e. entropy production.
-
Innumerable other misconceptions regarding entropy. See
reference 20.
-
Trying to think of thermodynamics in terms of a
“heat content” or “thermal energy” state function. See
reference 20.
-
Writing d(something) for ungrady one-forms, e.g. dQ =
T dS. (This is somewhat related to item 19.) See
reference 21.
-
Terminology and thought patterns that confuse
“heat” with “enthalpy”, e.g. tables of the “heat of reaction”.
Counterexample: reversible reactions such as electrochemical cells.
Similarly, misconception that heat is conserved (e.g. in the
typical statement of Hess’s law). See reference 20.
-
Holy wars about the various definitions of “heat”. Example:
heat flowing into a system “surely” raises its temperature.2
See reference 20.
-
Confusion about the relationship between energy and
temperature, e.g. Define temperature as the measure of thermal
energy
-
Confusion about the meaning of “intensive”
versus “extensive”. (Possibly confused with intrinsic versus
extrinsic?)
-
Conflict over whether the rate constant
for the reaction x A → y B + z C
should depend on the stoichiometric coefficient x. In particular,
deciding to scale the rate constant by a factor of x without
regard to the order of the reaction. I claim that for an Mth
order reaction, the normalization factor is x(M−1). I claim
you want to define the rate constant per unit of “→” not
per unit of [A].
-
Misconception that electrons must “jump” from
stationary state to stationary state. To say the same thing in NMR
terminology, the misconception is that π/2 or π/10 tipping
pulses are impossible.
-
Misconception that electrons “like” to pair up,
like Siegfried and Roy. In fact, physics says they hate each other.
Spectroscopy (as summarized by Hund’s rule) says that in the ground
state, they pair up only as a last resort.
-
Misconception that breaking a chemical bond
releases energy, the way that breaking an eggshell releases what’s
inside.
-
Misconception that pure water necessarily has pH 7 or
that pH 7 corresponds to neutral conditions, i.e. neither acidic
nor alkaline. In fact, pure water at 100 ∘C has a pH of 6.13 or
thereabouts.
-
Misconception that during changes of
state the temperature remains constant.
-
Multiple inconsistent definitions of “molecule”.
– molecules = “stable particles of matter” is a non-starter,
because water molecules are not stable in aqueous solution.
– molecules are “covalently bonded” is a non-starter, because
many things that ought to be considered molecules are not covalently
bonded.
– molecules obey the “law of definite proportions” is a
non-starter, because many macromolecules do not uphold it.
-
Uncertainty about the definition of “compound”.
-
Related minor point: There seem to be widespread misconceptions
about the definition of “dimer”.
Also note that the IUPAC definition of polymer is very broad,
and does not parallel the definition of dimer.
-
The alleged dichotomy between “ionic
compounds” and “molecular compounds”.
-
The whole notion of “physical change” as
distinct from “chemical change” is disconnected from reality. There
are multiple inconsistent definitions of the terms. All the usual
definitions conflict with the usual examples. See
reference 22 .
-
In most chemistry texts, there is some kind of a
flowchart that uses various crude criteria to classify substances as
elements, compounds or mixtures. This incorrectly implies that it
is impossible for any substance to simultaneously be an element and
a mixture. In particular, it gets you into trouble with an element
that is a mixture of isotopes. The right way to think about this
is in terms of equivalence classes. Things that are “pure” w.r.t
one property may not be “pure” w.r.t to another.
-
Misconception that “Like Dissolves Like”.
-
Le Châtelier’s «principle» is highly problematic.
Le Châtelier in his lifetime gave two inconsistent statements of the
«principle». One is trivially tautological, and the other is
false. See reference 23.
-
Widespread deep-seated misconceptions about osmosis and
osmotic pressure. This includes using glycerin or other
hygroscopic substances as pedagogical examples of osmosis. See
reference 24.
-
Way too much emphasis on the Bohr model of the atom,
i.e. electrons following Keplerian orbits within atoms.
-
There are profound problems with Lewis dot diagrams
in general, and the idea of filled Lewis octets in molecules in
particular. These ideas are are fundamentally inconsistent with all
the spectroscopic data ... and other data. The paramagnetism of
O2 makes for a nice, graphic, in-class demonstration. See
reference 25.
It’s particularly comical when they arrange Lewis dots (falsely
representing electrons) onto little Keplerian circles (falsely
representing orbitals) to make molecules
(falsely suggesting that there are filled “Lewis octets”
in molecules).
-
Talking about “position” of the electron within a
“p orbital”. (These are incompatible variables, incompatible in
the Heisenberg sense.)
-
Uncertainty about “orbitals”. Does the
term refer to wavefunctions describing actual electrons,
or does it refer to basis wavefunctions that are purely
mathematical?
-
The whole idea of oxidation numbers in redox
reactions is grossly abused. When balancing redox reactions, it is
simpler and better to just use conservation of charge, directly.
See reference 26.
-
Arons asserts there are two kinds of electrical
charge. He says the two-fluid model is right, and the
one-component model is wrong. See reference 27
for a refutation.
-
Arons also suggests teaching students the
difference between “passive forces” and “active forces”.
-
Questions about where the lanthanoids and
actinoids belong in the periodic table. There should not be any
questions. These are basically elementary fencepost errors.
See reference 28.
Also, a related bundle of misconceptions revolve around the
ill-conceived notion of p-block, d-block, and f-block elements
... and the corresponding “block structured” periodic table. See
reference 28.
-
Numerous misconceptions concerning absolute zero,
degeneracy, zero-point motion, et cetera.
-
Very often, exercises and quiz questions implicitly require
assuming that
-
Any variable that is mentioned is important.
- Any that is not mentioned must be constant and/or
irrelevant. That is to say, the words “Other Things
Being Equal” (OTBE) are implicitly part of every
question.
An example involves teaching Boyle’s law, Charles’s law, Avogadro’s
law, and Gay-Lussac’s law separately, on the theory that in each case
“the” variables not mentioned are held constant. This is a
notorious OTBE fallacy. For example, T1/P1=T2/P2 is not valid
if we hold N and S constant. See reference 24.
-
Allegedly “Temperature is not a state function.”
(I’m not kidding. A professor vehemently asserted that.)
-
Wild misconceptions about the shape of the H2O
molecule. In fact, contrary to what several chemistry professors
have said:
-
The H2O molecule has a “bent” shape,
more-or-less U-shaped. The stick-figure that approximately
represents the bonds between nuclei is V-shaped, and the
electron-density is U-shaped. See e.g. reference 29.
- The electron density in water does not exhibit tetrahedral
geometry, tetrahedral symmetry, or tetrahedral shape.
Fussing with the terminology will not change these facts. See
reference 29.
-
Attempts to build a classical ball-and-stick model
of the isolated ammonia molecule.
Fact: The isolated gas-phase ammonia molecule in its ground state
has D3h symmetry. See reference 30.
(It has a much lower symmetry, C3v, in liquid
ammonia or in aqueous solution.)
-
You can allegedly determine the temperature of a
flame by looking at its color. (Not just a black body, but a
flame!)
-
Confusion regarding negative temperature coefficient
versus negative activation energy. These are not the same.
-
Persistent failure to understand (even after being told)
that dimensional analysis
can sometimes give the wrong answer, both false positives
and false negatives. That is, arrested development at the
level of dimensional analysis when a scaling analysis is
called for. See reference 31 and
reference 32.
-
Teaching the “density triangle” as described at
e.g. reference 33.
This approach has many weaknesses, but we should not overreact. You
can solve the problem by converting this to an equation M/(D V) = 1
and then forgetting the triangle.
If you don’t convert, and stick with the “cover up” rule, it is not
just opaque to the underlying math, it is actively misleading. The
problem becomes obvious if/when the underlying equation has more than
one variable in the numerator.
The triangle is a crutch. Normal students should not need any such
crutch.
-
Allegedly, the term “algorithmic” is synonymous with rote,
i.e. turning the crank without thinking. This is crazy wrong.
Algorithms are good for you. Do not confuse the presence of one thing
with the absence of another.
-
I once heard a professor talking about a «adiabatic
calorimeter .... “Adiabatic” means no heat.» In other words, we’re
talking about a no-heat heat-capacity experiment. This is what comes
from restricting the definition of “heat” (“flow across a
boundary”) without checking the consequences for consistency.
-
True or False? – There is no such thing as centrifugal
force. See reference 34.
-
True or False? – To model the earth’s magnetic field, take a
globe and skewer it with an ordinary bar magnet, putting the bar’s
“N” pole in northern Canada, and its “S” pole in Antarctica.
-
True or False? – All the dinosaurs died out millions of years ago.
-
True or False? – Yeast consists of microscopic plants.
-
True or False? – If it lays eggs, it’s not a mammal.
4.3 Aviation Misconcsptions
-
True or False? – As part of the recovery from a severe spiral
dive, it is important to roll the wings level and then pull back on
the yoke.
Hint: John-John Kennedy probably didn’t know the right answer to this one.
-
True or False? – The airplane’s stability depends on the fact that the tail is
producing a downward force.
-
True or False? – In a Cessna 172, starting from normal
flight, if you increase the throttle setting (without moving any of
the other controls) the airplane will speed up.
-
True or False? – If two parcels of air flow past a wing, they
move from the front to the back in essentially equal amounts of time,
even if one passes above and the other passes below the wing.
-
True or False? – To work properly, an airplane wing must be
curved on top and relatively flat on the bottom.
-
True or False? – Blowing a jet of air across the top of a piece of
paper is a good way to demonstrate the principle that “faster-moving
air has lower pressure”.
-
True or False? –
Bernoulli’s principle is only valid for incompressible fluids,
which means it cannot be trusted for something as obviously
compressible as air.
-
True or False? – Bernoulli’s principle is essentially a
corollary or application of the principle of conservation of energy.
-
True or False? –
As suggested by the saying “power plus attitude equals
performance”, if you put the airplane into a particular attitude with
a particular power setting, the airplane will give you the
corresponding performance (airspeed, rate of climb, et cetera) and if
you maintain this attitude and power setting you will continue to get
that performance.
-
True or False? –
To perform an ordinary steady roll to the right, the upgoing wing must
produce a greater amount of lift (compared to the other wing), and therefore
a greater amount of drag, which is why you need to apply steady right rudder
during the roll.
-
True or False? – During flight at very low airspeeds, some
sections of the wing are unstalled, while other sections are stalled
and contributing practically nothing to the lift.
-
True or False? – During a normal steady climb, lift is necessarily greater than
weight.
-
True or False? – During a steady, coordinated turn to the
left, dihedral creates a tendency for the airplane to roll back toward
level, and you generally need to apply steady left aileron to overcome
this.
-
True or False? – P-factor (i.e. asymmetric disk loading)
explains why, early in the takeoff roll in a Cessna 172, you must
apply right rudder to keep it going straight.
-
True or False? – On approach, you should never retract the
flaps to correct for undershooting, since that will suddenly decrease
the lift and cause the airplane to sink even more rapidly.
-
True or False? – When properly performing turns on a pylon in the presence of
wind, the airplane will remain at the pivotal altitude, and the
pattern will be shifted somewhat downwind relative to where it would
be in no-wind conditions.
I emphasize that the foregoing list is restricted to misconceptions
that afflict professionals in the field. There is of course a far
wider class of misconceptions that afflict naïve students.
I have seen collections of student misconceptions, but they all seem
so incomplete as to be virtually useless. Furthermore some of them
tend to replace old misconceptions with new ones; see e.g.
reference 4.
5 Next Generation Science Standards
A great many misconceptions are being spread by the NGSS,
as discussed in reference 35.
6 References
-
-
William James,
Talks to Teachers On Psychology; and
to Students on Some of Life’s Ideals (1899).
http://books.google.com/books?id=XYSsCLlF_mkCprintsec=frontcover
Chapter XII deals specifically with memory.
http://ebooks.adelaide.edu.au/j/james/william/talks/chapter12.html -
John Denker,
“How to Deal with Ill-Posed Questions”
www.av8n.com/physics/ill-posed.htm -
John Denker,
“Review of Hewitt, Conceptual Physics
www.av8n.com/physics/hewitt.htm -
John Denker,
“Review of Arons, Teaching Introductory Physics”
www.av8n.com/physics/arons-1996.htm -
P. Hutchison and A. Elby,
“Evidence of epistemological framing in survey question misinterpretation”
AIP Conf. Proc. 1513, 194–197 (2013)
http://dx.doi.org/10.1063/1.4789685 -
John Denker,
“Words Acquire Meaning
from How They Are Used”
www.av8n.com/physics/meaning.htm -
Christopher Horton,
“Student Alternative Conceptions in Chemistry”
http://www.daisley.net/hellevator/misconceptions/misconceptions.pdf -
John Cook and Stephan Lewandowsky,
“The Debunking Handbook”
http://www.skepticalscience.com/docs/Debunking_Handbook.pdf -
John Denker,
“Definition of Weight, Gravitational Force, Gravity, g,
Latitude, et cetera”
www.av8n.com/physics/weight.htm -
Donald E. Simanek,
“Didaktikogenic Physics Misconceptions”
https://www.lhup.edu/~dsimanek/scenario/miscon.htm -
John Denker,
“Weird Terminology”
www.av8n.com/physics/weird-terminology.htm -
John Denker,
“Learning, Remembering, and Thinking”
www.av8n.com/physics/thinking.htm -
John Denker,
“Scientific Methods”
www.av8n.com/physics/scientific-methods.htm -
John Denker,
“Measurements and Uncertainties versus Significant Digits”
www.av8n.com/physics/uncertainty.htm -
John Denker,
“Coherent States”
www.av8n.com/physics/coherent-states.htm -
John Denker,
“Welcome to Spacetime”
www.av8n.com/physics/spacetime-welcome.htm -
John Denker,
“Tabletop Geodesics, General Relativity, and Embedding Diagrams”
www.av8n.com/physics/geodesics.htm -
John Denker
“Expansion of the Universe”
www.av8n.com/physics/expansion-of-the-universe.htm -
John Denker,
“Kirchhoff’s Circuit Laws”
www.av8n.com/physics/kirchhoff-circuit-laws.htm -
John Denker,
“Modern Thermodynamics”
www.av8n.com/physics/thermo-laws.htm -
John Denker,
“Thermodynamics and Differential Forms”
www.av8n.com/physics/thermo-forms.htm -
John Denker,
“Chemical versus Physical Change?”
www.av8n.com/physics/chemical-physical.htm -
John Denker,
“Spontaneity, Reversibility, and Equilibrium”
www.av8n.com/physics/spontaneous.htm -
John Denker,
“Gas Laws”
www.av8n.com/physics/gas-laws.htm -
John Denker,
“How to Draw Molecules ... Just Like Lewis Dot Diagrams,
Only Easier & Better”
www.av8n.com/physics/draw-molecules.htm -
John Denker,
“Balancing Reaction Equations w.r.t Charge and Atoms”
www.av8n.com/physics/balance-charge-atom.htm -
John Denker,
“One Kind of Charge”
www.av8n.com/physics/one-kind-of-charge.htm -
John Denker,
“Periodic Table of the Elements – Cylinder with Bulges”
www.av8n.com/physics/periodic-table.htm -
Martin Chaplin,
“Water Molecule Structure”
http://www.lsbu.ac.uk/water/molecule.html
-
Feynman, Leighton, and Sands
The Feynman Lectures on Physics volume III chapter 9
(“The Ammonia Maser”). -
John Denker,
“Dimensional Analysis”
./dimensional-analysis.htm -
John Denker,
“Scaling Laws”
www.av8n.com/physics/scaling.htm -
Wendy Boomer,
“Density Triangle”
http://westirondequoit.org/ihs/Science/EarthScience/density.htm -
John Denker,
“Motion in a Rotating Frame”
www.av8n.com/physics/rotating-frame.htm -
John Denker,
“Next Generation Science Standards”
www.av8n.com/physics/ngss.htm