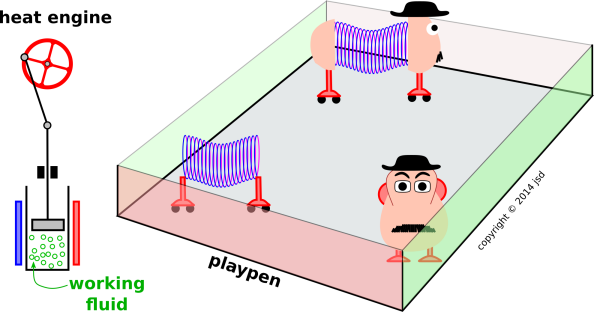
Figure 19.1: Heat Engine versus Slinktato™
In this chapter we consider some basic questions about what can be done with thermodynamics. These include:
We shall see that at most one of these things is possible for any given system. Sometimes neither is possible, but never both. There are actually four scenarios that are worth considering. An overview of the situation can be found in figure 19.1.
Inside the playpen we have three toys: An ideal spring, an ideal heat container (represented by a potato), and a combination of the two (the legendary Slinktato™). Outside the playpen we have a heat engine, and for present purposes we are interested in the thermodynamics of the working fluid within the heat engine.
In more detail:
It is not possible to build a heat engine using a Slinktato™ or anything else you find inside the playpen.
Life would be much simpler if we could just get rid of the notion of “thermal energy content” altogether. This is “almost” but not quite possible. Let’s check the various cases one by one:
The situation is summarized in the following table:
| system: | heat content? | variables? | heat engine? | |||
| spring: | trivial (zero) | too few | no | |||
| potato: | trivial (total) | too few | no | |||
| Slinktato™: | nontrivial | decoupled | no | |||
| heat engine working fluid: | impossible | coupled | yes |
To make it easier to discuss things, we define an uncramped system to be one that has sufficiently many variables and sufficiently few restrictions, so that it could be used as the working fluid in a heat engine. Anything else is considered cramped. In figure 19.1, cramped systems are inside the playpen, while uncramped systems are outside.
There are three main ways of obtaining a cramped system, if that’s what you want:
However, if you are not sufficiently lucky, selective, and/or industrious, it is very likely that a typical system will not be cramped. The relevant variables will not be decoupled.
Furthermore, cramped is not always desirable. If you’re trying to build a heat engine, you want a working fluid that is not cramped.
Often there are timescales that must be considered. For example, if you have a huge current of water in the ocean, the thermal variables are more-or-less decoupled from the mechanical variables on a timescale of days or weeks, but not forever.
Bottom line: Sometimes it makes sense to talk about “heat energy” as something distinct from “mechanical energy” – and sometimes it doesn’t. There is nothing in the laws of physics that makes it certain – or even likely – that such a distinction makes sense. In particular, if you want to use such concepts, it is your responsibility to prove that they make sense, in any given situation.
Let’s look into the situation more carefully, more quantitatively.
| (19.1) |
In such a system, we can have nontrivial thermodynamic cycles.
By the same token, we can consider systems where the T dS term is negligible, and all that remains on the RHS of equation 19.1 is the F·dx term. This corresponds to the spring in figure 19.1.
When there are so few nontrivial variables, you couldn’t draw a thermodynamic cycle if you wanted to. The system is effectively one-dimensional. The notion of “area” on the indicator diagram is undefined and undefinable.
The distinction between cramped and uncramped is indicated in figure 19.2. This is a copy of figure 0.2 as seen in section 0.3.
Remember: The defining property of a cramped system is that it is so constrained that it is not possible to build a heat engine. That means either
As will be explained in a moment, in any uncramped system, there cannot be any notion of “heat content” or “thermal energy content”. To say the same thing the other way, if the system has a well-defined heat-function Q, it cannot be used as the working fluid in a heat engine.
(The converse does not hold; we are not saying that every cramped system has a well-defined Q-function.)
We can begin to understand this as follows: In an uncramped system, you can put energy into the system via TdS heat and take energy out via F·dx work. That’s pretty much the defining property of a heat engine. It guarantees that you cannot define the “thermal energy content” of the system by keeping track of how much heat you put in.
We can formalize this as follows: Suppose there is a Q function, representing thermal energy content, such that Q is a function of state. Consistency with other notions of heat requires that dQ = TdS. Now ∮dQ = 0 since ∮d(anything) = 0 automatically. That means ∮TdS = 0, which makes it impossible to build a heat engine.
We are not saying that the notion of “thermal energy content” is always wrong; we are just saying that it cannot exist in any situation where it is possible to build a heat engine.
Here is another calculation we can do that sheds additional light on the situation. Again suppose that we have
| (19.2) |
Taking the exterior derivative of both sides, we obtain
| (19.3) |
hence
| (19.4) |
since d(d(anything)) = 0. That is equivalent to saying “the boundary of a boundary is zero” as discussed in reference 4. Equation 19.4 can be satisfied if T is constant. It can also be satisfied if the contours of constant T run parallel to the contours of constant S. There are lots of ways this could happen; you could have T ∝ S or T ∝ S2 or whatever. An example is shown in the middle part of figure 19.2.
We can gain additional insight if we expand dT. In accordance with basic principles, we can expand any exterior derivative along the following lines:
| (19.5) |
and plugging into equation 19.4 we obtain
| (19.6) |
The second term on the RHS is obviously zero, so equation 19.4 holds if and only if
| (19.7) |
This equation could hold if dx∧dS = 0, which is the easy way to create a cramped system. However, things are more interesting if we assume this factor is not zero. In that case equation 19.7
| (19.8) |
This equation says in mathematical terms what we said in words back in section 19.1 when we defined the Slinktato™. This is how we arranged for it to have a well-defined heat content.
Now we refer back to the definition of temperature, i.e. equation 7.7, which can be rewritten (subject to mild restrictions) as
| (19.9) |
which means (subject to the assumptions made above) that the system is cramped if and only if
| (19.10) |
Note that if you re-did the calculation to find the conditions under which the integral of work (around a cycle) was zero, you would get
| (19.11) |
which is the same thing, because of the equivalence of mixed partials. We knew in advance that it had to work out this way, because of equation 19.1. The integral of the LHS is zero, so on the RHS, if one term is zero the other must be zero also.
The dichotomy between cramped and uncramped is an endless source of misconceptions.
| People tend to have a great deal of hands-on experience with cramped systems such as the heating and cooling of a potato, or the heating and cooling of a baby bottle. The concepts of energy, temperature, entropy, and heat-content are well defined for such a system. | People have relatively little experience with heat engines. If you generalize from cramped to uncramped thermodynamics, you get to keep the ideas of energy, temperature, and entropy ... but you do not get to keep any notion of heat content or thermal energy content. |
The Slinktato™ is an ultra-simplified example of a compound cramped system.
The ocean is a real-world example. It makes sense to speak of the “thermal energy content” of the ocean. There is also mechanical energy in the ocean, in the form of tides and waves and huge currents such as the Gulf Stream. The mechanical variables are decoupled from the thermal variables to a good approxmation, albeit not exactly. There is a thermodynamic process that drives the Gulf Stream, but virtually none of this energy leaves the ocean in mechanical form, so this doesn’t count as much of a heat engine. There exist tidal stream generators that extract energy from the ocean, but this is a negligible part of the overall energy budget of the ocean. Most of the budget involves purely thermal processes, such as sunlight in and evaporation out.
A lot of people have a knee-jerk response that says “there is no such thing as heat content” but we have to make an exception for compound cramped systems. There is nothing wrong with talking about the “heat content” of the ocean (on an appropriate timescale).
Here is yet another way of looking at the distinction between cramped and uncramped thermodynamics. Consider the elementary example of so-called “heat content” or “thermal energy content” that might arise in connection with a measurement of the heat capacity of a cylinder of compressed gas. We have a problem already, because there are two heat capacities: the heat capacity at constant pressure, and the heat capacity at constant volume. So it is unclear whether the heat content should be CP T or CV T. Now we get to play whack-a-mole: You can remove the ambiguity by rigorously restricting attention to either constant volume or constant pressure … but that restriction makes it impossible to analyze a Carnot-type heat engine.
To repeat: It may at first be tempting to think that the gas cylinder has a so-called “thermal energy” related to T and S, plus a “nonthermal energy” related to P and V, but if you try to build a theory of thermodynamics on this basis you are guaranteed to fail. The sooner you give up, the happier you will be.
Cramped thermodynamics is a legitimate topic. It is only a small subset of thermodynamics, but it’s not crazy. Almost everyone learns about cramped thermodynamics before they learn about uncramped thermodynamics. Consider for example warming the milk in a baby-bottle. This is almost always carried out under conditions of constant pressure. You’re not trying to build a steam engine (or any other kind of engine) out of the thing. In this case, for this narrow purpose, there is a valid notion of the “heat content” of the system.
Within limits, the choice is yours: If you want to do cramped thermodynamics, you can do cramped thermodynamics. Just please don’t imagine your results apply to thermodynamics in general. Cramped thermodynamics by definition is restricted to situations where the state-space is so low-dimensional that there is no hope of building a heat engine or a refrigerator or anything like that. There are no Carnot cycles, nor indeed any other kind of nontrivial cycles.
Long ago, there was a fairly elaborate theory of caloric. This was superseded by thermodynamics during the 19th century.
To repeat, it is OK to talk about “heat content” in the context of warming up a baby bottle. It is OK to talk about “caloric” in connection with a swimming pool as it warms up in the spring and cools down in the fall. It is OK to talk about “thermal energy” in connection with the heat capacity of a chunk of copper in a high-school lab experiment.
However, just because it works in cramped situations doesn’t mean it works in uncramped situations.
It is not OK to talk about “heat content” or “thermal versus nonthermal energy” or “caloric” in the context of uncramped thermodynamics, i.e. in any situation where it is possible to build a heat engine.
Energy is energy. Energy doesn’t recognize the distinction between thermal and nonthermal, and thermodynamics allows us to convert between the two (in any situation where it is possible to have a nontrivial thermodynamic cycle, i.e. in any situation where it is possible in principle to build a heat engine).
The problem is that the Q that appears in equation 19.2 simply cannot exist in the context of uncramped thermodynamics.
The problem still is that Q exists as a state function only within cramped thermodynamics, not more generally, not in any situation where a heat engine is possible. In uncramped thermodynamics, Q may exist as a functional of some path, but not as a function of state.
For a list of constructive suggestions about things that actually do exist as functions of state, see section 8.2.
You can visualize the situation by reference to figure 19.2.
| On the LHS, if we restrict attention to the subspace define by the red line, there is only one path from A to Z. | On the RHS, there are many ways of getting from A to Z, including A→Z, or A→Y→Z, or even paths that include cycles, such as A→X→Y→A→X→Y→A→Z, and so forth. |
| Within the subspace defined by the red line in figure 19.2, you can represent Q as height, and this Q is well defined everywhere in this small, cramped subspace. | You cannot define a Q value as a function of position in a way that is consistent throughout the (T, S) space. The peculiar thing is that you can take almost any simple one-dimensional subspace in the plane and define a consistent Q function there, but you cannot extend this to cover the entire space. You can’t pin down the location of the problem, because it is nowhere in particular, yet it is everywhere: you cannot assign a consistent height to points in this space. |
Pedagogical remarks: Virtually everyone begins the study of thermodynamics by considering cramped situations. This is traditional … but it is a pedagogical disaster for anyone trying to learn uncramped thermodynamics. Cramped thermodynamics is a not a good foundation for learning uncramped thermodynamics; it is aggressively deceptive.
Virtually every newcomer to thermodynamics tries to extend the “heat content” idea from cramped thermodynamics to uncramped thermodynamics. It always almost works … but it never really works.
The next time you feel the need for a measure of “heat content” in the context of uncramped thermodynamics, lie down until the feeling goes away.
Sometimes you hear people talking about “the” reversible from A to B. This makes no sense whatsoever.
The existence of the Carnot cycle A→X→Y→Z→A implies that there are (at least!) two inequivalent paths from A to Z, including the simple path A→Z along a contour of constant entropy, and the more complex path A→X→Y→Z
Furthermore, not all cycles are Carnot cycles. The path A→Y→Z→A is a another perfectly legitimate thermodynamic cycle. Compared to a Carnot-cycle engine, a reversible heat engine that uses the A→Y→Z→A cycle is more complex and harder to analyze, but only slightly so.
Within uncramped thermodynamics, you are allowed to build things that aren’t heat engines. That is, you can have cycles that don’t convert any heat-bath energy into useful work. The various possibilities are summarized in the Venn diagram in figure 19.3, which can be considered a less-detailed version of figure 19.2.
We now focus attention on the immediate neighborhood of point A in figure 19.2. It must be emphasized that paths can depart from point A in innumerably many directions. The Carnot cycle uses only two of these directions (namely the contour of constant T during one part of the cycle, and the contour of constant S during another part of the cycle). However, there are infinitely many non-Carnot cycles, and infinitely many ways in which a reversible path can depart from point A such that neither T nor S is constant. The blue line in figure 19.2 is just one of many such paths.
In the immediate neighborhood of point A, we can distinguish these paths by their direction. The red line in figure 19.2 represents a change in T in the direction of constant S, while the blue line represents a change in T along some other direction.
Therefore, uncramped thermodynamics requires us to treat dT as a vector. If you think of dT as representing some kind of “change in T” you need to specify the direction of the change (as well as the magnitude). Whenever something has a direction and a magnitude, you should suspect that it is a vector.
For large excursions, we would need to specify the entire path, but in the immediate neighborhood of a given point, it suffices to know the magnitude and direction. Therefore a vector such as dT can be considered a function of state. It depends on the local state, not on the entire path. It is a vector-valued function of state.
| The existence of reversible heat engines is sufficient to guarantee the existence of innumerably many inequivalent paths from A to Z, and also to guarantee the existence of innumerably many directions for the vectors located at point A. |
In this chapter, for simplicity, we have not mentioned any
irreversible processes.
Irreversibility is not the cause of the the multiple paths and multiple directions. Conversely, multiple paths and multiple directions are not the cause of irreversibility. |