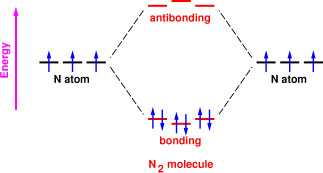
Figure~1: Atomic Orbitals Morph Into Molecular Orbitals
Consider the contrast between chemistry and atomic physics:
| Physics tells us that electrons hate each other. Coulomb’s law. They pair up only as a last resort. This is known as Hund’s Rule #1, or (better) Hund’s Multiplicity Rule (reference~1). (For a rederivation of the idea, see reference~2.) This rule correctly predicts that an isolated nitrogen atom has three unpaired electrons in the valence shell. | Virtually all the chemicals you run into in high-school chemistry have their valence shells filled to the brim with paired-up electrons. The nitrogen molecule has no unpaired electrons. |
So what gives? How do we reconcile these two stories? Why does the rule apply to the N atom but not the N_2 molecule?
We start by noting that the nitrogen atom exists just fine at low density and/or high temperature. In contrast, if you gather nitrogen atoms together at anything remotely resembling STP, they will react violently to form N_2 molecules.
So part of the answer is that chemical species with unpaired valence electrons (called radicals) are usually extremely reactive. High-school chemistry typically omits discussion of anything so violently unstable. Monatomic nitrogen does exist ... but you won’t find it in a bottle in the stockroom.
This leaves us with a refined version of the original question: if electrons hate each other, why do the N atoms sometimes react to form N_2, when they could just remain separate, allowing the electrons to remain unpaired???
Well, the electron-electron repulsion isn’t the only game in town. The atoms don’t dimerize so the electrons can be close to each other; they do it so the electrons can be close to the protons.
So the fundamental answer to the original question is as follows:
| ~~~~~ |
As always, Hund’s Rules apply in the following situation: We start with the independent electron approximation. Then the Rules tell us about effect of electron/electron correlations, which we treat as a correction term.
In monatomic nitrogen, there are three orbitals of equal energy (p_+, p_z, and p_−). We have one electron apiece in each of those orbitals. They have nothing to gain by pairing up: it wouldn’t get them any closer to the nucleus and it wouldn’t lower their kinetic energy. Pairing up is disfavored by the electron-electron repulsion, so it’s not going to happen.
When we have two nitrogen atoms far apart, the story is pretty much the same, simply doubled: we have six orbitals of equal energy, occupied by six electrons, one electron per orbital. All six electrons are unpaired.
However, when the nitrogen atoms get close, things get interesting. We still have six orbitals to play with, but they no longer have equal energy. We say they are “split” by the interaction terms in the Hamiltonian (also called the overlap integral). We wind up with three bonding orbitals and three antibonding orbitals as sketched in figure~1.
Energy-wise, the bonding orbitals are below the antibonding orbitals (and far below the other various places the electrons could go, such as shells with higher principal quantum numbers). So when we try to put our electrons into the lowest-lying orbitals, we have six electrons and three bonding orbitals, so the electrons pair up.
Figure~1 shows this process: we have six atomic orbitals (shown as black lines) when the nitrogen atoms are far apart, and we have six molecular orbitals (shown as red lines) when the atoms are close enough to form a molecule. Electrons are shown as blue arrows. Each electron is shown twice, once in the two-separate-atoms situation and one in the molecular situation.
To repeat the punch line: Two isolated atoms have six electrons to put into six low-lying orbitals, whereas the diatomic molecule has six electrons to put into only three low-lying orbitals.
The molecule still has six orbitals, but the three bonding orbitals are energetically favored because they keep the electrons closer to the nuclei.
Note that we are using the term “orbital” to refer to the spatial part of the wavefunction. The complete wavefunction consists of the spatial part and the spin part. The spin part is discussed in reference~2. We will say just a few words about it here:
If/when electrons decide to share a single orbital, we get pairs (as opposed to, say, triplets) because the electrons have total spin s=½ so there are two possible spin projections s_z={−½ or +½}. If electrons had total spin s=1 then there would be three possible spin projections s_z={−1, 0, or +1} ... and you would find orbitals with three electrons in them. You can’t occupy a given orbital more times than are allowed by the spin multiplicity because of the exclusion principle.
In contrast, if there are two available orbitals at the same energy level, there are two things that happen: First, the electrons will spread out, so that the available orbitals will not be double-occupied more often than necessary. Secondly, they will arrange their spins so as to be aligned (not anti-aligned as they would be if they were paired). The reason for this is explained in reference~2.
Atoms with incomplete non-valence shells (transition metals, rare earths, etc.) can have unpaired electrons in their non-valence shells (in addition to whatever is going on in their valence shells).
The existence of magnetic materials is powerful evidence of unpaired electrons, if you understand what’s going on. The story goes like this: Every electron is a tiny permanent magnet. Every pair of electrons necessarily consists of spin-up paired with spin-down (as required by the exclusion principle). Such a pair produces no net macroscopic magnetism because the two contributions cancel. But in a piece of magnetized iron, for instance, there are lots and lots of unpaired electrons (roughly one electron per atom) all pointing the same direction. The macroscopic magnetic field is just the sum of the contributions from these electrons.
If all electrons were paired, there would be no such thing as ferromagnetism.
For a discussion of why the spatial part of the wavefunction is described by discrete orbitals (rather than a free-for-all), see reference~3. You can get a more-quantitative understanding of where bonding and antibonding orbitals come from by thinking about the H_2+ hydrogen molecular ion, as discussed in reference~4 and reference~5.