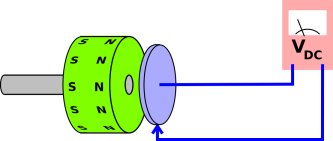
Figure 1: Faraday Rotor Experiment
The Faraday rotor experiment is commonly called “Faraday’s Paradox” or simply “the Faraday paradox” ... but of course it is not really a paradox. It is easily explained in terms of basic notions of circuitry, electromagnetism, and spacetime. It only seems paradoxical if you mis-state the basic laws.
In particular, the experiment shows that 19th-century concepts such as “magnetic field lines” need to be modernized. They work better in four dimensions (not three), and they work better if you think in terms of a unified electromagnetic field, (not separate electric and magnetic fields). Also, this reminds us that the electrostatic rule that says there are no electric fields inside a conductor applies only in the rest frame of the conductor.
Consider the apparatus shown in figure 1. There is a magnetic disk (shown in green) and an electrically-conducting disk (shown in blue). The disk is wired into a circuit with a voltmeter. This includes a rotating slip contact at the center of the disk, and a sliding contact at the edge of the disk.
There are four operational cases to consider. Here are the observed facts:
This experiment, and some interesting variations, are discussed in reference 1.
The result in item 0 is super-easy to understand. This is the trivial, obvious case. The whole situation is static. We can confidently apply Faraday’s law of induction, and thereby predict zero net voltage around the loop. We also use the idea that in a static situation, there are no electric fields inside metal conductors, so not only is there no net voltage, there is no voltage anywhere.
The result in item 1 is almost as easy to understand. Again we apply Faraday’s law of induction. The amount of magnetic flux threading the blue circuit is constant. This is a direct consequence of the symmetry of the rotating magnet, plus the fact that the circuit is a closed loop, and each magnetic field line is a closed loop. We imagine that the field lines are attached to the magnet, so the lines themselves are rotating, but every time one field line rotates out of the circuit, another one rotates in.
To make sense of item 2, we should take a step back and reconsider the rule that says that in electrostatics, there are no electric fields inside a conductor. That’s a fine rule, but there is one proviso: It only applies in the rest frame of the conductor. This makes sense if you think about the microscopic basis of Ohm’s law: the charged particles that carry the current are scattered by impurities and/or phonons in the conductor.
The second step in the analysis depends on the fact that the world is four-dimensional. Hermann Minkowsi invented spacetime in 1908 (reference 2). He said:
| From now on, space of itself and time of itself | |
| shall sink into mere shadows | |
| and only a kind of union of the two | |
| shall maintain its independence. |
In particular, velocity in the x-direction is the same as a rotation-angle in the xt plane. For present purposes, we need a slightly different (yet inimately related) idea:
| From now on, the electric field and the magnetic field | |
| shall sink into mere shadows | |
| and only a kind of union of the two | |
| shall maintain its independence. |
In particular, an electromagnetic field that looks purely magnetic in one frame will be partly electric in another frame. Conversely, an electromagnetic field that looks purely electric in one frame will look partly magnetic in another. This is indicated in the spacetime diagram in figure 2 and explained in reference 3.
So: At each point in the rotating disk, let us choose a reference frame that is instantaneously comoving with the disk. In this frame, there is no electric field. In this frame, the field is purely magnetic. If there were an electric field, the mobile charged particles would move in accordance with Ohm’s law, and would keep moving until they canceled the electric field.
However, when we transform back to the lab frame, the field is no longer purely magnetic. There will be an electric field, aligned with the radial direction of the disk. This is required by special relativity. This is what happens when you rotate a magnetic field in the xt plane.
As before, we can apply Faraday’s law of induction to conclude that there is no net voltage drop around the circuit. However, that does not mean that there is no voltage anywhere. There is in fact a voltage drop from the center of the disk to the edge. There will be an equal-and-opposite voltage drop across the voltmeter.
We can analyze item 3 in the same way. It doesn’t matter whether the external field applied to the disk is purely magnetic or contains an electric component. It doesn’t matter whether the magnetic field is rotating or not. All we need to know is the rule that says the mobile charged particles will move so as to null out the electric field inside the conductor ... in the frame comoving with the conductor. In this frame, the field will be purely magnetic.
When we transform back to the lab frame, there is a radial electric field in the disk, and the voltmeter measures this.
This is a prime example of the sort of mistake that leads to so-called paradoxes.
We know from other considerations that the magnetic field does move along with the magnet, to a first approximation. This is obvious if you just take a bar magnet and throw it.
You can create a pseudo-paradox here by assuming that the magnetic field does not rotate when the magnet rotates. This sufficies to explain the results of the experiment as discussed in section 1.
This is however problematic, for the following reason: Suppose the rotating magnet is slightly imperfect at one point. The “extra” magnetic field due to the imperfect obvious will rotate with the magnet. It is then hard to understand why the rest of the magnetic field would not rotate.
An even worse problem is that this is inconsistent with other things we know about moving magnetic fields, such as the microscopic origins of the magnetic field of a long straight wire, as discussed in reference 4.