16  Adiabatic Processes

16.1  Various Definitions of “Adiabatic”

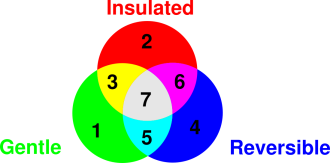
The word adiabatic is another term that suffers from multiple inconsistent meanings. The situation is summarized in figure 16.1. The underlined terms capture some of the possible meanings of adiabatic.

Figure 16.1: Some Concepts Related to Adiabatic

a) Some thoughtful experts use the term adiabatic to denote a process where no entropy is transferred across the boundary of the region of interest. In other words, the system is thermally insulated. This was probably the original meaning, according to several lines of evidence, including the Greek etymology: α + δια + βατoς = not passing across. This implies that the process must be fast enough so that the inevitable small heat leaks are insignificant. As a corollary, we conclude the entropy of the region does not decrease. This is represented by regions 2, 3, 6, and 7 in the diagram.

b) Other thoughtful experts use the term adiabatic approximation (in contrast to the sudden approximation) to describe a transformation carried out sufficiently gently that each initial state can be identified with a corresponding final state, and the probabilities (aka occupation numbers) are not changed – at least not changed by the transformation process itself.

c) Dictionaries and textbooks commonly define “adiabatic” to mean no flow of entropy across the boundary and no creation of entropy. This is represented by regions 6 and 7 in the diagram. As a corollary, this implies that the system is isentropic. That is to say, its entropy is not changing.

Here are some illustrations of the relationships between the various definitions:

• As an example where definition (a) applies, but definition (c) does not, see reference 47. It speaks of an irreversible adiabatic process. That means the system is thermally insulated, but entropy is being created deep within the interior of the system. This is represented by regions 2 and 3 in the figure.

  To say the same thing the other way: In the dream-world where only reversible processes need be considered, definitions (a) and (c) would be equivalent, but that’s not much help to us in the real world.

  (In contrast, if we were discussing energy, the ideas of “no flow across the boundary” and “no change” would be equivalent, since energy can never be created or destroyed.)

• As an example where definition (b) applies but definition (a) might or might not, consider the refrigeration technique known as adiabatic demagnetization. The demagnetization is carried out gently, so that the notion of corresponding states applies to it – or at least it would, if the system were isolated. It would cause the temperature of the spin system to decrease.

  The interesting thing is that people still call it “adiabatic” demagnetization, to indicate gentleness, even when the system is not insulated, i.e. when definition (a) does not apply. Specifically, consider the subcase where there is a steady flow of heat inward across the boundary of the system, balanced by a steady demagnetization, so as to maintain constant temperature. Lots of entropy is flowing across the boundary, violating the first definition, but it is still called adiabatic demagnetization in accordance with the second definition. This subcase is represented by regions 1 and 5 in the diagram.

• As an example where all three definitions would apply, but only definition (b) is intended, consider the magnetic resonance technique known as “adiabatic fast passage” or “rapid adiabatic passage”. The word “adiabatic” in this context means the process is slow and gentle enough that there will be corresponding states, and occupation numbers will be preserved. Meanwhile, in this context the notion of no entropy flow across the boundary is not implied by the word “adiabatic”, so the word “fast” is used to indicate that not much entropy flows across the boundary in the available time. To repeat: adiabatic fast passage involves both ideas: it must be both “fast enough” and “slow enough”. This example sits in region 7 in the diagram.
• It is possible to have a transformation that is isentropic but does not produce states with corresponding probabilities. This is illustrated by figure 16.2. The red probability distribution and the blue probability distribution have the same entropy, namely 2 bits. However, there is no way to match red states with blue states of the same probability. This should be clear from the fact that two of the red states have exactly the same probability, whereas no two blue states do. Also, you can see that the lowest two red states cannot be matched with any blue state of the same probability, not even close.
  
  Figure 16.2: Non-Corresponding Probabilities

  We can arbitrarily identify certain states as “corresponding” according to their identification number, 1 though 11, but the entropy doesn’t care about that. It only cares about the probabilities.

  For another example where there are corresponding state ID numbers, but the probability of each state might or might not be preserved, see section 16.2.

• Although a reversible insulated system must be isentropic, the converse does not hold. Consider for example a metal wire with one end connected to a hot heat bath, and the other end connected to a cold heat bath. In the steady state, the entropy of the wire is not changing. The entropy just flows through without accumulating.

My recommendation is to avoid using the term adiabatic whenever possible. Some constructive suggestions include:

• If you mean thermally insulated, say thermally insulated.
• If you mean a non-sudden perturbation, say non-sudden or gentle.
• If you mean isentropic, say isentropic.
• Instead of the nouns “adiabat” or “adiabatic line”, say “contour of constant entropy”.

16.2  Adiabatic versus Isothermal Expansion

Suppose we have some gas in a cylinder with a piston, and we gradually move the piston so that the gas expands to twice its original volume.

Further suppose that we do this fast enough that there is no thermal energy transport through the walls of the cylinder ... yet slow enough that there is a 1-to-1 correspondence between the states before and after. So this is adiabatic in every sense of the word. The process is diagrammed in figure 16.3.

Figure 16.3: Isentropic Expansion

We consider 20 states, as shown by the dots in the diagram. These are, for practical purposes, the only accessible states. That is to say, all the higher-energy states are unoccupied, to a good approximation. In the diagram, there are three panels. The left panel shows the situation before expansion, and the right panel shows the situation after. The middle panel is a “energy level diagram” that shows how the energy of each mode changes during the expansion.

You can see that within each pair of corresponding dots, the probability is the same before and after. Therefore the entropy of the gas is exactly the same. The energy of the gas has gone down, and the temperature has gone down in equal measure. The slope of the red line is an indication of temperature, in accordance with the Boltzmann factor.

We can contrast this with the isothermal expansion shown in figure 16.4. The gas in this case is in contact with a heat bath, so that during the expansion the temperature does not decrease. The energy of each mode goes down as before, but the occupation numbers do not stay the same. The lion’s share of the probability is now distributed over twice as many states. Therefore the entropy of the gas goes up. Within each pair of corresponding states, each state is very nearly half as likely after, as compared to before.

Figure 16.4: Isothermal Expansion

The red line is shifted to the right by one unit, reflecting the 2× lower probability of each state, but it keeps the same slope, representing the constant temperature.