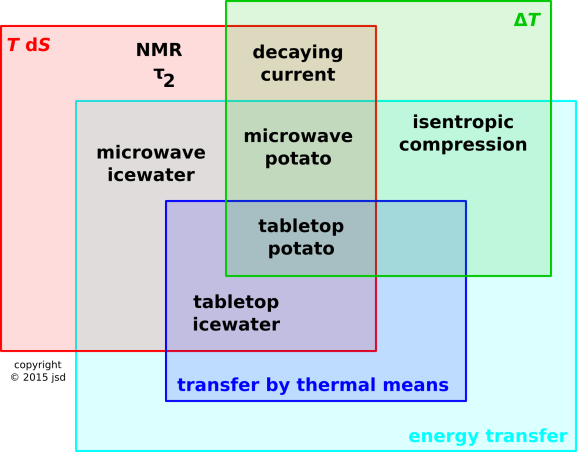
Figure 17.1: Heat: Multiple Definitions, Multiple Examples
The term “heat” is a confusing chimera. It is partly energy, partly entropy, partly temperature, and partly who-knows-what. It shows up in a variety of idiomatic expressions, some of which are useful, as discussed in section 17.2. However “heat” by itself is not particularly useful.
By itself, the word “heat” has at least six reasonable and widely-used but mutually-inconsistent technical meanings, as enumerated below. In addition there are innumerable nontechnical, metaphorical, jocular, and/or not-so-reasonable meanings. It is not worth arguing about the relative merits of these meanings, except to say that each has some merit. I observe that a typical thoughtful expert will use each of these meanings, depending on context. It would be nice to have a single, universally-accepted meaning, but I doubt that will happen anytime soon.
In some cases you can figure out the meaning from context. In other cases it is better to avoid the term “heat” altogether, and quantify something else instead (perhaps temperature, energy, and/or entropy).
Here are some of the relatively-sensible technical definitions of “heat”. Studying this list in detail is not worthwhile, but you should skim it, just to get some appreciation for how much trouble you get into when you try to define “heat”:
This type of heat is extensive, in the sense that if you build twice as many heat engines and operate them all in the same way, you get twice as much TdS.
For any given path Γ, this heat is a scalar with dimensions of energy. However, it is very sensitive to how you choose the path, so it might be better to think of it as a functional of the path, as discussed in item 4. The overall functional f[] is distinct from the specific scalar f[Γ].
When we consider the various paths Γ from state A to state B, the heat is not a function of state (h(B) for all B) or even a function of the two states (h(A, B) for all A and B), but rather a functional depending on every detail of the path (h[Γ] for all Γ). See chapter 7 for a discussion of functions of state. See reference 48 for the definition of functional. We write h[⋯] with square brackets to emphasize that it is a functional, not a mere function.
This heat is a mapping from paths to scalars. Thinking of it as a mapping highlights the connection with item 2, insofar as a one-form is a mapping from vectors to scalars.
In the narrow set of situations where the concept makes sense, it goes by various names including heat content, aka thermal energy, aka caloric, aka Q. An example of this is discussed in section 11.5.3. This is an extensive scalar, and can be measured in joules. Beware that this notion cannot be extended to uncramped thermodynamics. It cannot even be safely extended from one cramped situation to another, as you can see from the fact that ΔQ=CVΔT is different from ΔQ=CPΔT ... yet each is called “heat” within its own cramped subspace (constant V or constant P respectively).
In addition, one sometimes encounters some less-than-reasonable definitions, including:
You have to be careful, though, because even though heat usually is connected to enthalpy (as in the heat capacity CP), sometimes it is connected to energy instead. For example, as discussed in section 7.5, the heat capacity CP measures enthalpy per unit temperature, whereas the heat capacity CV measures energy per unit temperature. The fact that both are called the “heat” capacity makes it impossible to assign an unambiguous meaning to “heat”.
As an example where definition #1 and definition #2 apply, but definition #5 does not, consider the notion that a microwave oven heats a potato. Clearly (1) the food gets hotter. Clearly (2) the entropy of the food changes. However, (5) no entropy was transferred across the boundary of the food. Energy was transferred, but the entropy was created from scratch, within the food. According to any reasonable definition of temperature, the microwave-generating components inside the oven aren’t very hot, so you can’t say the energy was transferred “as the result of a difference in temperature”. This is one of the examples shown in the Venn diagram in figure 17.1.
As an even more spectacular example, consider a system consisting of a closed loop of wire. At time t=0 there is a current flowing in the wire. This current is decaying, on a timescale given by L/R. The entropy and temperature of the wire are increasing, even though no energy is being transferred (thermally or otherwise) across the boundary of the system. NMR τ1 processes are in the same category.
The distinction between (2) and (5) is an instance of the boundary/interior issue, as discussed in section 8.6.
As an example where definition #2 and definition #5 apply, but definition #1 does not, consider a glass of ice water sitting on the table. We say that heat leaks into the system and melts the ice. The temperature does not change during the process.
As an example where definition #2 applis, but definition #5 and definition #1 do not, consider a glass of ice water in the microwave oven. The ice melts, but the temperature does not change, and no energy was tranferred in thermal form across the boundary.
As an even more spectacular example, consider the NMR τ2 process. Entropy is increasing, even though no energy whatsoever is being transferred (thermally or otherwise).
As an example where definition #1 applies but definition #2 and definition #5 do not, consider the reversible thermally-insulated compression of a parcel of gas. We say the gas heats up, and arguably one could say there is an increase in the amount of “thermal energy” within the region. On the other hand, clearly no heat or entropy was transferred across the boundary, and there was no change in the entropy within the region. I have seen experts refer to this as adiabatic heating; this makes perfect sense in context, but comes as a shock to anyone who thinks definition #5 is the only definition.
We now discuss in more detail the advantages and disadvantages of definition #5:
| Definition #5 is the most prevalent, perhaps in part because it is easily expressed in non-mathematical words. Many students have been forced to learn this definition by rote. | Rote learning is a poor substitute for understanding. |
| Definition #5 makes sense in some situations, such as a simple non-moving heat exchanger in a non-dissipative system. | Such situations are not representative of the general case. |
| Definition #5 focuses attention on flow across a boundary. This is good, because we believe all the laws of physics should be stated in local form, and flows across a boundary are crucial for this. | It focuses on temperature and heat. It would be better to focus on energy and entropy. Certainly energy and entropy can flow between systems that don’t even have a well-defined temperature (let alone a difference in temperature). Also remember that heat is not a conserved quantity, and it is hard to know what “flow” means when applied to non-conserved quantities. Whenever you talk about heat flow, you run the risk that non-experts will visualize heat as some sort of conserved fluid. |
Heat is non-conserved twice over. First of all, even in reversible processes, heat is non-conserved because non-Locrian energy can be converted to Locrian energy and (within limits) vice versa. As mentioned in section 11.5.7 energy is conserved, but heat (by itself) is not conserved. Secondly, in irreversible processes heat is not conserved because entropy is not conserved.
The word “heat” occurs in a great number of idiomatic expressions.
As is always the case with idiomatic expressions, the meaning of the expression as a whole cannot be inferred from the meaning of the individual words. In particular, most of the following heat-related idiomatic expressions are reasonably well defined, even though the word “heat” by itself is not:
At the next level of detail, here are some notes on the last three items:
As a related point of terminology: Keep in mind that the symbol H conventionally stands for enthalpy; it does not stand for heat. Alas, many texts don’t distinguish between heat and enthalpy. That’s a problem because sometimes the enthalpy of reaction (δH) shows up as heat, and sometimes as something else (such as electrical energy).
If you mean hotness, as in definition #1 above, it is better to speak of temperature rather than heat. This avoids an ambiguous use of the term “heat”.
When experts talk about the T dS vector (definition #2) they commonly call it literally T dS (pronounced literally “tee dee ess”). This is nicely unambiguous. The term “heat vector” is a slightly more elegant way of talking about the same idea. The point is that saying “heat vector” rather than merely “heat” makes it clear we are talking about T dS, thereby removing a great deal of ambiguity. Remember that this vector is a one-form (as opposed to a pointy vector), and lives in abstract thermodynamic state-space (unlike everyday position vectors). The RHS of figure 8.4 shows you how to visualize the T dS vector. For an introduction to one-forms and how they apply to thermodynamics, see reference 4.
In almost all cases where the “transfer across a boundary” idea is used (definition #5), the T dS vector idea (definition #2) would be a more precise and more reliable way of describing what is going on. This removes the inconsistencies associated with the “transfer across a boundary” idea. Also, whether or not energy is being transferred across a boundary, visualizing T dS as a vector resolves a goodly number of conceptual problems.
Here is a helpful analogy:
| The problematic concept of phlogiston was replaced by two precise concepts (namely oxygen and energy). | The problematic concept of heat has been replaced by two precise concepts (namely energy and entropy). |
As another analogy, consider the comparison between “heat” and “blue”, another common four-letter word.
| Nobody in his right mind would try to quantify what “blue” means. Instead of quantifying the blueness, you should quantify something else, perhaps power versus wavelength. | Instead of quantifying heat, you should quantify the energy and entropy. |
Actually “heat” is far more problematic than “blue”, because there’s something even worse than imprecision, namely holy wars between the Big-Endians and the Little-Endians, each of whom think they know “the one true definition” of what “heat” is.