Figure 1: Two Clocks – Consistency Required
The usual statement of this puzzle goes something like this: There are two twins, Joe and Moe. When we first meet them, they have the same age, as we naturally expect for twins.
Joe stays at home, at rest, while Moe goes on a trip. He travels outbound at nearly the speed of light, then turns around and comes back at nearly the speed of light.
The interesting bit is that when the twins meet up at the end of the trip, Moe is younger than Joe — younger according to the clocks he carries, younger according to biological aging processes, younger in every way. Our task is to find the best way to understand this situation, qualitatively and quantitatively.
Mnemonic: Moe is the one with multiple motions, while Joe travels in a simple straight line through spacetime.
Before analyzing this puzzle, there is an important philosophical and pedagogical point to be made: So-called “paradoxes” only arise if/when somebody mis-states the laws of physics. The mis-stated laws of physics are full of paradoxes. The correctly-stated laws of physics are not. (There may be some situations where we don’t know the correct laws of physics, but this isn’t one of them. Timekeeping for traveling twins is very well understood.)
A paradox-free explanation of relativity is presented in reference 1. Using paradoxes to teach relativity is abhorrent, although (alas) common. By way of analogy: I could come up with a dozen “paradoxes” in elementary nonrelativistic mechanics, but it would be terrible pedagogy to inflict them on students who are trying to learn elementary mechanics.
Devising “paradoxes” easy; you just need to trick people into mis-stating the problem. This sort of trickery is not helpful, especially in an introductory course.
Our goal is to get to the point where we can say there is no paradox from either twin’s point of view.
Each and every object moves along its own world line at the rate of 60 minutes per hour.
A clock has the additional property that it puts tick marks on its world line as it goes along. Each tick mark is a spacetime event, meaning it occurs at a definite point in (t, x, y, z) space. The clock ticks along at a steady rate, so the tick marks are evenly spaced in spacetime, and normally the spacing is precisely calibrated according to some standard. This is what clocks do.
If you are moving relative to the clock, or if the clock is moving relative to you, the clock doesn’t care. The clock is not moving relative to itself. The clock measures its own proper time and puts tick marks on its own world line. If your world line is different from the clock’s world line, that’s not the clock’s problem.
The simplest way to analyze a clock is to analyze it in a frame comoving with the clock. (After having done that, you can then, if you want, figure out how the tick marks look in other frames. See reference 2 for an analysis of a few types of clocks.)
Sometimes people imagine that certain types of clocks slow down when they are in motion relative to the lab frame ... while other clocks do not. This is a horrific misconception. Think about the consequences: According to a nonmoving observer, we have two clocks that agree, putting the same marks on the world line. However, according to an observer moving relative to the clocks, the same two clocks disagree, putting incompatible marks on the world line. You can’t have it both ways; either the marks agree or they don’t. All observers see the same marks, so you can’t argue that one observer sees agreement while another doesn’t.
This is relevant to the twins puzzle, because it means that “time” as defined by biological aging is the same as “time” defined by atomic clocks, laser resonators, mass-on-a-spring oscillators, or whatever.
Let’s be clear: You cannot resolve the so-called paradox of the twins by imagining that aging-time is different from clock-time. Time is just time. The tick marks on the world line exist independently of whether they are being observed by this-or-that moving observer.
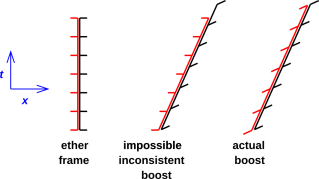
This point is tremendously important for the conceptual foundations of physics. Suppose we have two different kinds of clocks sitting side by side, as shown in figure 1, where one clock is represented in red and the other is represented in black. Now imagine what would happen if the black clock (perhaps a laser clock) were subject to the laws of relativity, while the red clock (perhaps a biological clock) was not. Then by comparing the two clocks, you could tell whether you were moving relative to the “ether”. This is shown in the middle part of figure 1. That is, you could detect absolute motion. This would be very shocking. It would would overthrow the fundamental principle of relativity, which goes back to Galileo, namely the principle that there is no way to detect or even define absolute motion, since a closed system in uniform motion behaves exactly the same as a system at rest.
All clocks must behave the same. The clocks do not know and do not care which (if any) moving observers are looking at them. Over the last 300+ years, physicists have made numerous careful attempts to detect absolute motion. There is no evidence that any such thing exists. Any discrepancy between one type of clock and another must be exceedingly small, or it would have been detected long ago.
To understand what really happens to the twins, it is tremendously helpful to diagram the situation, using spacetime diagrams.
Note: If you want to make your own spacetime diagrams, you may find it convenient to start with prefabricated spacetime graph paper. Then all you have to do is add the events. You can print your own spacetime graph paper from the files in reference 3.
The story of the twins can be analyzed using figure 2, figure 3, and figure 4.
In figure 2, we depict in green a reference frame comoving with Joe, the stay-at-home twin. The solid green lines are parallel to the green observer’s t axis, i.e. they are lines of constant xg. Similarly the dashed green lines are parallel to the green observer’s x axis, i.e. they are lines of constant tg.
In figure 3, we depict the reference frame of the red observer, who is comoving with Moe during the outbound part of the trip. The solid red lines are parallel to the red observer’s t axis, i.e. they are lines of constant xr. Similarly the dashed red lines are parallel to the red observer’s x axis, i.e. they are lines of constant tr.
In figure 4, we depict the reference frame of the blue observer, who is comoving with Moe during the inbound part of the trip. The solid blue lines are parallel to the blue observer’s t axis, i.e. they are lines of constant xb. Similarly the dashed blue lines are parallel to the blue observer’s x axis, i.e. they are lines of constant tb.
In each of the three figures, the dotted black line is irrelevant to this problem. It’s just for fun. It’s the world-line of a photon. It shows that all observers agree that the photon is lightlike, i.e. it moves right down the diagonal of the unit “squares” in all frames. (Note that the unit “squares” of the red and green observers look like rhombi in the diagram, because the diagram is drawn in the lab frame. The green observer is at rest in the lab frame, while the red and blue observers are not.
In all three figures, Moe’s path is marked with a heavy line, red for outbound and blue for inbound. The turnaround point is circled.
The red observer synchronizes his watch to the green observer at the event where they pass each other (point A in the diagram). The blue observer sets his watch so that it will be synchronized with the red observer’s at the point where blue and red pass each other, i.e. the turnaround point. Note that the idea of “synchronization” is well defined if-and-only-if the parties are colocated.
Let’s check on things at the moment when Moe reaches point b. Moe, using his own notion of what “now” means, i.e. using the red contours of constant time, asks himself what the “current” time is back home. He concludes that Joe has just reached point B. If we compare Moe’s age at b with Joe’s age at B, we find that Joe is younger at this stage of the game (but the game is not over).
Let’s perform the same check at point c. Since Moe is now on the inbound leg of the journey, his notion of “current” time is defined by the blue contours of constant time. He concludes that Joe has just reached point C. If we compare Moe’s age at c with Joe’s age at C, we find that Joe is older.
Something very special happened during the turnaround. According to Moe, very little time passed between b and c, even though Joe’s age increased significantly between B and C.
Again we emphasize that nothing funny happened to Moe’s clocks or Joe’s clocks. The main thing that changed between b and c is that Moe changed his notion of what “now” means at distant places. This is an example of the breakdown of simultaneity at a distance.
Note that we do not need to worry about what Gee forces Moe is subjected to during the turnaround. The forces don’t matter. Here we see one of the great virtues of the “instantaneously comoving” reference frames: we imagine that long ago, Moe’s friends put into place (and put into motion) a whole ensemble of reference frames, so that whenever Moe needs to, he can reach out and grab an instantaneously comoving frame. These frames are not accelerating, so there is no question of their clocks being damaged by acceleration.
No matter how Moe accomplishes the turnaround, the coordinate system he uses for the inbound leg will necessarily be strongly tilted (in spacetime) relative to the one he used on the outbound leg. In the figure, you can see that the blue contours of constant time are tilted relative to the red contours of constant time. This tilt will produce a huge change in Moe’s notion of what is the “current” time back home.
The question of whose clock is “fast” and/or whose clock is “slow” would be difficult to answer, but fortunately it need not be asked. Instead, we focus on questions that can be unambiguously answered, such as Moe’s questions about Joe’s age at points B and C.
Moe knows that Joe’s clocks are doing the right thing, namely placing properly-spaced tick marks along Joe’s world line. Similarly, Joe knows that Moe’s clocks are doing the right thing, namely placing properly-spaced tick marks along Moe’s world line.
Moe doesn’t say that Joe’s clocks are running slow; it is much better to observe simply that Joe’s world line crosses Moe’s contours of constant time at a funny angle.
Figure 5 shows all three reference frames at once. The figure is a bit “busy” and most of the main ideas could be explained using simpler diagrams, one frame at a time, so we postponed showing the combined diagram. However there remains one point that needs to be made: As shown in figure 5, all three views of the situation are consistent. There is an underlying objective reality to spacetime. That is, an event has physical and geometrical reality, no matter which observers, if any, are observing it.
Different observers may represent a given event using different components, but it’s still the same event. For more on this, see reference 4.
There is a profound analogy between ordinary spacelike rotations (change of angle) and boosts (change of velocity). A boost mixes x and t in much the same way as an ordinary rotation mixes x and y.
The main difference is that spacelike rotations are circular (involving sin() and cos() functions), while boosts are hyperbolic (involving sinh() and cosh() functions).
We can construct a spatial analogy to the twins puzzle. Suppose Joe walks from A via B and C to D, more-or-less as depicted in figure 2. Meanwhile, Moe walks from A via b and c to D. We ask how many steps it takes to go from A to D. Well, that depends. Joe took the direct route, while Moe to the scenic route, so Moe required more steps.
The main difference is that in the spatial case, the scenic route always requires more steps than the direct route (assuming the terrain is flat), while in spacetime, the hyperbolic geometry means that the scenic route always requires less proper time than the direct route (under mild assumptions).
In any case, the main part of the analogy is clear: Moe and Joe shake hands at A, which is an event in spacetime, denoting a definite place and a definite time. Later they shake hands at D, which is another event in spacetime, another definite place and time. Moe reaches D having traveled a longer distance according to his pedometer, and having traveled a shorter time according to his clock.
In the non-relativistic limit, the notion of “elapsed time from A to B” is well defined, and is the same for all observers ... but in general, i.e. if some observers are moving at relativistic speeds, then the elapsed time is just as path-dependent as the mileage.
In this section I will – very temporarily – not follow the advice about paradoxes given in section 1.2. Adhering to convention rather than good sense, I will present a pseudo-analysis which makes it seem that there is a paradox. You are warned that the indented paragraphs are said with tongue in cheek and fingers crossed, and are not to be taken seriously.
Joe predicts that Moe will age very little during the trip, according to the “conventional” idea that a clock that is moving relative to Joe will run slow relative to Joe’s clock. At the end of the trip, when the twins are reunited, Moe will be nearly two years younger than Joe.
Meanwhile, at every moment during the outbound trip, Moe can do the same calculation in reverse. Moe says that Joe is moving, and therefore Joe’s clocks should be running slowly compared to Moe’s. Similarly, Moe says that during the return trip, Joe’s clocks are again running slow.
This is a paradox. We cannot have each guy’s clock be slower than the other.
This “conventional” analysis has multiple deficiencies. One nasty trick is that although we discussed both the outbound leg and the inbound leg of Moe’s trip, we failed to discuss what happens in the turnaround region, where he switches from outbound to inbound motion. This is a critical omission, as will be discussed below.
Another bit of dirty dealing has to do with the notion that “moving clocks run slow”. Non-experts sometime labor under the impression that “moving clocks run slow” is one of the axioms – or at least one of the theorems – of relativity. It’s not. At best it describes only part of what happens, and even then it gives an approximate and somewhat misleading description.
Here is another argument made with tongue in cheek and fingers crossed. The following indented argument is not to be taken seriously:
Joe sees Moe fly away and return younger. But the situation is symmetric, since we cannot detect absolute motion. Therefore it is equally true that Moe sees Joe fly away and return. So Moe thinks Joe should be younger. This is a paradox; they cannot each be younger than the other.
This argument is invalid. Although we cannot detect (or even define) absolute velocity, we certainly can define and detect absolute acceleration. Moe undergoes acceleration, and everybody knows it. Joe remains at rest, and everybody knows it. The situation is not symmetric.
The basic laws of motion (in their usual form) only apply in an unaccelerated frame. Similarly, the laws of special relativity (in their usual, basic form) only apply in an unaccelerated frame. Fortunately, that doesn’t prevent us from figuring out what an accelerated observer will see. We simply apply the basic laws in an unaccelerated frame, and see what that implies about the accelerated frame. For example, we find that in a rotating frame, the basic laws must be supplemented by centrifugal effects and Coriolis effects, as discussed in reference 5. Analogously, during the turnaround, Moe’s equations for time at distant places must be heavily corrected because of the acceleration Moe is undergoing.
Remember, the procedure is to use Special Relativity (in nearby unaccelerated frames) to figure out exactly what the corrections must be. When in doubt, ask how things would look to an instantaneously comoving unaccelerated observer. There are lots and lots of problems for which this method is useful.
Some people imagine that you need General Relativity to handle accelerated observers – but you don’t. General Relativity has to do with gravitation, and with curved spacetime. The centrifugal field on a playground merry-go-round is not caused by spacetime curvature, and similarly the time-shift that Moe sees during the turnaround is not caused by spacetime curvature. Using GR to solve such problems would be like using a gold-plated jackhammer to crack open a pistachio. It would work, but it would be more machinery than is really needed.
You do not need GR to help you solve the twins puzzle, and in fact it’s just the other way around: understanding how Special Relativity deals with the twins puzzle is a prerequisite to understanding GR.
The way to fool people about the twins puzzle is to emphasize the alleged symmetry: At any moment of time, one twin is moving relative to the other, and according to the laws of Special Relativity, you can arbitrarily choose either one of them to be “your” reference frame, so the situation seems symmetric. Using the word “twins” reinforces the idea of symmetry. But what’s true at any particular moment isn’t true overall. Special Relativity says you can choose any one unaccelerated reference frame as “your” reference frame. Joe has a reference frame, but Moe, alas, has at least two: one outbound and one inbound. We can make the frame-independent statement that Moe’s two frames are moving relative to each other. That’s all that need be said to break the symmetry: Moe undergoes acceleration while Joe does not, and that makes all the difference. Special Relativity has no problem saying that.
Consider the following analogy:
| It would be unwise to say that a ruler gets shorter if we look at it nearly end-on. It’s OK to say that the projection of the ruler on our field of view is shorter, or perhaps that the appearance of the ruler is foreshortened – but there has been no real change in what the ruler is. | It would be unwise to say that a clock runs slowly if we are moving relative to it. The clock doesn’t know or care whether we are moving. It’s OK to say that the projection of the clock’s world line onto our field of view projects tick marks that are more widely spaced, but there has been no real change in what the clock is or what it does. |
If you want to defend the idea the moving clocks run slow, you ought to start by defending the idea that rulers get shorter if viewed nearly end-on. If you want to be logically consistent, you can’t have one without the other.
I’m not talking about Lorentz contraction here; I’m talking about plain old rotation. Note that the rotation group is a subgroup of the Lorentz group.
Most people consider it obvious that the proper length of a ruler is independent of the viewing angle.
The rotational analog of the twins “paradox” makes the “paradoxical” claim that an ordinary one-foot ruler is less than an inch long, allegedly because I can arrange two rulers end-to-end in a narrow V shape, with the starting point of the first ruler only one inch from the ending point of the second ruler. This V shape is closely analogous to the traveling twin’s V-shaped world line, as shown in figure 2.
I put “paradox” in scare quotes, because it’s not really a paradox; it’s just silly. The rulers are being used improperly.
There is a profound analogy between rotations and boosts. Viewing a ruler end-on doesn’t change what the ruler is. Similarly viewing a clock from some boosted reference frame doesn’t change what the clock is or does.
The projection of the clock or ruler onto your field of view will depend on your viewpoint, but that is a property of the projection, not a property of the clock or ruler.
When the two twins rejoin each other at point D, Moe will be younger. This will be true no matter how you measure it, whether by biological aging processes, or by the number of tick marks placed on the world lines by properly-calibrated clocks of whatever type.
This emphatically does not mean that Moe’s clock ran slow or that Joe’s clock ran fast. Each clock did the right thing all along. Each clock laid down properly-calibrated evenly-spaced tick marks on its world line.
For more on the geometry and trigonometry of spacetime, and the importance of invariant time and invariant length, see reference 6.
Several people have asked me about the fact that elementary particles (e.g. muons) are observed to decay more slowly when they are in motion relative to the lab frame. Doesn’t that mean that the muon’s on-board clock is running slow? No, it doesn’t.
Consider another spatial analogy. Our heroes, the twins Moe and Joe, drive from point A to point D in separate cars. Each car has an odometer and a clock.
Do we conclude from this that Moe’s odometer is somehow broken, and measures some sort of weird “contracted” miles? Of course not. A far simpler explanation is that Moe took the scenic route, while Joe took the direct route.
In the non-relativistic case, we find that even though the odometers give a path-dependent notion of elapsed distance, the clocks give a path-independent notion of elapsed time.
The only halfway-tricky thing about relativity is that if the twins travel at high speeds, their clock readings become just as path-dependent as their odometer readings.
Do we conclude from this that Moe’s clock is somehow broken, and measures some sort of weird “slow” seconds? Of course not. A far simpler explanation is that Moe took the scenic route, while Joe took the direct route.
Because of the hyperbolic geometry of Minkowski space, a scenic route will always rack up more distance and less time than a direct route.
This is a property of the routes, and a property of the geometry of spacetime! It is not a property of the clocks or odometers.
I repeat: It is the ordinary Muggle experience that the elapsed time from A to D is independent of path ... but this is not the right answer in general! In general, elapsed time is path-dependent. Get used to it. All the “proofs” that Moe’s clock runs slow are based on the implicit assumption that time “should” be path-independent. However, there is another interpretation that is far simpler and far more consistent with the structure of the Lorentz group, namely that the clocks are not broken or distorted, and that the notion of elapsed time is path-dependent, just as path-length is path-dependent.
I don’t think it is helpful to argue that things “are” as they appear to be, or that things “are” whatever we measure them to be. Appearances can be deceiving, and some measurements are incomplete and/or non-intrinsic. See reference 7 for some background on this point. A ruler subtends a certain angle in my field of view. I can measure this angle, but it may not tell me anything about the proper length of the ruler, if I don’t account for other factors such as orientation.
A ruler is a ruler. Its length is its proper length. A clock is a clock. Its time is its proper time. The projection of a ruler onto the wall of the cave is not a ruler; it is just a projection.
Thanks to David Bowman for pointing out the analogy between the twins puzzle and an ordinary merry-go-round.