THE JOUKOWSKI TRANSFORMATION

We introduce the conformal transformation due to Joukowski (who is pictured above)

displaymath42

and analyze how a cylinder of radius R defined in the z plane maps into the z' plane:

  1. If the circle is centered at (0, 0) and tex2html_wrap_inline50 the circle maps into the segment between tex2html_wrap_inline54 and tex2html_wrap_inline56 lying on the x-axis;
  2. If the circle is centered at tex2html_wrap_inline58 and tex2html_wrap_inline60, the circle maps in an airfoil that is symmetric with respect to the x'-axis;
  3. If the circle is centered at tex2html_wrap_inline64 and tex2html_wrap_inline66, the circle maps into a curved segment;
  4. If the circle is centered at tex2html_wrap_inline68 and tex2html_wrap_inline70, the circle maps into an asymmetric airfoil.

To summarize, moving the center of the circle along the x-axis gives thickness to the airfoil, moving the center of the circle along the y-axis gives camber to the airfoil.

In the following interactive application it is possible to move the center of the circle in the z plane and see the resulting transformed airfoil.

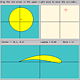We need to introduce some notations on airfoils.

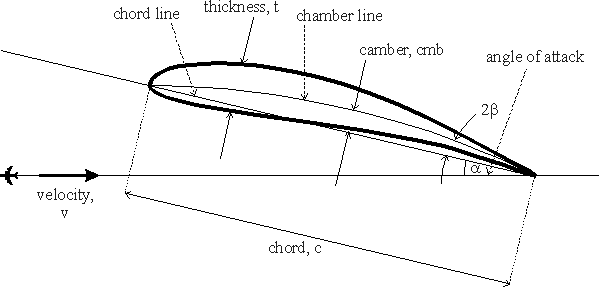
The generic Joukowski airfoil has a rounded leading edge and a cusp at the trailing edge where the camber line forms an angle tex2html_wrap_inline87 with the chord line. In the cylinder plane, tex2html_wrap_inline89 is related to the vertical coordinate of the center of the cylinder so that

displaymath49

Usually the angle of attack (sometimes called physical) is defined as the angle tex2html_wrap_inline95 that the uniform flow forms with the chord line. More interesting for aerodynamics is the angle

displaymath51

In fact, when the angle tex2html_wrap_inline97 is zero, the lift, as will be shown, vanishes. Then the angle tex2html_wrap_inline97 is often defined as the effective angle of attack.

INDEX