|
| |
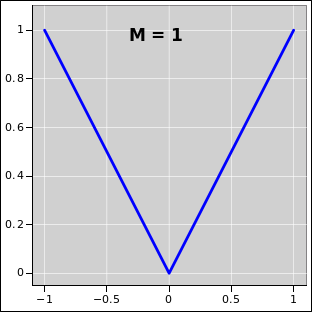
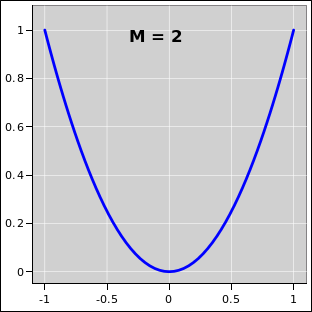
| Figure 25.1: M = 1 i.e. Linear Power-Law Potential Well | Figure 25.2: M = 2 i.e. Quadratic Power-Law Potential Well | |
In this chapter we temporarily lower our standards and derive some results that apply only in the classical limit, specifically in the “energy continuum” limit. That is, we assume that the temperature is high compared to the spacing between energy levels, so that when evaluating the partition function we can approximate the sum by an integral. We further assume that the system occupies a bounded region in phase space. That is, we assume there is zero probability that any of the position variables or momentum variables will ever take on super-large values.
Subject to these provisos, we1 can write the partition function as:
| (25.1) |
Here we intend x and v to represent, somewhat abstractly, whatever variables contribute to the energy. (We imagine that x represents the variable or variables that contribute to the potential energy, while v represents the variable or variables that contribute to the kinetic energy, but this distinction is not important.)
Using 20/20 hindsight, we anticipate that it will be interesting to evaluate the expectation value of ∂E/∂ln(x) | v. We can evaluate this in the usual way, in terms of the partition function:
| (25.2) |
We now integrate by parts. The boundary terms vanish, because we have assumed the system occupies a bounded region in phase space.
| (25.3) |
We can of course write a corresponding result for the v-dependence at constant x:
| (25.4) |
and if there are multiple variables {xi} and {vi} we can write a corresponding result for each of them. This is called the generalized equipartition theorem.
An interesting corollary is obtained in the case where the energy contains a power-law term of the form Ej = |x|M:
| (25.5) |
In the very common case where M=2, this reduces to
| (25.6) |
and if the total energy consists of a sum of D such terms, the total energy is
| (25.7) |
This result is the quadratic corollary to the equipartition theorem. The symbol D▯ (pronounced “D quad”) is the number of quadratic degrees of freedom of the system. Here we are assuming every degree of freedom appears in the Hamiltonian either quadratically or not at all.
All too often, equation 25.7 is called simply “the” equipartition theorem. However, we should beware that it it is only a pedestrian corollary. It only applies when every degree of freedom contributes to the energy either quadratically or not at all. This includes a remarkably large number of situations, including the harmonic oscillator, the particle in a box, and the rigid rotor ... but certainly not all situations, as discussed in section 25.3.
Also keep in mind that all the results in this chapter are based on the assumption that the system is classical, so that in the definition of the partition function we can approximate the sum by an integral.
Let us consider a particle moving in one dimension in a power-law potential well. The energy is therefore
| (25.8) |
where the first term represents the usual kinetic energy (in some units) and the second term represents the potential energy. The case M=2 corresponds to a harmonic oscillator, as shown in figure 25.2.
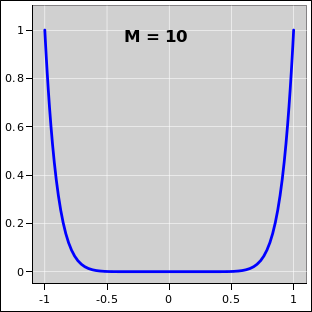
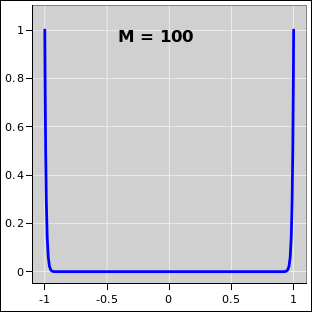
As M becomes larger and larger, the situation begins to more and more closely resemble a square-well potential, i.e. a particle in a box, as you can see in figure 25.3 and figure 25.4.

|

| |
| Figure 25.1: M = 1 i.e. Linear Power-Law Potential Well | Figure 25.2: M = 2 i.e. Quadratic Power-Law Potential Well | |
|
| |
| Figure 25.3: M = 10 Power-Law Potential Well | Figure 25.4: M = 100 Power-Law Potential Well | |
Let us apply the generalized equipartition theorem, namely equation 25.3 and equation 25.4, to each of these situations.
| (25.9) |
It must be emphasized that every degree of freedom counts as a degree of freedom, whether or not it contributes to the heat capacity. For example, consider a free particle in three dimensions:
| There are six degrees of freedom. | There are only three quadratic degrees of freedom. |
| All six of the degrees of freedom contribute to the entropy. This should be obvious from the fact that the phase space of such a particle is six dimensional. | Only three of the degrees of freedom contribute to the heat capacity. |