1 How Names Should Be Used, or Not

A titmouse is not a mouse. Buckwheat is not wheat. As Voltaire pointed out, the Holy Roman Empire was in no way holy, nor Roman, nor an empire. Additional examples of weird terminology can be found in section ‍2.

It is important to keep in mind the simple rule:

Most names should be considered idiomatic expressions. As such, they should not be taken literally.

Names exist for a reason. Many of the things we deal with on a daily basis are not easy to describe in detail; it would take several sentences or even several pages for a full description. A fully-descriptive name would be far too long to be useful. Therefore we have dictionaries, encyclopedias, glossaries, and cartographic legends. We can look up a name or symbol to find out what it means.

It must be emphasized that ideas are primary and fundamental, while terminology is tertiary. Terminology is important only insofar as it helps us think about and talk about the ideas.

We get into trouble when the name is ambiguous (the same name applied to multiple distinct ideas) ... or when the name appears to be descriptive but is misleading.

• When confronted with misleading terminology, sometimes it suffices to lift the ambiguity by using adjectives. For instance, if we mean adiabatic in the sense of thermally isolated, we can always say “thermally isolated” — and if we mean adiabatic in the sense of non-sudden, we can always describe something as “non-sudden” or “gradual” or “preserving corresponding states”.
• Sometimes it is necessary to coin new terminology. For example, consider the contrast:

  “Inaction” is the opposite of “action”, just as “inaudible” is the opposite of “audible”. As a rule, in English, the prefix “in–” negates the meaning of the word that follows. Many, many words follow this rule.

  “Inflammable” means the same thing as “flammable”. The prefix “in–” does not negate “flammable”, so this is an exception to the usual rule. If you follow the rule, you will get the meaning diametrically wrong.

  The word “invaluable” does not negate the root word, and indeed intensifies it.

  It has long been known that the word “inflammable” is misleading to a dramatically dangerous degree. Therefore there was a concerted effort get rid of that word entirely, and to standardize on “flammable”. However, related words such as “inflammatory” are still extremely common.

• When confronted with terminology that is merely non-descriptive (but not ambiguous or unduly misleading), trying to improve the terminology is usually not worth the trouble. A name is not a description, and never will be.
• As another way of expressing the same idea: Never judge a book by its cover.

1.1 Birdwatching with the Feynmans

Richard Feynman was fond of pointing out that knowing the name of a thing is not equivalent to understanding a thing. In reference ‍1 he wrote:

The next day, Monday, we were playing in the fields and this boy said to me, “See that bird standing on the stump there? What’s the name of it?”

I said, “I haven’t got the slightest idea.”

He said, “It’s a brown-throated thrush. Your father doesn’t teach you much about science.”

I smiled to myself, because my father had already taught me that [the name] doesn’t tell me anything about the bird. He taught me “See that bird? It’s a brown-throated thrush, but in Germany it’s called a halsenflugel, and in Chinese they call it a chung ling and even if you know all those names for it, you still know nothing about the bird – you only know something about people; what they call that bird. Now that thrush sings, and teaches its young to fly, and flies so many miles away during the summer across the country, and nobody knows how it finds its way,” and so forth. There is a difference between the name of the thing and what goes on.

The result of this is that I cannot remember anybody’s name, and when people discuss physics with me they often are exasperated when they say “the Fitz-Cronin effect,” and I ask “What is the effect?” and I can’t remember the name.

In my opinion, the young Feynman made a mistake by over-reacting. Knowing the name of the bird does in fact tell you something. First of all, there is a good chance that a brown-throated thrush is related to other thrushes, and that tells you quite a lot, if you have studied other thrushes. And even if this is the first thrush you’ve ever seen, or even the first bird, knowing that it is a brown-throated thrush allows you to look it up in reference books, and thereby find out enormous amounts of information.

Names are a tool. As such, they can be used wisely or unwisely:

1.2 Choosing Names

In general, you should not expect names to be descriptive ... and even if you have a chance to give something a descriptive name, please do not to overboard in that direction. For example, when naming the variables and the subroutines in a computer program, oftentimes it would take several sentences or several paragraphs to fully describe what the thing does, which is too long for a convenient name. It is better to give it a short name and then write into the documentation a legend that says what the name means. For more on this, see reference ‍2.

1.3 Multi-Word Phrases

Oftentimes, the meaning of a noun or verb is heavily modified by the surrounding words, even if the core meaning remains more-or-less the same. For example, consider

• dollar bill,
• electricity bill,
• senate bill,
• et cetera

Here’s a more complex example. Consider the constrast:

Note that in example (a) we have 3 groups of 7, while in example (b) we have 7 groups of 3. Meanwhile, in examples (a) and (b) we have X/Y=7, while in example (c) the fraction is upside down: Y/X=7.

Overall, inconsistent terminology gives rise to multiple problems:

• A minor problem is that if somebody asks you what a given word means, it is impossible to give a concise answer. It all depends on how the word is used.
• A much more serious problem is that if you know what a word means in one context, you might assume it has the same meaning in another context. This can lead to serious mistakes. It’s easy to have high confidence in the wrong answer, which makes things even worse.

If you’re lucky, the intended meaning can be figured out by sufficiently close reading of the sentence; the examples in this section are in this category. However, things can get much worse than that: Sometimes the meaning depends on the broader context, and sometimes it’s just hopelessly ambiguous.

2 Some Examples

The following list gives some examples where the name of the thing provides a conspicuously poor description of the thing ... or where the same word has multiple wildly-divergent meanings.

It should go without saying that this list is nowhere near complete. These few examples should suffice to make the point that names are not the same as descriptions, and you should not read too much into a name.

1. ‍ ‍ ‍ As mentioned in section ‍1, a titmouse is not a mouse. It’s a bird.

Figure ‍1: Tufted Titmouse

2. ‍ ‍ ‍ As mentioned in section ‍1, buckwheat is not a kind of wheat. Taxonomically, both wheat and buckwheat are in the plant kingdom, but that’s as close as the relationship gets.

3. ‍ ‍ ‍ As mentioned in section ‍1, the Holy Roman Empire was in no way holy, nor Roman, nor an empire. See reference ‍3.

4. ‍ ‍ ‍ A peacock mantis shrimp is neither a peacock nor a mantis. Also not a shrimp; they’re both soft-shell crustaceans, but that’s as close as it gets.

Figure ‍2: Peacock Mantis Shrimp

5. ‍ ‍ ‍ The Nazis called themselves the National Socialist Workers’ Party, but they weren’t socialists. They hated socialists and socialism; see reference ‍4 and reference ‍5.

6. ‍ ‍ ‍ Even something as crucial and fundamental as the word “and” has conflicting meanings:

In ordinary English, if somebody says A and B and C and D are on top of the table, as we increase the number of terms in the and-expression, the set of objects gets larger.

In Boolean algebra and formal logic, the and operator denotes the intersection of sets. If somebody speaks of A and B and C and D, as we increase the number of factors in the and-expression, the number of objects gets smaller (or stays the same).

7. ‍ ‍ ‍ The equal sign is also crucial and fundamental, yet the meaning is context-dependent:

In mathematics, A = B means exactly the same thing as B = A. It’s completely symmetrical, by definition.

In many computer languages such as C++, fortran, or basic, the assignment statement A = B means something wildly different from B = A. There’s nothing symmetrical about it.

There are some rather serious misconceptions about this, having to do with equivalence versus causation, in connection with the laws of physics, as discussed in reference ‍6.

The Algol computer language uses the “:=” symbol for assignment statements, which has an appropriately asymmetrical appearance. Meanwhile, the Macsyma language (like its clone, Maxima) uses the “:=” symbol for defining functions. Oddly enough, it uses a simple “:” for assignment statements. This symbol has a less-than-ideal symmetrical shape, but at least it does not directly conflict with the mathematical “=” sign.

8. ‍ ‍ ‍

Sometimes the term “in general” refers to something that is generally true, i.e. typically true, but not always true.

Sometimes the term “in general” refers to something that is true in all generality, i.e. absolutely, universally true.

Because of the ambiguity, I prefer to avoid the term (except in negative constructions). Alternatives include saying “as a decent rule of thumb” (if that’s what I mean) or saying “in all generality” (if that’s what I mean). Very few things are true in all generality; even the most basic theorems are subject to important provisos, restrictions, and assumptions.

9. ‍ ‍ ‍ A first-quarter moon is halfway to being a full moon.

10. ‍ ‍ ‍

A north wind (aka northerly wind) blows from the north. Similarly, when you are at the beach, a sea breeze blows from the sea, and a land breeze blows from the land.

An offshore breeze blows toward the offshore area, and similarly an onshore breeze blows toward the onshore area.

11. ‍ ‍ ‍

The arrowhead on a barnyard weathervane points into the wind, i.e. pointing to the direction the wind is blowing from. The fletching and most of the shaft get blown to the downwind side.

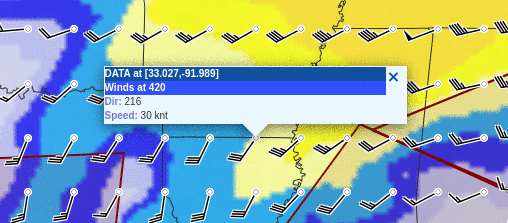
The wind indicators on a NOAA weather charts are drawn from the station into the wind. The shaft is on the upwind side, very unlike a weather vane. The barbs on the symbol resemble fletching on an arrow. The arrow points downwind toward the station, again very unlike a weathervane. See figure ‍3 and figure ‍4. Where it says “Winds at 420” (white on a blue background) that refers to Flight Level 420, ı.e. 42,000 feet MSL.

Figure ‍3: Surface Observations : Barb Into the Wind

Figure ‍4: Winds Aloft : Barb Into the Wind

If you don’t think this is odd, try teaching it to a bunch of students who think it’s simple and think they already understand it. See reference ‍7.

12. ‍ ‍ ‍ Asparagus fern is not a fern. Taxonomically, actual ferns and asparagus ferns are both in the plant kingdom, but that’s as close as the relationship gets.

13. ‍ ‍ ‍ A naked mole rat is neither a mole nor a rat. Rats and naked mole rats are rodents, but moles are not.

14. ‍ ‍ ‍ A fisher cat is not in the cat family (felidae), and has never been observed to catch or eat fish.

15. ‍ ‍ ‍ The Jerusalem artichoke is not an artichoke and doesn’t come from Jerusalem.

16. ‍ ‍ ‍

As mentioned in section ‍1, the prefix “in−” is widely used to form opposites. For example, “inaction” is the opposite of “action”, and “invertebrate” is the opposite of “vertebrate”.

The word “inflammable” means the same thing as “flammable”. This does not conform to the usual pattern. It is remarkably and dangerously misleading.

17. ‍ ‍ ‍

In swimming, one lap is one length of the pool. It takes two laps to get back to the starting place.

On a running track, one lap is once around the track, back to the starting place.

18. ‍ ‍ ‍

The races were sanctioned by the state council. (Meaning approved.)

Two of the runners were sanctioned by the state council. (Meaning disapproved and penalized.)

This is a contranym.

19. ‍ ‍ ‍

We speak of the “alkali metals” as being disjoint from the “alkali earths”.

The alkali earths are perfectly good metals.

20. ‍ ‍ ‍ Given that “acid” is pretty much the opposite of “alkali”, you might imagine that “acidity” would be the opposite of “alkalinity”, but it’s not. The alkalinity of a weak base is proportional to concentration, but the acidity of a weak acid is not (assuming the concentration is not too low).

Constructive suggestion: It helps to avoid the term “acidity” as much as possible. If you mean low pH, say low pH.

The whole notion of “alkalinity” (aka “total alkalinity”) always struck me as unsophisticated and underspecified. Buffer behavior is complicated, not easily characterized by a single number. Sometimes you care about the local height, and sometimes you care about the area under the curve.

21. ‍ ‍ ‍

Astronomers use the name “metals” to apply to any elements other than hydrogen and helium.

Chemists, metallurgists, and ordinary folks share a notion of “metal” that is very much narrower than the astronomers’ notion.

22. ‍ ‍ ‍

In the context of an electrical harmonic oscillator, such as one standing-wave mode of the electromagnetic field, we say that the Nth energy eigenstate has N “photons” in it. The operator a†a is the photon-number operator. These photons do not propagate at the speed of light; indeed they do not propagate at all. They are standing waves ... or in the case of the simple harmonic oscillator, not really waves at all.

In the context of a propagating wave, a “photon” is a wavepacket, typically a Gaussian wavepacket, with some not-too-large spread in position and also some not-too-large spread in momentum.

23. ‍ ‍ ‍ A photomultiplier tube does not multiply photons. It basically consists of a wimpy little photo-electron emitter, followed by an N-stage electron multiplier. You can think of it as a photo-electron-multiplier. (The same sort of electron multiplier is used in mass spectrometers, where the first-stage input is an ion, rather than a photo-electron.)

24. ‍ ‍ ‍

The so-called “first ionization energy” should really be called the “first cationization energy”. It applies when you are removing an electron.

If you are making an anion, i.e. adding an electron, you should use the “electron affinity” instead.

25. ‍ ‍ ‍

We speak of “oxygen” (from the Greek, meaning literally “acid former’) and “halogens” (literally “salt formers”).

For every salt there is a corresponding acid, and for every acid there is a corresponding series of salts. So how can oxygen and halogen be disjoint notions? Every acid-former should also be a salt-former, and vice versa.

26. ‍ ‍ ‍

We speak of the “rare earths”.

They are not particularly rare. For example, cerium is slightly more abundant than copper.

27. ‍ ‍ ‍

The noun “day” can refer to the hours of daylight (roughly a 12-hour day).

It can also refer to the complete 24-hour cycle.

Ditto for the adjectives “daily” and “diurnal”. As far as I can tell the ambiguity has existed for centuries, dating back to the Latin dies and diurnus.

28. ‍ ‍ ‍

Bimonthly “usually” means once every two months.

According to the American Heritage Dictionary, it can also mean twice per month. On the other hand, other dictionaries label the latter definition as rare or erroneous.

This is a contranym. The same ambiguity arises for other words such as biweekly.

29. ‍ ‍ ‍

In one of its meanings, ravel is the opposite of unravel.

In another of its meanings, ravel is exactly the same as unravel.

This is a contranym.

30. ‍ ‍ ‍

We speak of cooking things “in the microwave”.

That refers to a microwave oven, which is an oven, not a microwave (nor, indeed, a wave of any kind).

The microwaves in such an oven have a wavelength that is not microscopic, is not micron-sized, and is in fact much longer than the wavelength of the waves that do the cooking in a plain old broiler.

31. ‍ ‍ ‍

Sometimes “X-ray” refers to a particular part of the electromagnetic spectrum.

Sometimes “X-ray” refers to an image made using this part of the spectrum.

32. ‍ ‍ ‍

I recently cooked some “French fries”. I cooked them in the oven, in accordance with instructions on the package.

That resulted in “French fries” that had never been fried and had never been anywhere near France.

33. ‍ ‍ ‍

I recently bought some Mexican oregano (Lippia graveolens).

It wasn’t oregano (Origanum vulgare) and it had never been in Mexico.

34. ‍ ‍ ‍

Wish-Bone sells something called “French dressing”.

It doesn’t come from France, and does not resemble anything commonly served in France.

35. ‍ ‍ ‍ The meaning of the word “organic” is heavily dependent on context:

1. “Organic chemistry” is a two-word idiomatic expression.
2. “Organic vegetables” is a two-word idiomatic expression.
3. “Organic disease” is a two-word idiomatic expression.
4. “Pipe organ” is a two-word idiomatic expression.

None of these four meanings have much in common nowadays. They are all rather distantly related to the original root, namely instrument or mechanism.

Neither the chemists nor the physicians should be telling the farmers how to define farming-related terms ... and vice versa, in all combinations.

36. ‍ ‍ ‍ In chemistry, the technical definition of “aromatic” is highly technical, idiomatic, and far removed from the ordinary nontechnical meaning.

37. ‍ ‍ ‍

In mechanics, we speak of “kinetic energy” as being disjoint from “potential energy”.

In thermodynamics, we speak of the “chemical potential”. A large part of the chemical potential consists of kinetic energy.

38. ‍ ‍ ‍

In physics, conservation of momentum means that the amount of momentum in a region cannot change except insofar as it flows across the boundary. See equation ‍1. Energy, momentum, and electrical charge are always strictly conserved.

In a non-technical context, conservation means something very different, namely avoiding waste. For example: conservation of endangered wildlife.

39. ‍ ‍ ‍

In physics, the notion of energy is fundamental and very important. It is a state function, i.e. a function of the state of a give system or parcel.

The homespun term “energy” refers to something else. It is not the physics energy, or even the thermodynamic free energy. Roughly speaking, it is the amount of thermodynamically available energy. It is not a function of state, since it depends on the parcel’s surroundings.

Along with item 38, this shows that in the expression “conservation of energy”, both the word conservation and the word energy have dramatically different meanings, depending on whether you are speaking in physics terms or homespun terms.

40. ‍ ‍ ‍

We speak of the “free energy”.

Although it has dimensions of energy, it is not the actual energy.

Also, it’s not free, since you usually have to pay for it.

41. ‍ ‍ ‍

By itself, the word radio brings to mind electromagnetism in the kHz to MHz part of the spectrum, where the energy is 5×10−11 to 5×10−7 eV per photon.

The term radioactivity, which comes from the same root, brings to mind photons and particles with energy above 105 eV per particle.

So radioactivity is separated from radio by 12 orders of magnitude.

42. ‍ ‍ ‍

The term “bedlam” refers to uproar and confusion.

The word is derived from “Bethlehem”, which carries no such meaning.

43. ‍ ‍ ‍

In molecular spectroscopy we speak of “internal conversion”.

The conversion is not usually internal to the molecule.

44. ‍ ‍ ‍

Originally, “elastic” meant capable of returning to its original size and shape after being stretched. This meaning is still common in technical meanings such as the elastic limit of a spring, and in many nontechnical meanings such as an elastic band in clothing. In this sense, rubber is far more elastic than steel.

In physics there is another, much narrower meaning: we speak of an inelastic collision between two soft rubber balls, even if the two balls return to their original shape. In this sense, steel has a far greater coefficient of elasticity than rubber.

45. ‍ ‍ ‍

In the printing trades, and in the physics lab, the colors red, green, and blue are very different from the colors cyan, magenta, and yellow.

In, say, a clothing store, cyan is considered a shade of blue. If you want a cyan-colored shirt, you should ask for blue (or bright blue); if you ask for cyan the clerk probably won’t understand you. If you want a technically blue-colored shirt, you might ask for deep blue.

46. ‍ ‍ ‍

The SI “mole” is defined as the base unit for “amount of substance”. This is a subtle, highly abstract notion. It is much older than atomic theory, and does not depend counting particles of any kind.

Nowadays a lot of people define “mole” in terms of Avogadro’s number. A mole is a number, like a dozen (only larger).

For all practical purposes, a mole is equal to the number of 12C atoms (or the “amount of substance”) in twelve grams of 12C. However, twelve kilograms would have made SI more consistent. One occasionally sees definitions of the terms gram-mole and kilogram-mole, but these are not SI terms and are vanishingly rare in practice.

47. ‍ ‍ ‍

In some situations, adiabatic means fast enough ... so that there are no appreciable heat leaks through the boundary.

In some situations, adiabatic means slow enough or gentle enough ... so that there is a one-to-one correspondence between initial states and final states, with no change in occupation numbers. This is the opposite of the “sudden” approximation. See reference ‍9.

48. ‍ ‍ ‍

In thermodynamics, experts use at least four or five mutually-inconsistent reasonable technical definitions of “heat”, each of which has its advantages and disadvantages. See reference ‍10.

Four or five different reasonable technical definitions is bad enough, but there are also innumerable less-reasonable, non-technical, and/or metaphorical uses of the word.

49. ‍ ‍ ‍

Rock candy is not made of rock.

Rock wool is not made of wool.

Milk of magnesia is not made of milk.

Chocolate turtles are not made of turtles.

This goes to show that the English language’s rules for forming appositives are rather loose.

50. ‍ ‍ ‍

In the terms “frequency spectrum” and “mass spectrometer”, frequency and mass (respectively) are the abscissa of the spectrum.

In the terms “power spectrum” and “emission spectrum”, power and emission (respectively) are the ordinate of the spectrum.

51. ‍ ‍ ‍

Sometimes “spin zero” means s=0, which is related to the eigenvalue of the S2 operator.

Sometimes “spin zero” means ms=0, which is the eigenvalue of the Sz operator.

It is not hard to construct sentences which use the word “spin” with two different meanings in the same sentence. It is not hard to get thoughtful experts to accept such sentences at face value, even after being warned that a trick question is coming.

52. ‍ ‍ ‍

We speak of electrons “flowing” in a wire. Also, since electrons carry charge, we speak of charge “flowing” in a wire. Charge density appears on the LHS of equation ‍1. “Flow” means that charge is being carried from place to place.

We speak of current “flowing” in a wire. Current density appears on the RHS of equation ‍1. “Flow” does not mean that current is being carried from place to place.

The equation for continuity of flow is: ∂ρ ∂t  = − ∇·j  ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍(1)

53. ‍ ‍ ‍ Although the ambiguity of “flow” as mentioned in item 52 isn’t very troublesome when restricted to the “flow” of charge or the “flow” of current, it becomes much more serious when we talk about the “flow” of momentum. A vortex in a fluid is a pattern of flow, wherein the fluid flows around and around. But what do we say if the vortex itself is being carried from place to place? Is that the flow of flow? See also reference ‍11.

54. ‍ ‍ ‍

When drawing the vector that represents an electric dipole moment, physicists, mathematicians, and some (but not all!) chemists draw it in a way that is consistent with the orientation of position vectors.

Some chemistry books (especially at the introductory level) draw the arrow the other way. This makes no sense, but they do it anyway. See reference ‍12 for details.

55. ‍ ‍ ‍

Suppose we have two parallel plates, with a charge Q/2 on each of them. We say there is a charge Q on the pair of plates, referring to the actual total charge.

Suppose we have a parallel-plate capacitor, with a charge +Q on one plate and a charge −Q on the other plate. It is conventional (but unwise) to say there is a “charge” Q on the capacitor.

There are innumerable intermediate cases.

I strongly recommend reserving the term “charge” for the real total charge.

Constructive suggestion: We can use the term gorge to represent the capacitor situation. We can speak of gorging and disgorging the capacitor. See reference ‍13.

56. ‍ ‍ ‍ In mathematics, the term “linear” has multiple inconsistent meanings.

The term “linear equation” covers things like y = m x + b.

The term “linear transformation” covers the mapping from x to m x but does not include the mapping from x to m x + b (unless by some miracle b is identically zero).

To avoid the inconsistency, the easiest thing is to avoid the term “linear” entirely. You can refer to y = m x + b as an affine relationship and refer to y = m x as a proportionality relationship.

57. ‍ ‍ ‍ True north ... versus magnetic north ... versus polar grid north.

58. ‍ ‍ ‍ Consider the following pattern:

sin4(x)  ‍ =  ‍ [ sin(x) ]4  ‍ ‍ ‍ ‍ as expected   sin3(x)  ‍ =  ‍ [ sin(x) ]3  ‍ ‍ ‍ ‍ as expected   sin2(x)  ‍ =  ‍ [ sin(x) ]2  ‍ ‍ ‍ ‍ as expected   sin−1(x)  ‍ =  ‍ arcsin(x)  ‍ ‍ ‍ ‍ surprise!      ‍ ≠  ‍ [ sin(x) ]−1  ‍ ‍ ‍ ‍ surprise!

‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍ ‍(2)

In other words, you might expect sin⁻¹(x) to be the multiplicative inverse of sin(x), but instead it is more-or-less universally interpreted to mean the functional inverse, i.e. the inverse function.

Similar words apply to other trigonometric functions (cosine, tangent, cotangent, et cetera).

59. ‍ ‍ ‍ The “Dirac delta function” is not a function, according to the mathematical definition of function. It could more properly be called a delta distribution, but almost nobody calls it that.

60. ‍ ‍ ‍

When a switch is closed, electrical current can flow.

When a valve is closed, no fluid can flow.

61. ‍ ‍ ‍ In classical mechanics, a closed system cannot exchange matter or energy with its surroundings; in thermodynamics this would be called an isolated system. In thermodynamics, especially as practiced by chemists, a closed system is closed with respect to matter but can still exchange energy with its surroundings.

62. ‍ ‍ ‍ In mathematics, even just within topology, there are multiple definitions of “closed”.

• In topology, a manifold is “closed” if it is compact and without boundary.
• In point-set topology, a set is “closed” if it contains all its limit points.
• In differential topology, a one-form is “closed” if its exterior derivative vanishes everywhere.

63. ‍ ‍ ‍

In mathematics, the term “field” could refer to a vector field.

Or it could refer to a Galois field.

64. ‍ ‍ ‍ The word “algebra” has many inconsistent meanings.

• High-school algebra – a field of study
• Abstract algebra (groups, rings, etc.) – a field of study
• Algebra i.e. a vector space with multiplication – a mathematical structure
• Boolean algebra – another structure
• Sigma algebra – yet another structure

For more examples, see reference ‍14. It’s hard to see what these different algebras have in common. In particular, it’s hard to predict what sorts of mathematical structures will be called algebras and which won’t.

Even in the context of high-school algebra, the word has two different meanings: Fundamentally, algebra is a language for expressing rules, patterns, and generalizations. However, when most people hear the word “algebra” they think of solving equations to find x.

65. ‍ ‍ ‍

In mathematics, an element y of a group is called “primitive” if every element of the group is equal to some power of y. For example, in the group of integers mod 7, the element 3 is primitive, while the element 2 is not.

Let F be the field of polynomials over some base field G. An element P of F is called “primitive” if every element of the field (F mod P) is equal to some power of the monomial x. For example, x2+x+1 is primitive in the field of polynomials over GF[2], but it is not primitive in the field of polynomials over GF[5].

This is demonstrably a source of real (not hypothetical) confusion. A well-known cryptography book quoted one definition of “primitive” in a context where the other definition was required.

66. ‍ ‍ ‍

The term “generator” is also ambiguous. According to one definition, the element y in item 65 is called a “generator” of the group.

Let F be the field of polynomials over some base field G. Let P be an irreducible element of F. Then P is called the “generator” of the field (F mod P).

(IMHO it would be good to do away with this usage, and instead call P the modulus.)

67. ‍ ‍ ‍

“Event” in spacetime, in physics.

“Event” in statistics.

68. ‍ ‍ ‍

“Sample” in chemistry.

“Sample” in statistics. See reference ‍15.

69. ‍ ‍ ‍

“Gravity” in the sense of framative gravity.

“Gravity” in the sense of massogenic gravity. See reference ‍16.

70. ‍ ‍ ‍

“Acceleration” (the vector).

“Acceleration” (the scalar). See reference ‍17.

71. ‍ ‍ ‍

Textbooks commonly define «power» as the rate of doing mechanical work.

In practice, «power» is used much more broadly. I get almost twice as many hits from googling “watts of thermal power” than from “watts of mechanical power”.

Some argue that any transfer or transformation of energy should count as «power» ... but I’m not sure advection should count. For example, consider a slow leak in the gas tank of a car. Does that count as «power»? I’ve pretty much given up. I consider this one of the supposedly technical terms that doesn’t have any clear meaning. Anybody who wants to use it should explicitly specify the intended meaning.

3 References

1.

Richard Feynman,
“What is Science”
(an address to the National Science Teachers Association)
The Physics Teacher 7, 6, 313–320 (1968).
http://www.fotuva.org/feynman/what_is_science.html

2.

John Denker,
“Suggestions for Writing Good Software”
www.av8n.com/computer/htm/good-software.htm

3.

Voltaire, Essai sur l’histoire générale et sur les mœurs et l’esprit des nations, Chapter 70 (1756).

4.

David Emery, “Were the Nazis Socialists?”
https://www.snopes.com/news/2017/09/05/were-nazis-socialists/

5.

Ronald J. Granieri, “The right needs to stop falsely claiming that the Nazis were socialists”
https://www.washingtonpost.com/outlook/2020/02/05/right-needs-stop-falsely-claiming-that-nazis-were-socialists/

6.

John Denker,
“Cause and Effect”
www.av8n.com/physics/causation.htm

7.

https://www.aviationweather.gov/windtemp

8.

Wiktionary has a list containing more than a hundred contranyms:
https://en.wiktionary.org/wiki/Category:English_contranyms

9.

John Denker,
“Modern Thermodynamics”
./thermo/

10.

ibid., the chapter on “Heat”
./thermo/heat.html

11.

John Denker,
“A Non-Sneaky Derivation of Euler’s Equation”
www.av8n.com/physics/euler-flow.htm

12.

John Denker,
“The Electric Dipole Moment Vector – Direction, Magnitude, Meaning, et cetera”
www.av8n.com/physics/electric-dipole.htm

13.

John Denker,
“Gorge versus Charge”
www.av8n.com/physics/gorge-vs-charge.htm

14.

Wikipedia article, “Algebra (disambiguation)”
http://en.wikipedia.org/wiki/Algebra_(disambiguation)

15.

John Denker,
“Introduction to Probability”
www.av8n.com/physics/probability-intro.htm

16.

John Denker,
“Weight, Gravitational Force, Gravity, g, Latitude, et cetera”
www.av8n.com/physics/weight.htm

17.

John Denker,
“Velocity, Speed, Acceleration, and Deceleration”
www.av8n.com/physics/acceleration.htm