Figure 0.1: Thermodynamics, Based on Energy and Entropy
Real thermodynamics is celebrated for its precision, power, generality, and elegance. However, all too often, students are taught some sort of pseudo-thermodynamics that is infamously confusing, lame, restricted, and ugly. This document is an attempt to do better, i.e. to present the main ideas in a clean, simple, modern way.
| The first law of thermodynamics is usually stated in a very unwise form. | We will see how to remedy this. |
| The second law is usually stated in a very unwise form. | We will see how to remedy this, too. |
| The so-called third law is a complete loser. It is beyond repair. | We will see that we can live without it just fine. |
| Many of the basic concepts and terminology (including heat, work, adiabatic, etc.) are usually given multiple mutually-inconsistent definitions. | We will see how to avoid the inconsistencies. |
Many people remember the conventional “laws” of thermodynamics by reference to the following joke:1
It is not optimal to formulate thermodynamics in terms of a short list of enumerated laws, but if you insist on having such a list, here it is, modernized and clarified as much as possible. The laws appear in the left column, and some comments appear in the right column:
| The zeroth law of thermodynamics tries to tell us that certain thermodynamical notions such as “temperature”, “equilibrium”, and “macroscopic state” make sense. | Sometimes these make sense, to a useful approximation … but not always. See chapter 3. |
| The first law of thermodynamics states that energy obeys a local conservation law. | This is true and important. See section 1.2. |
| The second law of thermodynamics states that entropy obeys a local law of paraconservation. | This is true and important. See chapter 2. |
| There is no third law of thermodynamics. | The conventional so-called third law alleges that the entropy of some things goes to zero as temperature goes to zero. This is never true, except perhaps in a few extraordinary, carefully-engineered situations. It is never important. See chapter 4. |
To summarize the situation, we have two laws (#1 and #2) that are very powerful, reliable, and important (but often misstated and/or conflated with other notions) plus a grab-bag of many lesser laws that may or may not be important and indeed are not always true (although sometimes you can make them true by suitable engineering). What’s worse, there are many essential ideas that are not even hinted at in the aforementioned list, as discussed in chapter 5.
We will not confine our discussion to some small number of axiomatic “laws”. We will carefully formulate a first law and a second law, but will leave numerous other ideas un-numbered. The rationale for this is discussed in section 7.10.
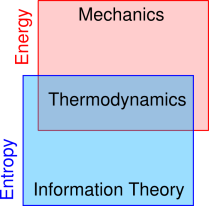
The relationship of thermodynamics to other fields is indicated in figure 0.1. Mechanics and many other fields use the concept of energy, sometimes without worrying very much about entropy. Meanwhile, information theory and many other fields use the concept of entropy, sometimes without worrying very much about energy; for more on this see chapter 22. The hallmark of thermodynamics is that it uses both energy and entropy.
This section is meant to provide an overview. It mentions the main ideas, leaving the explanations and the details for later. If you want to go directly to the actual explanations, feel free to skip this section.
Most of the fallacies you see in thermo books are pernicious precisely because they are not absurd. They work OK some of the time, especially in simple “textbook” situations … but alas they do not work in general.
The main goal here is to formulate the subject in a way that is less restricted and less deceptive. This makes it vastly more reliable in real-world situations, and forms a foundation for further learning.
In some cases, key ideas can be reformulated so that they work just as well – and just as easily – in simple situations, while working vastly better in more-general situations. In the few remaining cases, we must be content with less-than-general results, but we will make them less deceptive by clarifying their limits of validity.
| On the left side of the diagram, the system is constrained to move along the red path, so that there is only one way to get from A to Z. | In contrast, on the right side of the diagram, the system can follow any path in the (S,T) plane, so there are infinitely many ways of getting from A to Z, including the simple path A→Z along a contour of constant entropy, as well as more complex paths such as A→Y→Z and A→X→Y→Z. See chapter 19 for more on this. |
| Indeed, there are infinitely many paths from A back to A, such as A→Y→Z→A and A→X→Y→Z→A. Paths that loop back on themselves like this are called thermodynamic cycles. Such a path returns the system to its original state, but generally does not return the surroundings to their original state. This allows us to build heat engines, which take energy from a heat bath and convert it to mechanical work. |
| There are some simple ideas such as specific heat capacity (or molar heat capacity) that can be developed within the limits of cramped thermodynamics, at the high-school level or even the pre-high-school level, and then extended to all of thermodynamics. | Alas there are some other ideas such as “heat content” aka “thermal energy content” that seem attractive in the context of cramped thermodynamics but are extremely deceptive if you try to extend them to uncramped situations. |
Even when cramped ideas (such as heat capacity) can be extended, the extension must be done carefully, as you can see from the fact that the energy capacity CV is different from the enthalpy capacity CP, yet both are widely (if not wisely) called the “heat” capacity.
We do not define entropy in terms of energy, nor vice versa. We do not define either of them in terms of temperature. Entropy and energy are well defined even in situations where the temperature is unknown, undefinable, irrelevant, or zero.
Furthermore, when using partial derivatives, we must not assume that “variables not mentioned are held constant”. That idea is a dirty trick than may work OK in some simple “textbook” situations, but causes chaos when applied to uncramped thermodynamics, even when applied to something as simple as the ideal gas law, as discussed in reference 2. The fundamental problem is that the various variables are not mutually orthogonal. Indeed, we cannot even define what “orthogonal” should mean, because in thermodynamic parameter-space there is no notion of angle and not much notion of length or distance. In other words, there is topology but no geometry, as discussed in section 8.7. This is another reason why thermodynamics is intrinsically and irreducibly complicated.
Uncramped thermodynamics is particularly intolerant of sloppiness, partly because it is so multi-dimensional, and partly because there is no notion of orthogonality. Unfortunately, some thermo books are sloppy in the places where sloppiness is least tolerable.
The usual math-textbook treatment of partial derivatives is dreadful. The standard notation for partial derivatives practically invites misinterpretation.
Some fraction of this mess can be cleaned up just by being careful and not taking shortcuts. Also it may help to visualize partial derivatives using the methods presented in reference 3. Even more of the mess can be cleaned up using differential forms, i.e. exterior derivatives and such, as discussed in reference 4. This raises the price of admission somewhat, but not by much, and it’s worth it. Some expressions that seem mysterious in the usual textbook presentation become obviously correct, easy to interpret, and indeed easy to visualize when re-interpreted in terms of gradient vectors. On the other edge of the same sword, some other mysterious expressions are easily seen to be unreliable and highly deceptive.
Phase space is well worth learning about. It is relevant to Liouville’s theorem, the fluctuation/dissipation theorem, the optical brightness theorem, the Heisenberg uncertainty principle, and the second law of thermodynamics. It even has application to computer science (symplectic integrators). There are even connections to cryptography (Feistel networks).
The term “inexact differential” is sometimes used in this connection, but that term is a misnomer, or at best a horribly misleading idiom. We prefer the term ungrady one-form. In any case, whenever you encounter a path-dependent integral, you must keep in mind that it is not a potential, i.e. not a function of state. See chapter 19 for more on this.
To say the same thing another way, we will not express the first law as dE = dW + dQ or anything like that, even though it is traditional in some quarters to do so. For starters, although such an equation may be meaningful within the narrow context of cramped thermodynamics, it is provably not meaningful for uncramped thermodynamics, as discussed in section 8.2 and chapter 19. It is provably impossible for there to be any W and/or Q that satisfy such an equation when thermodynamic cycles are involved.
Even in cramped situations where it might be possible to split E (and/or dE) into a thermal part and a non-thermal part, it is often unnecessary to do so. Often it works just as well (or better!) to use the unsplit energy, making a direct appeal to the conservation law, equation 1.1.
Heat remains central to unsophisticated cramped thermodynamics, but the modern approach to uncramped thermodynamics focuses more on energy and entropy. Energy and entropy are always well defined, even in cases where heat is not.
The idea of entropy is useful in a wide range of situations, some of which do not involve heat or temperature. As shown in figure 0.1, mechanics involves energy, information theory involves entropy, and thermodynamics involves both energy and entropy.
There are multiple mutually-inconsistent definitions of “heat” that are widely used – or you might say wildly used – as discussed in section 17.1. (This is markedly different from the situation with, say, entropy, where there is really only one idea, even if this one idea has multiple corollaries and applications.) There is no consensus as to “the” definition of heat, and no prospect of achieving consensus anytime soon. There is no need to achieve consensus about “heat”, because we already have consensus about entropy and energy, and that suffices quite nicely. Asking students to recite “the” definition of heat is worse than useless; it rewards rote regurgitation and punishes actual understanding of the subject.