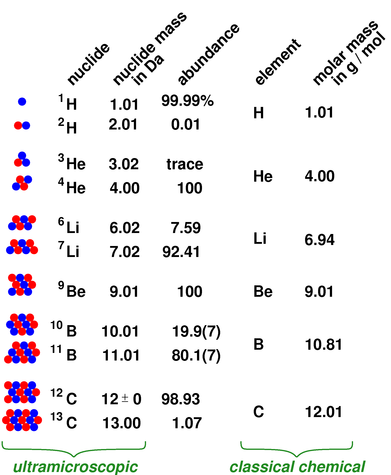
Figure 1: Nuclide, Abundance, Element, and Molar Mass
The notion of atom is absolutely central to chemistry, according to any modern (post-1900) understanding of what chemistry is. This is related to the older notion of chemical element. The best way to define things is to start at the bottom and work our way up, step by step. We start with three fundamental particles (proton, neutron, and electron), then define atom, and then define chemical element.
For present purposes, we consider protons, neutrons, and electrons to be fundamental particles. They are sufficiently fundamental that it is not worth trying to define them in terms of anything more fundamental. As discussed in reference 1, words acquire meaning from how they are used, not from a pithy dictionary-style definition. In that spirit, it suffices to describe the salient properties of these particles.
Each atom has a nucleus consisting of one or more protons and zero or more neutrons. Conventionally, the number of protons is denoted Z, while the number of neutrons is denoted N. Protons and neutrons are both classified as nucleons. (They are the only nucleons you are likely to encounter.)
Each proton carries one unit of positive electrical charge. In contrast, neutrons are electrically neutral. As a result, the nucleus carries exactly Z units of positive electrical charge.
The number Z is called the proton number or synonymously the atomic number.
We name atoms according to atomic number. For example, any atom with Z=1 is called hydrogen by definition, while anything with Z=2 is called helium by definition, et cetera. Any two atoms with the same number of protons (Z) are considered the “same type” of atom, without regard to the number of neutrons (N). This reflects the notion that the chemical properties are determined by Z ... which is true to a decent approximation (but not exactly).
The notion of chemical element is a macroscopic notion (in contrast to atoms, which are ultramicroscopic). Specifically, a chemical element is a collection of atoms, all with the same Z value.
The periodic table (e.g. reference 2) is arranged in order of atomic number. You can find the name of the element corresponding to a particular Z value, and vice versa, using the periodic table. See reference 3 for details on how to think about the periodic table.
If you are going to associate the Z-value with the symbol for an element, the convention is to write it as a subscript to the left of the symbol; for example 2He has Z=2 while 3Li has Z=3. This is of course redundant, since the element-name uniquely specifies the proton number and vice versa. However, sometimes redundancy is good, especially if you don’t have the periodic table memorized or readily accessible.
The highest Z value found on earth in any appreciable quantity is Z=92, which we call uranium. Short-lived radioactive elements can be produced artificially, all the way up to Z=116 the last time I checked.
We can define the nucleon number to be the number of protons plus the number of neutrons. It is denoted A, so we can write A := Z + N by definition.
If you are going to associate the A-value with the symbol for an element, the convention is to write it as a superscript to the left of the symbol; for example 4He has A=4 while 7Li has A=7.
There is no corresponding notation for N. There is no need for it, since if you know Z and A you can instantly infer N, namely N = A − Z.
There are at least two different definitions for the word atom.
This broad definition is particularly convenient when speaking about a collection of atoms, some of which are ionized and some are not. Furthermore, this definition is more-or-less obligatory when speaking about the atoms inside a molecule, where it is usually not possible to keep track of which electrons “belong” to which atom.
If we start with a neutral atom and add or subtract some number of electrons, we create an electrically-charged entity called an ion. The word “ion” also applies to electrically charged molecules.
For most purposes, when people talk about the size and shape of an isolated atom, they mean the size and shape of the atom’s distribution of electrons. This distribution is a somewhat fuzzy cloud. The details of this distribution are formalized in terms of wavefunctions (also sometimes called orbitals) as discussed in reference 4.
Meanwhile, for the atoms inside molecules, any notion of the “size” of an atom is not precise and not particularly useful, because it is not generally possible to keep track of which electrons “belong” to a given atom. Often it is more useful to keep track of the distance between nuclei (rather than atomic “size” per se). Generally this internuclear distance is smaller than you would have guessed based on the “size” of the isolated atom; we can understand by saying there is considerable overlap of the atomic orbitals.
Each proton and each neutron has a mass of very nearly 1 dalton. An electron has a much smaller mass, smaller by a factor of approximately 1836. From this you can infer that nearly all the mass of an atom resides in the nucleus.
The nucleus is tiny, roughly 100,000 times smaller than the overall size of the atom.
Summary:
Tangential remark: Although electrons are found in atoms, that is not the only place they are found. You should not become too enamored of the idea of electrons being attached to a particular atom. That idea is more-or-less OK for isolated individual atoms, but not otherwise. In molecules, the nuclei share one big cloud of electrons. This is quite spectacular in the case of metals and semiconductors, which can be considered enormous macromolecules, with some electron wavefunctions spread across billions upon billions of atoms. Furthermore, you can have electrons running around in free space, e.g. in electronic amplifier tubes and cathode-ray tube (CRT) displays.
In this section, we restrict our attention to ordinary operations involving macroscopic quantities. This means it will be completely impractical to measure quantities by keeping an accurate count of the atoms.
To measure the quantity of a macroscopic sample, often the most precise method is to measure its mass.
| Tangential remark: In Europe, kitchen recipes commonly call for ingredients such as flour, sugar, shortening, etc. to be measured by mass, specified in grams or kilograms. This is accurate and convenient, assuming you have a kitchen scale. | Alas, in the US, kitchen recipes virtually always call for such ingredients etc. to be measured by volume. This is often inaccurate and inconvenient. Switching to European-style recipes would not be easy, because most households in the US don’t even have a kitchen scale. |
For many purposes, we want to be able to prepare samples where the number of atoms is controlled with reasonable precision. For example, this includes setting up chemical reactions so that the stoichiometry comes out right.
In ordinary chemistry-lab situations, it is not convenient to count the atoms one by one. Instead it is appropriate and conventional to scale things by a factor of Avogadro’s constant, which has the value 6.0221415(10)×1023 particles per mole. (In much of Europe this is called Loschmidt’s number, for good reason, as discussed in section 6.4.) The actual definition is arranged so that one mole of isotopically-pure 12C has a mass of exactly 12 grams. As a consequence, a mole of protons has a mass of approximately 1 gram ... more precisely it’s 1.00727646688(13)g.
| Informally, but for all practical purposes, you can think of the concept of mole as follows: It is just a number. A mole is like a dozen, only much larger. We can speak of a dozen carbon atoms, or a mole of carbon atoms. | The formal SI definition of mole is much more abstract. We don’t need to worry about it for present purposes. It will be discussed in section 8. Note that SI is likely to change the definition in the not-too-distant future. |
Note that the practical definition of mole speaks of particles, not atoms. A mole of oxygen atoms weighs about 16 grams, while a mole of oxygen molecules weighs about 32 grams, because the relevant particle is an oxygen molecule (O2) consisting of two oxygen atoms.
To an excellent approximation, the mass of a molecule is the sum of the masses of its constituent atoms. It is traditional in chemistry classes to take this as an exact equality for practical purposes.1
The molar mass of any substance is the average mass per unit number of particles. This concept (and terminology) has a number of advantages:
| Suppose that on average, there are 2.3 children per family. | It is vanishingly unlikely that you will see an “average” family walking down the street with 2.3 children. |
| The molar mass of monatomic Cl (from natural sources) is 35.5 grams per mole, so on average that’s 35.5 dalton per Cl atom. (See section 4 for a discussion of natural abundances.) | You will never find a Cl atom with mass anywhere near 35.5 dalton. (What you actually find is a mixture containing roughly 75% 35Cl and 25% 37Cl.) |
| The molar mass of monatomic Br (from natural sources) is 80 grams per mole, so on average that’s 80 dalton per Br atom. | You will never find in nature a Br atom with mass anywhere near 80 dalton. (What you actually find is a mixture containing roughly 50% 79Br and 50% 81Br.) |
Operationally, the molar mass is determined by measuring each isotope using a high resolution mass spectrometer, and then computing the weighted average (weighted by natural abundance). An example of this calculation is shown in section 4. Additional examples can be found in reference 5.
Students sometimes question whether it is worth knowing the value of Avogadro’s number or (equivalently) the size of atoms. This is a valid, nontrivial question, but the answer turns out to be yes, for reasons discussed in section 6.
It is important to keep in mind that a physical quantity remains the same, no matter what units are used to measure it. For example, the speed of light is the speed of light, no matter whether it is measured in meters per second or furlongs per fortnight. Voltage is voltage, even if it is measured in kilovolts or microvolts. Acreage, otherwise known as area, can be measured in units other than acres. In accordance with this principle, we are not required to measure molar mass in units of grams per mole (although it is commonly convenient to do so).
Dimensionally speaking, the molar mass (regardless of units) has the same dimensions as the so-called «atomic mass» or «average atomic mass» ... but molar mass does a much better job of communicating the concept, especially since for most elements there’s no such thing as an «average» atom.
In addition to the foregoing argument about dimensions, we can make a point about units: one gram per mole is numerically equal to one dalton per particle. So we have here not just equivalent dimensions, but equivalent units. This makes it particularly easy to switch from “average atomic mass” to molar mass. All you need to do is change the name of the table; you don’t need to change the numerical entries in the table.
Here are some units that can be used to measure molar mass:
Here are some terms and concepts that you may encounter:
The bottle is almost certainly labelled «SiO2» even though the molecules in the bottle are 15 or 20 orders of magnitude bigger than that. The «formula weight» on the label corresponds to the mass of the hypothetical monomer, not the macromolecules.
Similar words apply to a bottle of chemically-pure iron filings. Each particle is a macromolecule. The bottle is almost certainly labeled «Fe», even though the molecules in the bottle are many many orders of magnitude larger than that.
In any case, whatever you decide the “empirical formula” is, you are better off thinking and speaking in terms of formula mass, or (even better) empirical formula mass.
We now turn from discussing macroscopic collections of atoms and molecules to discussing individual atoms and their nuclei.
Disclaimer: you shouldn’t need to deal with individual atoms in order to do intro-level chemistry. Almost all chemistry (especially intro-level chemical reaction work) deals with macroscopic samples, i.e. with samples where the atom-count is closer to 1023 than it is to 1. Therefore the molar mass, as given in the periodic table, is sufficient information to let you get on with your work, even though it may be less than sufficient to satisfy your curiosity about individual atoms, and/or about non-chemical processes such as radioactive decay.
Recall that an atomic nucleus is composed of Z protons and N neutrons.
A particular value of the pair (Z, N) defines our notion of nuclide. (This is analogous to the way a Z-value defined our notion of chemical element.)
In addition to the nucleon number (A = Z + N), we should discuss a related concept and some related terminology:
| Baryon number is conserved, even in exotic non-chemical situations where nucleon number is not. That’s because there exist baryons other than nucleons. | In ordinary chem-lab processes, including radioactive decay, nucleons are the only baryons you will encounter, in which case the nucleon number is essentially conserved, because it is essentially equal to the baryon number. |
To denote a nuclide, the conventional notation is to write the A-value as a superscript to the left of the symbol corresponding to the Z-value. For example, 3He has one neutron and two protons, for a total of three nucleons. The neutron number (N) is rarely written down explicitly; you are expected to infer it from the nucleon number (A) and the proton number (Z).
Each nuclide (Z, N) is considered an isotope of the corresponding chemical element (Z). For example, 4He is the most-common isotope of He. By extension, two nuclides with the same Z value are called isotopes of each other. For example, 3He is called an isotope of 4He and vice versa.2
Protons and neutrons each have a molar mass close to 1 dalton, and other contributions to the mass of the nuclide are small in comparison. Therefore, for example, 4He will have a molar mass close to 4 grams per mole.
| If you know the nucleon number of a nuclide, you can infer its molar mass to a good approximation. Conversely, if you know the molar mass of a nuclide, you can infer its nucleon number exactly. | If you know the molar mass of a chemical element, do not try to infer “the” nucleon number or even the “typical” nucleon number. It cannot be done reliably. Counterexamples abound, such as chlorine and bromine, as discussed in section 2.1. |
| Nuclides, yes. | Elements, no. |
The situation for the first few elements is shown in figure 1.
For clarity, the numbers in the figure have been rounded off, keeping only enough precision to make the point about molar mass being a weighted average of the nuclide masses. With the exception of the boron abundances, the numbers are known to considerably more precision than this. For details, see the references (section 9).
Qualifiers such as “natural” or “naturally-occurring” appear over and over again in this document, because it is possible to obtain samples that don’t have the natural distribution of isotopes. It is easy to buy a mole of 3He, although it is more expensive than ordinary 4He. Similarly it is easy to buy a mole of heavy water (D2O), although it is more expensive than ordinary water. In seawater, there is roughly one deuterium atom for every 6500 hydrogen atoms. You can shift this quite a bit in either direction by fractional distillation or gaseous diffusion. This can even happen inadvertently.
The natural product is not always cheaper; natural uranium (which contains about half a percent of 235U) is much more valuable than depleted uranium (from which most of the 235U has been removed).
Therefore, if you want to speak clearly, you can’t simply talk about the molar mass of this-or-that element; you need to specify that you’re talking about the molar mass of the naturally occurring element.
However, even that isn’t entirely sufficient. It is possible to find different natural sources with different distributions of isotopes. So if you want to be really precise, you need to specify the source: e.g. seawater (not just natural water), or atmospheric nitrogen (not just natural nitrogen).
Usually, if you just grab a stock-bottle from the stockroom, the molar mass will be very close to the conventonal “textbook” value, close enough for most purposes. However, for high-precision work, you should double-check the label of the stock-bottle, to make sure the molar mass specified on the label is what you were expecting. In particular, commercially available lithium compounds are sometimes significantly depleted of 6Li, leading to an unnaturally high molar mass (reference 6).
The molar mass of a natural sample of a chemical element can be expressed as a weighted average of the isotopes of that element, weighted by their natural abundance. The molar mass of each isotope, along with the natural abundance, can be obtained from the table of nuclides (reference 7), although sometimes more accurate abundance data can be obtained from reference 8.
| molar mass | natural | ||||
| / dalton | abundance | ||||
| 35Cl | 34.96885 | × | 75.78% | = | 26.4994 |
| 37Cl | 36.96590 | × | 24.22% | = | 8.95314 |
| ——— | |||||
| average: | 35.453 |
| nuclide mass | natural | ||||
| / dalton | abundance | ||||
| 79Br | 78.9183376(20) | × | 50.686(26)% | = | 40.00055 |
| 81Br | 80.9162911(30) | × | 49.314(26)% | = | 39.90306 |
| ——— | |||||
| average: | 79.90361(52) |
The bromine molar mass computed here is reasonably consistent with the values given in the Los Alamos periodic table (reference 2), namely 79.904(1). Their error bars are twice as large. Perhaps they are using older data, or perhaps they are accounting for sources of uncertainty that I am overlooking.
It is worth emphasizing that the molar mass of natural Br is 80, even though the nuclide 80Br has zero natural abundance. It can be created artificially, but it is radioactive with a short half-life, as you can ascertain from the table of nuclides (reference 7).
To repeat:
| Yes, given the masses and abundances of the nuclides, you can compute the molar mass of the element, by a process of averaging. | No, given the molar mass of the element, you cannot reliably undo the averaging to obtain the nucleon numbers, nuclide masses, or abundances. |
For most elements, uncertainty as to the natural abundances is the dominant contribution to the overall uncertainty of the element’s molar mass (far greater than the contribution from the uncertainty in the mass of each isotope). However, there are 21 elements in the periodic table for which only one isotope is found in nature. The molar mass of these elements is known to dramatically greater precision, compared to other elements, because there is no uncertainty as to the natural abundance.
Some quantum-mechanical calculations are very easy to do. Let’s see if we can calculate a rough estimate for the size of a hydrogen atom. We anticipate that our answer should come out close to the famous Bohr radius, namely:
| (1) |
where 4 π є0 is the constant that appears in Coulomb’s law of electrostatics; ℏ is Planck’s constant, e is the elementary charge; and m is the electron mass. See item 5 for more discussion of these quantities.
Our estimate will use little more than dimensional analysis. The electron in the atom can be roughly approximated as a particle in a box, or (equivalently) a wave in a box.3 Some standing-wave wavefunctions for the one-dimensional particle in a box are shown in figure 2.
We proceed by applying the following equations. With the possible exception of equation 2a, these equations should be familiar from high-school physics:
|
where k is the wavenumber and Λ is the wavelength.
To proceed, we set PE=KE ... by dimensional analysis (or by the virial theorem, if you want to be fancy). We then have
| (3) |
which is the same as equation 1 except for an extraneous factor of π2/8. This is as close as one could hope to get by means of dimensional analysis. (Note that Bohr’s formula – equation 1 – was only an approximation to begin with.) Also note that we include an explicit factor of Z, to cover hydrogenic (single-electron) species other than hydrogen, such as He+ and Li++.
We can understand what’s happening in the following terms: The electrostatic interaction (equation 2d) keeps the atom from getting too big, while the kinetic energy associated with the stress of bending the wavefunction (equation 2c) keeps the atom from getting too small. It must be emphasized that without the quantum mechanical kinetic energy, the atom would collapse. The electron would spiral down into the nucleus, leaving the atom several orders of magnitude smaller than the observed size. This is just one of many reasons why we say:
This is cloned from a proverb about another exceedingly successful theory:
Sometimes people ask how we “really” know that atoms exist, how we “really” know the size of atoms, and why we should care. These are nontrivial questions, for reasons discussed in section 6.2. Many things that we see in our daily lives are sensitive to the size of atoms, but the dependence may not be immediately obvious.
Ask yourself: If atoms tomorrow were ten times bigger than today, would you notice? How would you notice? What would you look for?
Here are some possible answers. The ☞☜ symbol indicates a “hands on” experiment that can be done with simple apparatus.
I don’t want to get into a metaphysical debate over whether the bumps seen in figure 3 “are” atoms. It suffices to say that the bumps are in one-to-one correspondence with atoms, and that the spacing of the bumps tells us the spacing of the atoms.
|
A mass spectrometer operates directly on atoms, smallish
molecules, and smallish fragments of larger molecules. It classifies
them according to their charge-to-mass ratio, to high precision. For
example, it can easily distinguish 79Br from 81Br, and tell
you that no 80Br is present. There are dozens of different types
and subtypes of mass spectrometers. The canonical types look at the
curved trajectory of charged particles moving in a magnetic field.
See reference 10.
|
It is not hard to get electronics that is sensitive enough to
respond to single electrons. From this you can immediately determine
the number of elementary charges in a coulomb, thereby connecting the
microscopic world to the macroscopic world. Even when you are not clearly seeing individual electrons, you might see shot noise, which is sensitive to the size of electrons. |
| Good e-over-m can also be obtained from electrochemistry (electroplating, electrolysis, et cetera). | The classic Millikan experiment will also give you the value of the elementary charge. |
Note that Coulomb’s constant can be determined by measuring a capacitor; Planck’s constant can be determined via the black-body radiation formula and/or via the photoelectric effect; the elementary charge can be measured in various ways as discussed in item 3, and the electron mass can be obtained from e/m data, which in turn can come from electrons moving in a magnetic field. You don’t need to measure all of these things at once, but the point is that you could measure them, so you don’t need to take anything on faith.
☞☜ There is a simple widely-known high-school chemistry experiment that involves HCl diffusing in one direction and NH3 diffusing in the other direction in a tube, roughly 1 meter long and 1 cm in diameter. This (plus some algebra) provides rather decent quantitative information about the size of the molecules involved. With a little more effort, you can do this as a function of pressure, which provides a powerful way of verifying that mean free path and cross section are behaving as advertised.
Historical remark: Avogadro died without ever knowing the value of Avogadro’s number, not within several orders of magnitude in either direction. It fell to Loschmidt to make the first serious measurement, based on transport data (speed of diffusion versus speed of sound).
☞☜ Thermal conductivity is rather easy to measure. Take care to prevent convection.
☞☜ There are several ways to measure the viscosity. One amusing way is by looking at the damping of sound waves in a closed resonator.
Historical remark: Brownian motion played a role in the history of science, providing some relatively early, relatively convincing evidence for the size of atoms. The medium-small Brownian particle serves as bridge between our macroscopic world and the ultramicroscopic world of atoms and molecules. See reference 14 and reference 15.
Observation of Brownian motion is well within the capabilities of high-school or even elementary-school students. Getting from the raw observation to a quantitative determination of the size of molecules requires more analysis than young kids can handle, but the raw data provides at least some glimmer of an appreciation for what is going on in the microscopic and submicroscopic realms.
Note that several of the items on this list fall into a pattern:
| In gases, there are a number of first-order properties that don’t tell you much about the size of atoms. These include pressure, temperature, compressibility, speed of sound, et cetera. | There are a number of second-order properties and transport properties that do directly depend on the size of atoms and on the spacing between atoms (or molecules). These include thermal conductivity, viscosity, diffusion, and the fluctuations in various first-order quantities. |
We define the weak atomic hypothesis to be the hypothesis that atoms exist, and have some smallish but nonzero size. That is, we hypothesize that Avogadro’s number “exists” in some vague sense. We consider it large but finite, without bothering to ascertain an accurate value.
There are many important chemistry and physics experiments that provide good evidence for the weak atomic hypothesis. They provide evidence that atoms exist, but do not tell us anything about the size of atoms. Examples include:
Also, this experiment by itself doesn’t say anything about the number of atoms per molecule. To get that information you need to do additional experiments, perhaps as discussed in the next item.
This requires you to get the chemical formulas right. As an example of what can go wrong, if you think the natural oxide of X is XO when in fact it is XO2, you will get the molar mass of X wrong by a factor of two.
This law was important in the history of chemistry. It predates the periodic table, and helped lay the groundwork for it.
This doesn’t require any notion of stoichiometry, and doesn’t even require you to have a correct chemical formula. That’s important, because almost none of the solids you see around you have a definite formula, i.e. none of them uphold Dalton’s so-called law of multiple proportions. This includes glass, ceramics, most metal objects, most plastic objects, wood, animal hair and tissue, minerals such as feldspar, et cetera.
At low temperatures, the law of Dulong and Petit fails. Nowadays the solution is to use something like the Debye model, which works well at low temperatures and correctly reproduces the law of Dulong and Petit at high temperatures.
Both these models (Debye and Dulong/Petit) deal only solids and deal only with the part of the specific heat that is due to phonons, i.e. the “lattice” specific heat. They leave out contributions from spin degrees of freedom, electrons, crystallographic phase changes, etc., which are sometimes very significant.
Suppose you have established the weak atomic hypothesis. Further suppose you have measured lots of stoichiometric ratios using the methods enumerated above. Then, if you discover the size of one type of atom, you can figure out the size of all the others. The process works like this: The size of one atom plus stoichiometry tells you the size of another, and then you iterate until you have a complete table.
By way of contrast to the strong atomic hypothesis (section 6.1) and even the weak atomic hypothesis (section 6.2), there are quite a few things that can be adequately explained in terms of a continuous fluid, without any need to mention atoms. Examples include
We use the term hydrodynamic limit or hydrodynamic approximation to refer to situations where the phenomena of interest are well described by macroscopic properties, such as those listed above. Such situations commonly arise when the length-scale of interest is huge compared to the size of particles and huge compared to the spacing between particles.
It may be possible to derive and explain the macroscopic properties in terms of atomic theory, but once we have done so (or even if we haven’t), we don’t need to keep track of individual atoms, because the macroscopic properties tell us what we need to know, in the hydrodynamic limit.
The hydrodynamic approximation works well in almost all everyday situations, which is not surprising given how small atoms are. For thousands of generations, people were able to live their lives without knowing anything about atoms.
Transport properties such as viscosity and diffusion are not included in the list above, because they are in a slightly different category. Without transport properties, the items on the list (indiviually and collectively) do not provide a sufficient basis for ascertaining the size of atoms. In contrast, if you add diffusion and/or viscosity to the list, you then have enough information to estimate the size of atoms, as Loschmidt did (reference 13).
On the other hand, if you don’t accept the atomic hypothesis, you can introduce viscosity etc. into the hydrodynamic equations on an ad-hoc macroscopic basis. The equations were known for many years before anybody realized what they implied about atoms.
Amedeo Avogadro died without ever knowing the value of Avogadro’s number. If you had guessed a number 100 times too big or 100 times to small, he would have been unable to refute your guess. Johann Loschmidt is generally credited with the first scientific measurement of the size of atoms (reference 13). In much of Europe, the thing we call Avogadro’s number is called Loschmidt’s number, which makes a certain amount of sense. Beware that in the US, the same term, Loschmidt’s number, is on rare occasions used with a different but closely-related meaning, namely the number of particles in one cm3 of gas at standard temperature and pressure.
The terms “atomic mass”, “relative atomic mass”, and “atomic weight” are deprecated; use molar mass instead.
Any terms involving atomic “weight” are deprecated; use the corresponding notions of mass instead.
The terms “mass number” and “atomic mass number” are deprecated; use nucleon number (aka baryon number) instead.
The typical periodic table gives you the molar mass, which is sufficient for doing ordinary chem-lab experiments with macroscopic samples. If you are curious about isotopes, the ordinary periodic table does not suffice; you need a chart of the nuclides.
If you want the formal SI definition of mole, here it is:
1. The mole is the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon 12; its symbol is "mol".
The advantages and disadvantages of this definition can be summarized as follows:
| Pro | Con |
| The definition given above is a direct quote from the SI document, reference 19. | The SI definition doesn’t explain what they mean by “substance” or “amount of substance”. |
| The notion of “amount of substance” was important in the history of chemistry. It is a macroscopic 19th-century concept. It predates any knowledge of the numerical value of Avogadro’s number ... just as the macroscopic 19th-century notions of element and compound predate the modern microscopic notions of atom and molecule. | In a modern context, defining a mole as “amount of substance” is less useful, harder to understand, and no more precise, compared to the practical numerical definition given in section 2.1. |
| Some chemistry teachers vehemently insist on this definition, and object to treating a mole as a number (as we did in section 2.1). | The definition of mole is a moving target. In the metrology community, there are serious efforts toward redefining it to be an exact pure number. (This is analogous to the process whereby the speed of light was redefined to have an exact value.) |
Bottom line: For practical purposes, the modern notions are simpler and in all ways better.
English translation: “On the Size of the Air Molecules”
J. Chem. Educ. 72 (10), p 870 (1995).
http://pubs.acs.org/doi/abs/10.1021/ed072p870.2