Uncertainty
as Applied to
Measurements and Calculations
John Denker
1 Introduction
1.1 How Many Digits Should Be Used?
Here are some simple rules that apply whenever you are writing
down a number:
-
-
Use many enough digits to avoid unintended loss of
information.
-
Use few enough digits to be reasonably convenient.
| Important note: The previous two
sentences tell you everything you need to know for most purposes,
including real-life situations as well as academic situations at
every level from primary school up to and including introductory
college level. You can probably skip the rest of this document. |
-
When using a calculator, it is good practice
to leave intermediate results in the machine. This is
simultaneously more accurate and more convenient than writing them
down and then keying them in again. For details on this, see
section 7.11.
Seriously: The primary rule is to use plenty of digits. You hardly
even need to think about it. Too many is vastly better than too few.
To say the same thing the other way: If you ever have more digits than
you need and they are causing major inconvenience, then you can
think about reducing the number of digits.
If you want more-detailed guidance, some ultra-simple procedures are
outlined in section 2. If you want even more guidance,
the details on how to do things right are discussed in section 8.2.
For a discussion of the effect of roundoff, see section 8.6. For a discussion of why using “sig figs” is
insane, see section 1.3. There is also a
complete table of contents.
1.2 What About Uncertainty?
-
In many cases, when you write down a number,
you need not and should not associate it with any notion of
uncertainty.
-
One way this can happen is if you have a number
with zero uncertainty. If you roll a pair of dice and observe five
spots, the number of spots is 5. This is a raw data point, with no
uncertainty whatsoever. So just write down the number. Similarly,
the number of centimeters per inch is 2.54, by definition, with no
uncertainty whatsoever. Again: just write down the number.
-
Another possibility is that there is
a cooked data blob, which in principle must have “some” uncertainty,
but the uncertainty is too small to be interesting. It is
insignificant. It is unimportant. It is immaterial. There are
plenty of situations a moderately rough approximation is sufficient.
There are even some situations where an extremely rough
approximation is called for, as in so-called “Fermi” problems. This
point is discussed in reference 1.
Along the same lines, here is a less-extreme example that arises in
the introductory chemistry class. Suppose the assignment is to
balance the equation for the combustion of gasoline, namely
|
a C8H18 + b O2 | | → | | x CO2 + y H2O
|
| (1)
|
by finding numerical values for the coefficients a, b, x, and
y. The conventional answer is (a, b, x, y) = (2, 25, 16, 18).
The outcome of the real reaction must have “some” uncertainty,
because there will generally be some nonidealities, including the
presence of other molecules such as CO or C60, not to
mention NO2 or whatever. However, my point is that we don’t
necessarily care about these nonidealities. We can perfectly well
find the idealized solution to the idealized equation and postpone
worrying about the nonidealities and uncertainties until much, much
later.
As another example, suppose you use a digital stopwatch to measure
some event, and the reading is 1.234 seconds. We call this number the
indicated time, and we distinguish it from the true time
of the event, as discussed in section 5.5. In
principle, there is no chance that the indicated time will be exactly
equal to the true time (since true time is a continuous variable,
whereas the indicated time is quantized). However, in many cases you
may decide that it is close enough, in which case you should just
write down the indicated reading and not worry about the quantization
error.
-
The best way to understand
uncertainty is in terms of probability distributions. Such
things are discussed in section 3.1 and in more detail
in reference 2.
-
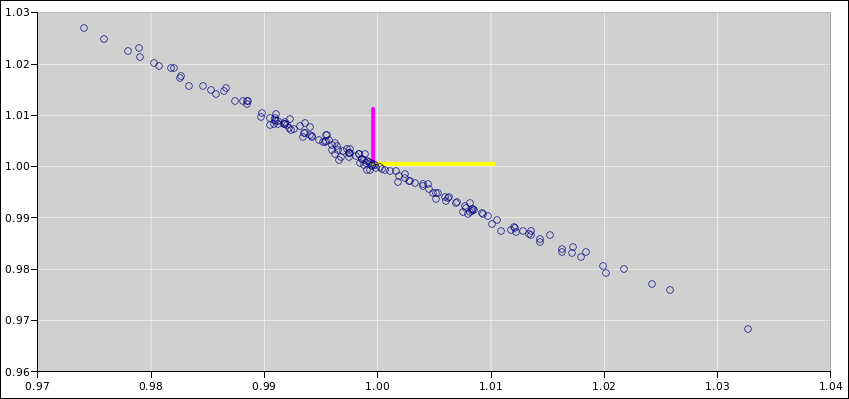
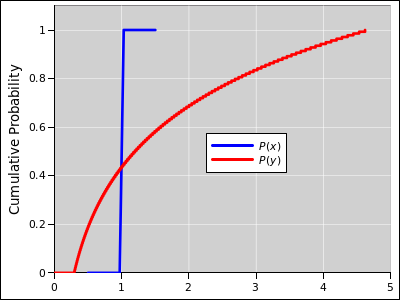
Suppose we wish to describe a probability
distribution, and further suppose it is a simple one-dimensional
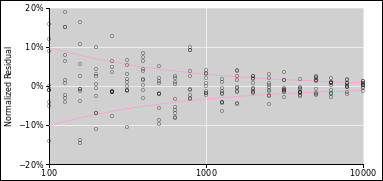
distribution, such as the one shown in figure 1. (There’s a lot going on in this figure; for
details, see reference 2.) Any Gaussian
distribution (also called a normal distribution, or simply a
Gaussian) can be described in terms of two numbers, namely the nominal
value and the uncertainty. One good notation for this uses an
expression of the form 1.234 ± 0.055, where the first numeral
(in this case 1.234) represents the nominal value, and the second
numeral (in this case 0.055) represents the width of the distribution,
i.e. the absolute uncertainty. (Typically, but not necessarily, the
standard deviation is used to quantify the width. The region
spanned by ± one standard deviation, i.e. ± 0.055, is
indicated by yellow shading in the diagram.) This notation works for
algebraic symbols, too: A±B.
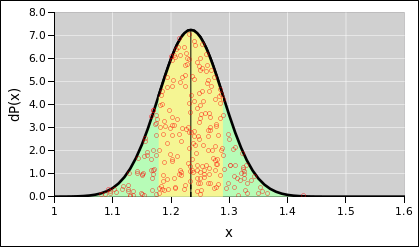 Figure 1
Figure 1: Gaussian Distribution, 1.234±0.55
For numerical (non-algebraic) values, you can write something of the
form 1.234(55), where the number in parentheses indicates the
uncertainty. The place-value is such that the last digit of the
uncertainty lines up with the last digit of the nominal value.
Therefore 1.234(55) is just a more-compact way of writing 1.234 ±
0.055.
When a number has been subjected to rounding, the roundoff error is at
most a half-count in the last decimal place. If this is the dominant
contribution to the uncertainty, we can denote it by 543.2[½].
Beware that the distribution of roundoff errors is nowhere near
Gaussian, as discussed in section 8.3.
In cases where you are uncertain about the uncertainty, as sometimes
happens, you can write 543.2(x) which represents a “few” counts of
uncertainty in the last place. This stands in contrast to 543.2(?)
which usually means that the entire value is dubious, i.e. some
chance of a gross error (such as measuring the length instead of the
width).
If you wish to describe the uncertainty in relative terms (as opposed
to absolute terms), it can be expressed using percentages, parts per
thousand, parts per million, or something like that, e.g. 2900 ±
0.13% or equivalently 2900 ± 1300ppm.
(Note that in the expression 1.234 ± 0.055 we have two separate
numbers represented by two separate numerals, which makes sense. This
stands in contrast to the “sig figs” notation, which tries to
represent two numbers using a single numeral, which is a very bad
idea.)
-
Suppose we have a distribution over x and a
distribution over y. If the two distributions are known to be
uncorrelated, you can get away with describing each one
separately, with one nominal value and one width apiece. However,
that only works in certain special situations. More generally, you
need to talk about the distribution over x and y jointly. Knowing
the width in the x-direction and the width in the y-direction is
nowhere near sufficient to give a complete description of the joint
distribution, because correlations can produce an elongated, cockeyed
distribution, as in figure 2. For details, see
section 7.7, section 7.23, and
section 9.3.
|
If you have N variables that are statistically independent
and Gaussian distributed, you can describe the uncertainty in terms of
N variances. (The standard deviation is the square root of the
variance.)
|
|
If you have N variables that are correlated, to describe
an N-dimensional Gaussian distribution requires a covariance
matrix which has N2 entries. The plain old variances are the
diagonal elements of the covariance matrix, and they don’t tell the
whole story, especially when N is large.
|
In the real world, there are commonly nontrivial correlations
involving several variables – or several thousand variables. In
other words, there are lots of nontrivial off-diagonal matrix elements
in the covariance matrix.
As a corollary, you should not become too enamored of the notation
1.234 ± 0.055 or 1.234(55), because that only allows you to
keep track of the N variances, not the N2 covariances.
-
Let us continue with the stopwatch example that was
introduced in item 4. Suppose we make two
observations. The first reading is 1.234 seconds, and the second
reading is just the same, namely 1.234 seconds. Meanwhile, however,
you may believe that if you repeated the experiment many times, the
resulting set of readings would have some amount of scatter, namely
± 0.01 seconds. The two observations that we actually have don’t
show any scatter at all, so your estimate of the uncertainty remains
hypothetical and theoretical. Theoretical information is still
information, and should be written down in the lab book, plain and
simple. For example, you might write a sentence that says “Intuition
suggests the timing data is reproducible ± 0.01 seconds.” It
would be even better to include some explanation of why you think so.
The principle is simple: Write down what you know. Say what you mean,
and mean what you say.
-
The same principle applies to the indicated
values. The recommend practice is to write down each indicated value,
as-is, plain and simple.
You are not trying write down the true values. You
don’t know the true values (except insofar as the indicated values
represent them, indirectly), as discussed in
section 5.5. You don’t need to know the true
values, so don’t worry about it. The rule is: Write down
what you know. So write down the indicated value.Also: You are not obliged to attribute any uncertainty to the
numbers you write down. Normal lab-book entries do not express an
uncertainty using A±B notation or otherwise, and they do not
“imply” an uncertainty using sig figs or otherwise. We are
always uncertain about the true value, but we aren’t writing down
the true value, so that’s not a concern. For an example of how
this works, see table 5 in section 6.4.
Some people say there must be some uncertainty “associated” with
the number you write down, and of course there is, indirectly, in
the sense that the indicated value is “associated” with some
range of true values. We are always uncertain about the true
value, but that does not mean we are uncertain about the indicated
value. These things are “associated” ... but they are not the
same thing.
In a well-designed experiment, things like readability and
quantization error usually do not make a large contribution to the
overall uncertainty anyway, as discussed in
section 5.8. Please do not confuse such things
with “the” uncertainty.
-
There must be some “calibration rule” that
connects each indicated value to the corresponding range of true
values. Be sure to write this rule in the lab book somewhere, unless
it is super-obvious.
It suffices to write down the rule just once; you do not need to
restate the rule every time you take a reading. Later, when you are
analyzing the data, you can apply the rule to each of the
readings.1 As a familiar
example of such a rule, you might say “all readings are uncertain due
to Poisson statistics”. For another familiar example, see
section 6.1.
-
Before you report “the” uncertainty in
your results, make sure you have identified all significant
contributions to the uncertainty. It does no good to carefully
calculate one contribution while overlooking other contributions.
See section 5.8. Also, watch out for correlated
uncertainties. See section 7.18.
-
When describing a distribution, state what family of
distributions you are talking about, unless this is obvious from
context. Examples include Gaussian, square, triangular, Bernoulli,
Poisson, et cetera. See section 8.5 and section 13.8 for
why this is important. See reference 2 for a
discussion of some common distributions, and the relationships
between them.
-
It is usually a good practice to keep all the
original data. When reading an instrument, read it as precisely as
the instrument permits, and write down the reading “as is”
... without any conversions, any roundoff, or anything else. See
section 8.4 for details (including the rare and tricky
possible exceptions).
1.3 What About Significant Figures?
-
No matter what you are trying to do,
significant figures are the wrong way to do it.
When writing, do not use the number of digits to imply anything about
the uncertainty. If you want to describe a distribution, describe it
explicitly, perhaps using expressions such as 1.234±0.055, as
discussed in section 1.2.
When reading, do not assume the number of digits tells you anything
about the overall uncertainty, accuracy, precision, tolerance, or
anything else, unless you are absolutely sure that’s what the writer
intended ... and even then, beware that the meaning is very unclear.
|
People who care about their data don’t use sig figs.
|
|
|
|
Significant-digit dogma destroys your data and messes up your thinking
in many ways, including:
- Given a distribution that can be described by an expression such
as A±B, such as 1.234±0.055, converting it to sig figs
gives you an excessively crude and erratic representation of the
uncertainty, B. See section 8.6.3 and especially
section 17.5.
- Converting to sig figs also causes excessive roundoff error in
the nominal value, A. This is a big problem. See section 7.12 for a concrete example.
- Sig figs cause people to misunderstand the distinction between
roundoff error and uncertainty. See section 7.12 and
section 6.4.
- Sig figs cause people to misunderstand the distinction between
uncertainty and significance. See section 14,
especially section 14.3.
- Sig figs cause people to misunderstand the distinction between
the indicated value and the corresponding range of true
values. See section 5.5.
- Sig figs cause people to misunderstand the distinction between
distributions and numbers. Distributions have width, whereas numbers
don’t. Uncertainty is necessarily associated with some distribution,
not with any particular point that might have been drawn from the
distribution. See section 3.1, section 6.4, and reference 2.
- As a consequence, sig figs make people hesitate to write down
numbers. They think they need to know the amount of supposedly
“associated” uncertainty before they can write the number, when in
fact they don’t. Very commonly, there simply isn’t any
“associated” uncertainty anyway, as discussed in item 4.
- Sig figs weaken people’s understanding of the axioms of the
decimal numeral system. See section 17.5.7.
- Sig figs provide no guidance as to the appropriate decimal
representation for repeating decimals such as 80 ÷ 81, or
irrational numbers such as √2 or π.
- Sig figs give people the idea that N nominal values should be
associated with N uncertainties, which is just crazy. In fact the
number of uncertainties scales like (N2 + N)/2, as discussed in
section 9.3.
- As a related point, sig figs is predicated on «propagation of
error» which in turn assumes that things are uncorrelated, when in
fact there are often lots of correlations. This causes the
error-estimates to fail without warning.
- The sig figs approach cannot possibly apply to algebraic
variables such as A±B, so you are going to have to learn the
A±B representation anyway. Having learned it, you might as
well use it for decimal numerals such as 1.234±0.055. See
section 17.5.5.
- Sig figs cause people to misunderstand the distinction between
representation of uncertainty and propagation of
uncertainty. See section 7.1.
- Et cetera
For a more detailed discussion of why sig figs are a bad idea, see
section 17 and reference 3
2 Pedagogical Digression – Extreme Simplifications
2.1 Postponing Uncertainty
In an introductory chemistry class, you should start with some useful
chemistry ideas, such as atoms, molecules, bonds, energy, atomic
number, nucleon number, etc. — without worrying about
uncertainty in any form, and double-especially without introducing
ideas (such as sig figs) that are mostly wrong and worse than useless.
Roundoff procedures are necessary, so learn that. Scientific notation
is worthwhile, so learn that. The “sig figs” rules that you find in
chemistry books are not necessary and are not worthwhile, so the less
said about them, the better.
In place of the “sig figs” rules, you can use the following
guidelines:
-
Keep all the original data. Do not round off the
original data. See item 13 above.
- In the introductory class, the following “house rules”
apply:
Basic 3-digit rule: For a number in scientific notation, the rule
is simple: For present purposes, you are allowed to round it off to
three digits (i.e. two decimal places).
Example: 1.23456×108 may be rounded to 1.23×108
For a number not in scientific notation, the rule is almost as
simple: convert to scientific notation, then apply the
aforementioned 3-digit rule. (Afterwards, you can convert back, or
not, as you wish.)
The point of these rules is to limit the amount of roundoff error.
As a corollary, you are allowed to keep more than three digits if
you wish, for any reason, or for no reason at all. This is makes
sense because it introduces even less roundoff error. As another
corollary, trailing zeros may always be rounded off, since that
introduces no roundoff error at all.
Example: 1.80 may be rounded to 1.8, since that means the same
thing. Conversely 1.8 can be
represented as 1.80, 1.800, 1.8000000, et cetera.
These rules apply to intermediate steps as well as to final results.
These “house rules” apply unless/until you hear otherwise. They
tell you what is considered significant at the moment. As such,
they have zero portability outside the introductory class, and even
within this class we will encounter some exceptions (as in
section 7.8 for example). Still, for now three digits
is enough. There is method to this madness, but now is not the
time to worry about it. We have more important things to worry
about.
These rules differ in several ways from the “sig figs” rules that
you often see in introductory chemistry textbooks.
Remember, these are roundoff rules. Do not confuse roundoff
with uncertainty. Roundoff error is just one contribution to the
overall uncertainty. Knowing how much roundoff has occurred gives you
a lower bound on the overall uncertainty, but this lower bound is
rarely the whole story. Looking at the number of digits in a numeral
gives you an upper bound on how much roundoff has occurred. (This is
not a tight upper bound, since the number might be exact, i.e. no
roundoff at all.) At the end of the day, the number of digits tells
you nothing about the overall uncertainty.
Roundoff error is in the category of things that we generally do not
need to know very precisely, so long as it is small enough.
Uncertainty is not in this category, for reasons discussed in
section 4.4.
2.2 Range of Numbers (as a Simplified Distribution)
As discussed in section 3.1, an expression such as
1.234±0.055 does not represent a number, but rather a distribution
over numbers, i.e. a probability distribution. Unfortunately, people
sometimes use sloppy shorthand shorthand expressions, perhaps
referring to the «random variable» x or the «uncertain quantity»
x, such that x = 1.234±0.055. Beware that this shorthand causes
endless confusion. When in doubt, it is best to think of
1.234±0.055 as describing a distribution.
As a compromise, in the all-too-common situation where somebody wants
to learn about uncertainty but doesn’t have a very strong background in
probability, we can simplify things by talking about an interval
or equivalently a range of numbers.
Note: “interval” is an official mathematical
term, while “range of numbers” is more likely to be
understood by non-experts.
Working with intervals is easier than working with distributions. You
can draw a range of numbers on the number line much more easily
than you can draw a probability distribution. It is not an ideal
solution, but it is a way to get started. (In contrast, the idea of
so-called «random variables» is not good, not as a starting point or
anything else.)
In order of decreasing power, sophistication, and reliability:
|
probability distributions
≫ intervals ≫ so-called «random variables»
(2) |
In order of decreasing simplicity:
|
intervals ≫ probability distributions
≫ so-called «random variables»
(3) |
In any case, the fundamental point is that some situations cannot be
described by a single “number”. Instead, they are better described
by a whole range of numbers that are consistent with our
knowledge of the situation. The extent of the range expresses the
uncertainty. One way to explain this is in terms of hedging a bet. If
you roll a pair of dice, the most likely outcome is 7 ... but that
outcome occurs less than 17% of the time. If you want to be right
more than half of the time, you can’t do it by betting on any single
number, but you can do it by betting on a range of numbers.
So, if you want, you can simplify the following discussion (with only
a modest reduction in correctness) by crossing out every mention of
“probability distribution” and replacing it with “range of
numbers”.
* Contents
3 Foundations and Prerequisites
3.1 What Is Uncertainty?
The best way to understand uncertainty is in terms of probability
distributions. The idea of probability is intimately connected with
the idea of randomness.
The make use of this idea, you have to identify the relevant ensemble,
i.e. the relevant probability distribution, i.e. the relevant
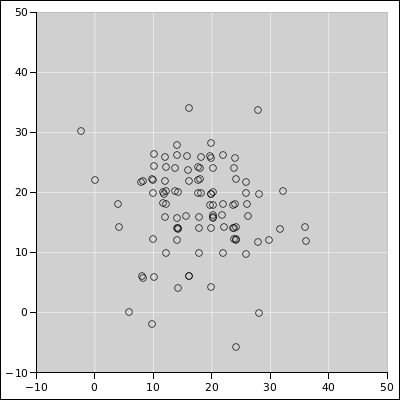
probability measure. Consider for example the star cluster shown in
figure 3. There are two ways to proceed:
- Distribution (A)
- You could pick one particular star
and re-measure its celestial coordinates again and again. This would
produce a sample with some tiny “error bars”.
- Distribution (B)
- You could randomly pick various
stars from the cluster and measure the coordinates of each one.
These are both perfectly good distributions; they’re just not the same
distribution. There are innumerable other distributions you could
define. It is often nontrivial to decide which distribution is most
informative in any given situation. There is no such thing as «the»
all-purpose probability distribution.
To calculate the width of the cluster in figure 3, the conventional and reasonable approach
is to measure a great many individual stars and then let the data
speak for itself. Among other things, you could calculate the mean
and standard deviation of the ensemble of star-positions.
In contrast, you cannot use the width of distribution (A) to infer
anything about the width of distribution (B). You could measure each
individual star ten times more accurately or ten times less accurately
and it would have no effect on your value for the width of the
cluster. Therefore the whole idea of “propagation of uncertainty”
is pointless in this situation.
 Figure 3
Figure 3: M13 Globular Cluster in Hercules
(Brian McLeod, Harvard-Smithsonian Center for Astrophysics)
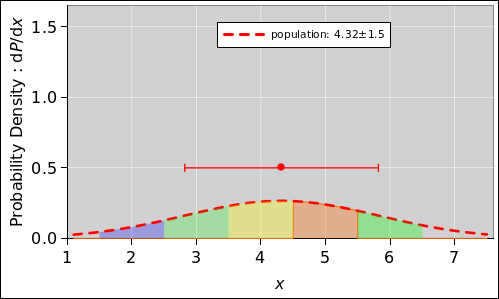
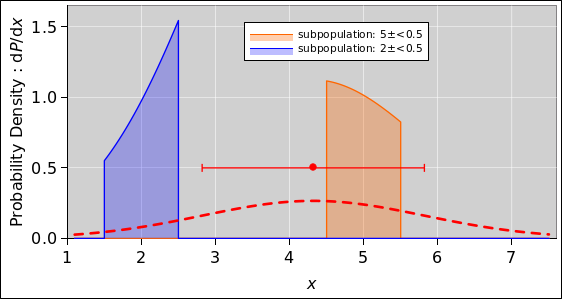
The contrast between figure 4 and figure 5
offers another good way of looking at the same fundamental issue. In
both figures, the red dashed curve represents the distribution of x
in the underlying population, i.e. in the star cluster as a whole. In
figure 4, the orange-shaded region represents the joint
probability that that x occurs in the population and rounds
off to 5 (rounding to the nearest integer). Similarly, the
blue-shaded region represents the joint probability that that x
occurs in the population and rounds off to 2. This is a small,
not-very-probable region.
Meanwhile, in figure 5, the orange-shaded region
represents the conditional probability of finding x in the
population, conditioned on x rounding off to 5. Roughly speaking,
this corresponds to the uncertainty on the position of a single star,
after it has been picked and measured. In a well-designed experiment,
this has almost nothing to do with the width of the distribution as a
whole (i.e. the population as a whole). Similarly, the blue-shaded
region represents the conditional probability of finding x in
the population, conditioned on x rounding off to 2. In this figure,
the area under the blue curve and orange curve are normalized to
unity, as is appropriate for conditional probabilities. The area
under the red curve is also normalized to unity. The sum of the
joint probabilities, summed over all colors, is normalized.
These are all perfectly good distributions, just not the same
distribution. This often leads to confusion at the most basic
conceptual level, because the language is ambiguous: When somebody
says “the error bars on x are such-and-such” it is not the least
bit obvious whether they are talking about the unconditional
distribution (i.e. the underlying population, i.e. the star cluster as
a whole), or about the conditional distribution (i.e. the precision
of a single measurement, after a particular star has been picked and
measured).
To summarize, when you write “5” in the lab notebook there are at
least three concepts to consider.
- The indicated value is xi = 5, with no uncertainty
whatsoever.
- This corresponds to some range of true values, {xt | xi=5}
as represented by the orange-shaded region in figure 5.
This is often a very peculiar distribution, not a normal Gaussian.
However, in a well-designed experiment the details don’t matter much,
provided the distribution has a “small enough” width.
- There is also the unconditional range of true values {x}, as
represented by the red dashed curve in the figures. This is often an
important thing to measure. It usually requires obtaining a great
many xi values and then applying statistical formulas.
There is yet more ambiguity because you don’t know how much the error
bars contribute to the bias as opposed to the variance. For example,
if you round π to 3.14, it contributes precisely nothing to the
variance, because every time you do that the roundoff error is the
same. It does however introduce a bias into the calculation.
Beware: The fact that the conditional probability has some
nonzero width is often used as a pretext for teaching about «sig
figs», even though in a well-designed experiment it is irrelevant.
In any case, it is not recommended to describe uncertainty in
terms of “random numbers” or “uncertain quantities”. As John von
Neumann and others have pointed out, there is no such thing.
There is no such thing as a random number.
If it’s a number, it’s not random.
If it’s random, it’s not a number.
|
|
|
|
People do commonly speak in terms of “random numbers” or “uncertain
quantities”, but that doesn’t make it right. These must be
considered idiomatic expressions and misnomers. See section 4.3 and section 5.2 for more on this.
If you have a random distribution over numbers,
the randomness is in the distribution,
not in any particular number
that may have been drawn from such a distribution.
|
|
|
|
An ultra-simple notion of distribution is presented in
section 2.2. A more robust but still intuitive and
informal introduction to the idea of probability distributions and
probability measures can be found in section 4.3 and
section 5.2. If you want a cheap and easy experiment that
generates data with a nontrivial distribution, partly random and
partly not, consider tack-tossing, as discussed in reference 4. Some tack-tossing data is presented in
figure 6 and figure 7.
For a more formal, systematic discussion of how to think about
probability, see reference 2.
You need to understand the distinction between a number and a
distribution before you do anything with uncertainty. Otherwise
you’re just pushing around symbols without understanding what they
mean.
|
|
|
|
Figure 6: Binomial Distribution : Diaspogram
|
|
Figure 7: Binomial Distribution : XY Scatter Plot
|
|
|
|
|
4 The Importance of Uncertainty
4.1 Sometimes It’s Unimportant or Nonexistent
Sometimes there is uncertainty, but it is unimportant, as mentioned in
section 2.1 and especially section 5.1.
Moreover, sometimes there is no uncertainty, and it would be quite
wrong to pretend there is, especially when dealing with raw data or
when dealing with a particular data point drawn from a distribution,
as discussed in section 5.2.
4.2 Separate versus Bundled Parameters
Suppose we have a distribution over x – perhaps the distribution
shown in figure 1 – and the distribution is
described by a couple of parameters, the mean A and and the standard
deviation B. Consider the contrast:
|
Separate {A, B}
|
|
Bundled A±B
|
|
Sometimes it is best to think of the mean and standard
deviation as two separate, independent parameters.
|
|
Sometimes you
might choose to think of the mean as the “nominal” value of x and
the standard deviation as the “uncertainty” on x.
|
|
This is more abstract and more formal. It is hard to go
wrong with this. One case where it is particularly advantageous is
diffusion, where the mean velocity is expected to be zero, and all you
care about is the RMS velocity.
|
|
This is less formal and more
intuitive. It is advantageous when the average is the primary object
of attention.
|
4.3 Raw Data Points versus Cooked Data Blobs
We must distinguish between raw data points and cooked data
blobs. These are different, as surely as a scalar is different from
a high-dimensional vector. As an example of what I’m talking about,
consider the following contrast:
|
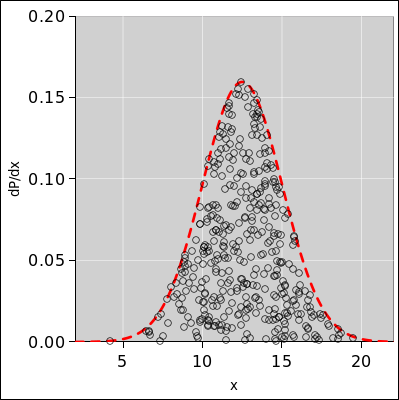
Figure 8 shows 400 data points,
each of which has zero size. The plotting symbols have nonzero size,
so you can see them, but the data itself is a zero-sized point in the
middle of the circle. The distribution over points has some
width. The distribution is represented by the dashed red line.
|
|
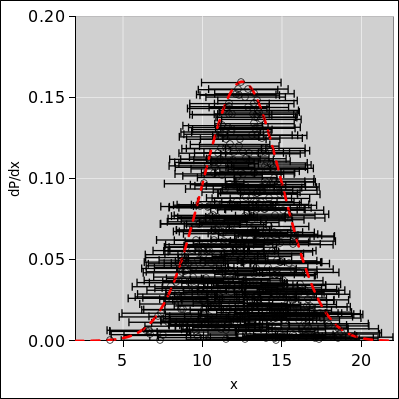
In
figure 9 each data point is shown with
error bars, which is a bad idea. It is (at best) begging to be
interpreted wrongly. It accounts for the same uncertainty twice: Once
by the scatter in the position of the zero-sized points, and again
by the bogus bars attached to the points. Remember, the width is
associated with the distribution, not with any particular raw data
point.
|
|
|
|
|
Figure 8: Samples Drawn from a Gaussian
|
|
Figure 9: Samples with Misbegotten Error Bars
|
|
|
|
|
See also section 5.2. These two figures, and the
associated ideas, are discussed in more detail in reference 2.
Suppose on Monday we roll a pair of slightly-lopsided dice 400 times,
and observe the number of spots each time. Let xi represent the
number of spots on the ith observation. This is the raw data: 400
raw data points. It must be emphasized that each of these raw data
points has no error bars and no uncertainty. The number
of spots is what it is, period. The points are zero-sized pointlike
points.
On Tuesday we have the option of histogramming the data as a
function of x and calculating the mean (A) and standard deviation
(B) of the distribution.
|
For some purposes, keeping track of A±B is more
convenient than keeping track of all 400 raw data points.
|
|
For some
other purposes, A±B does not tell us what we need to know.
|
|
For example, if we are getting paid according to the total
number of spots, then we have good reason to be interested in A
directly and B almost as directly.
|
|
For example, suppose we are using
the dice as input to a random-number generator. We need to know the
entropy of the distribution. It is possible to construct two
distributions with the same mean and standard deviation, but wildly
different entropy. Because the dice are lopsided, we cannot reliably
determine the entropy from A and B alone.
|
|
|
|
As another example: Suppose we are getting paid whenever
snake-eyes comes up, and not otherwise. Because the dice are
lopsided, A and B do not tell us what we need to know.
|
Using the raw data to find values for A and B can be considered an
example of curve fitting. (See section 7.24 for
more about curve fitting.) It is also an example of modeling.
We are fitting the data to a model and determining the parameters of
the model. (For ideal dice, the model would be a triangular
distribution, but for lopsided dice it could be much messier. Beware
that using the measured standard deviation of the set of raw data
points is not the best way to determine the shape or even the
width of the model distribution. This is obvious when there is only a
small number of raw data points. See section 11.4 and
reference 2 for details on this.)
If we bundle A and B together (as defined in section 4.2),
we can consider A±B as a single object, called a blob, i.e. a
cooked data blob. We have the option of trading in 400 raw data
points for one cooked data blob. This cooked data blob represents a
model distribution, which is in turn represented by two numbers,
namely the mean and the standard deviation.
So, this is one answer to the question of why uncertainty is
important: It is sometimes more convenient to carry around one cooked
data blob, rather than hundreds, thousands, or millions of raw data
points. Cooking the data causes a considerable loss of information,
but there is sometimes a valuable gain in convenience.
Note that if somebody gives you a cooked data blob, you can –
approximately – uncook it using Monte Carlo, thereby returning to a
representation where the distribution is represented by a cloud of
zero-sized points. That is, you can create a set of artificial raw
data points, randomly distributed according to the distribution
described by the cooked data blob.
|
In the early stages of data analysis, one deals with raw
data. None of the raw data points has any uncertainty associated with
it. The raw data is what it is. The raw data speaks for itself.
|
|
In
the later stages of data analysis, one deals with a lot of cooked
data. In the simplest case, each cooked data blob has a nominal
value and an uncertainty.
|
|
|
|
If one variable is correlated with some other variable(s),
we have to keep track of all the means, all the standard deviations,
and all the correlations. Any attempt to keep track of separate
blobs of the form A±B is doomed to fail.
|
|
The raw data speaks for
itself.
|
|
|
|
|
|
See section 7.7 for a simple example of a calculation
involving cooked data, showing what can go wrong when there are
correlations. See section 7.15 and section 7.16
for a more elaborate discussion, including one approach to handling
correlated cooked data.
|
Here’s a story that illustrates an important conceptual point:
Suppose we are using a voltmeter. The manufacturer (or the
calibration lab) has provided a calibration certificate that says
anything we measure using this voltmeter will be uncertain
plus-or-minus blah-blah percent. In effect, they are telling us that
there is an ensemble of voltmeters, and there is some spread to the
distribution of calibration coefficients.
Note that any uncertainty associated with the ensemble of voltmeters
is not associated with any of the raw data points. This should be
obvious from the fact that the ensemble of voltmeters existed
before we made any observations. This ensemble is owned by the
manufacturer or the calibration lab, and we don’t get to see more than
one or two elements of the ensemble. So we rely on the calibration
certificate, which contains a cooked data blob describing the
whole ensemble of voltmeters.
Now suppose we make a few measurements. This is the raw data. It
must be emphasized that each of these raw data points has no
error bars and no uncertainty. The data is what it is, period.
At the next step, we can use the raw data plus other information
including the calibration certificate to construct a model
distribution. The ensemble of voltmeters has a certain width. It
would be a tremendous mistake to attribute this width to each of the
raw data points, especially considering that the calibration
coefficient is likely to be very strongly correlated across all of our
raw data.
See section 13.6 for more on this.
4.4 Weighing the Evidence
When dealing with a cooked data blob, it is sometimes very important
to keep track of the width of the blob, i.e. the uncertainty. Far and
away the most common reason for this has to do with weighing the
evidence. If you are called upon to make a judgment based on a
collection of evidence, the task is straightforward if all of the
evidence is equally reliable. On the other hand, if some of the
evidence is more uncertain than the rest, you really need to know how
uncertain it is.
Here’s a non-numerical example: Suppose you are on a jury. there are
ten witnesses who didn’t see what happened, and one who did. It
should go without saying that you really, really ought to give less
weight to the uncertain witnesses.
Now let’s do a detailed numerical example. Suppose we are trying to
diagnose and treat a patient who has some weird symptoms. We have run
11 lab tests, 10 of which are consistent and suggest we should try
treatment “A” while the 11th test suggests we should try treatment
“B”.
In the first scenario, all 11 observations have the same uncertainty.
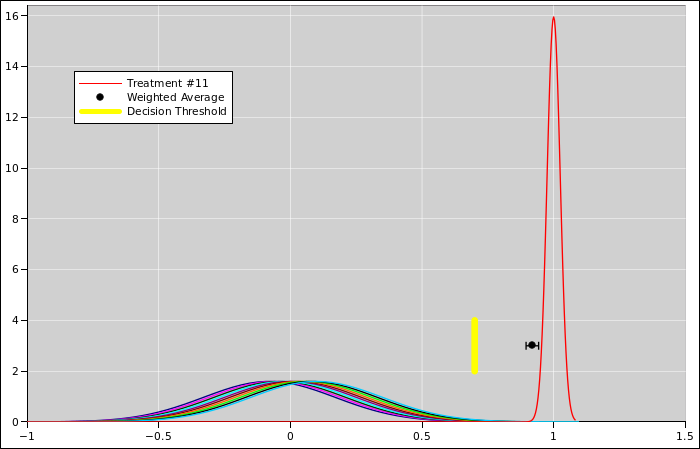
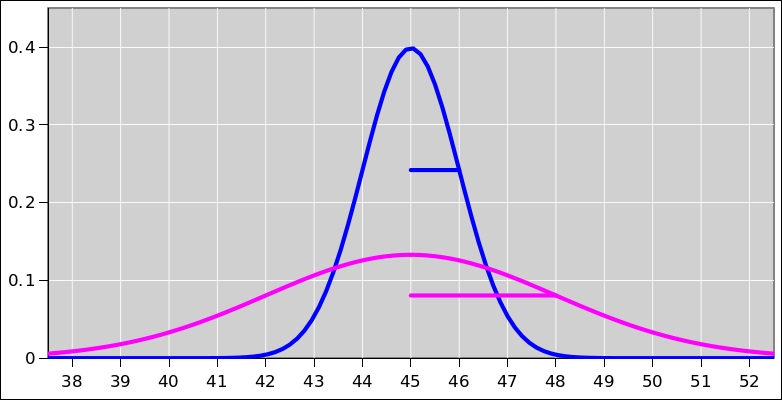
This situation is depicted in figure 10. Each of the
observations is shown as a Gaussian (bell-shaped curve) such that
the width of the curve represents the uncertainty.
In a situation like this, where the observations are equally weighted,
it makes sense to average them. The average x-value is shown by the
black dot, and the uncertainty associated with the average value is
shown by the error bars sticking out from the sides of the dot. We
could have represented this by another Gaussian curve, but for clarity
we represented it as a dot with error bars, which is another way of
representing a probabilistic distribution of observations.
We see that the average is about x=0.1, which is slightly to the
right of x=0. The outlier (the 11th observation) has pulled the
average to the right somewhat, but only somewhat. The outlier is
largely outvoted by the other 10 observations.
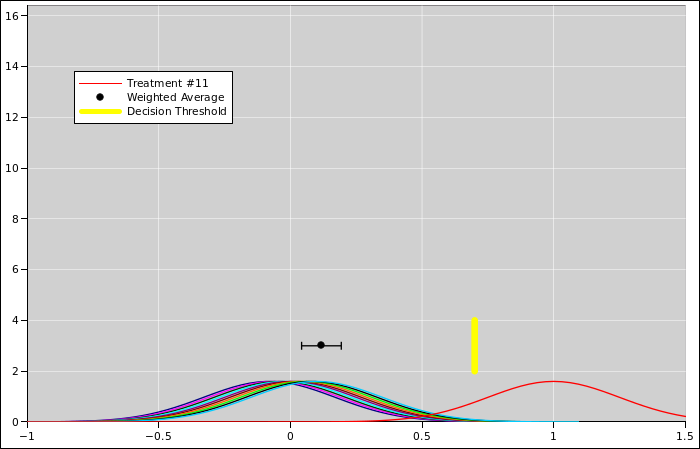
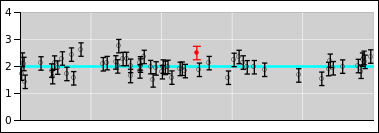
Scenario #2 is the same as scenario #1 except for one detail: The
11th observation was obtained using a technique that has much less
uncertainty. This situation is shown in figure 11.
(We know the 11th curve must be taller because it is narrower, and we
want the area under each of the curves to be the same. For all these
curves, the area corresponds to the total probability of the
measurement producing some value, which must be 100%.)
When we consider the evidence, we must give each observation the
appropriate weight. The observation with the small uncertainty
is given greater weight. When we take the appropriately-weighted
average, it gives us x=0.91. This is represented by the black dot
in figure 11. Once again the uncertainty in the
average is represented by error bars sticking out from the black dot.
It should be obvious that the weighted average
(figure 11) is very, very different from from the
unweighted average (figure 10).
In particular, suppose the yellow bar in the diagram represents the
decision threshold. With unweighted data, the weight of the evidence
is to the left of the threshold, and we should try treatment “A”.
With weighted data, the weight of the evidence is to the right of the
threshold, and we should try treatment “B”.
On the third hand, when considering these 11
observations collectively, it could be argued that the chi-square
is so bad that we ought to consider the possibility that all 11
are wrong, but let’s not get into that right now. Properly
weighing the evidence would be just as important, just slightly
harder to visualize, if the chi-square were lower.
This could be a life-or-death decision, so it is important to know the
uncertainty, so that we can properly weigh the evidence.
4.5 Significant Figures, or Not
The “significant figures” approach is intrinsically and incurably
unable to represent uncertainty to better than the nearest order of
magnitude; see section 8.6 for more on this.
What’s worse, the way that sig figs are used in practice is even
more out-of-control than that; see section 17.5.1 for details.
Everyone who reports results with uncertainties needs to walk
a little ways in the other guy’s moccasins, namely the guy
downstream, the guy who will receive those results and do
something with them.
If the uncertainty is only reported to the nearest order of
magnitude, it makes it impossible for the downstream guy to
collect data from disparate sources and weigh the evidence.
To say the same thing the other way, it is OK to use sig figs
if you are sure that nobody downstream from you will ever use
your data in an intelligent way, i.e. will never want to
weigh the evidence.
Tangential remark: Just to rub salt into the wound: In
addition to doing a lousy job of representing the uncertainty
ΔX, the sig-figs rules also do a lousy job of representing
the nominal value ⟨X⟩ because they introduce
excessive roundoff error. However that is not the topic of this
section.
5 Fundamental Notions of Uncertainty
5.1 Some Things are Certain, and Some are Uncertain
Some things are, for all practical purposes, completely certain. For
example:
- Recently I bought a carton of eggs, and counted how many
eggs it contained. The answer was 12. That means 12, exactly, with
no uncertainty. I am quite certain that there were 12±0 eggs in
that carton. That’s my story, and I’m sticking with it.
- Similarly, I don’t know everything there is to know about the moon,
and I don’t know everything there is to know about cheese, but I am
certain for all practical purposes that the moon is not made of green
cheese.
On the other hand, there is a very wide class of processes that lead
to a distribution of possible outcomes, and these are the main
focus of today’s discussion. Some introductory examples are discussed
in section 5.2.
5.2 Uncertainty ≡ Probability Distribution
The only way to really understand uncertainty is in terms of
probability distributions. You learned in grade-school how to
add, subtract, multiply, and divide numbers ... but in order to deal
with uncertainties you will have to add, subtract, multiply and divide
probability distributions. This requires a tremendously higher level
of sophistication.
An expression such as 45±1 may seem
to represent a number, but it doesn’t.
It represents some kind of probability distribution.
|
|
|
|
If you want a definition of probability, in fundamental and formal
terms, please see reference 2. For the present
purposes we can get along without that, using instead some simple
intuitive notions of probability, as set forth in the following
examples.
As a first example, suppose we roll an ordinary six-sided die and
observe the outcome. The first time we do the experiment, we observe
six spots, which we denote by x1=6. The second time, we observe
three spots, which we denote by x2=3. It must be emphasized that
each of these observations has no uncertainty whatsoever. The
observation x1 is equal to 6, and that’s all there is to it.
If we repeat the experiment many times, ideally we get the probability
distribution X shown in figure 12. To describe the distribution
X, we need to say three things: the outline of the distribution is
rectangular, the distribution is centered at x=3.5, and the
distribution has a half-width at half-maximum (HWHM) of 2.5 units (as
shown by the red bar).
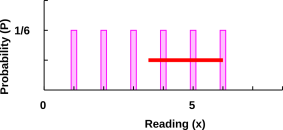 Figure 12
Figure 12: Probability Distribution for a Six-Sided Die
The conventional but abusive notation for describing such a situation
is to write x=3.5±2.5, where x is called a «random variable»
or an «uncertain quantity». I do not recommend this notation or
this way of thinking about things. However, it is sometimes
encountered, so we need a way of translating it into something that
makes more sense.
An expression of the form 3.5±2.5 is a fine way to describe the
distribution X. So far so good. There are however problems with
the x that we encounter in expressions such as x = 3.5±2.5. In
this narrow context evidently x is being used to represent the
distribution X, while in other contexts the same symbol x is used
to represent an outcome drawn from X, or perhaps some sort of
abstract “average” outcome, or who-knows-what. This is an example
of form not following function. Remember, there is a profound
distinction between a number and some distribution from which that
number might have been randomly drawn. See
section 6.4 for more on this.
When you see the symbol x, it is important to appreciate the
distinction between x=3.5±2.5 (which is abusive shorthand for the
distribution X) and particular outcomes such as x1=6 and x2=3
(which are plain old numbers, not distributions):
|
The so-called random variable x “looks” like it might be
one of the observations xi, but it is not. The expression
x=3.5±2.5 does not represent a number; instead it is a shorthand
way of describing the distribution X from which outcomes such
as x1 and x2 are drawn.
|
|
An outcome such as x1 or x2 is
not an uncertain quantity; it’s just a number. In our example, x1
has the value x1=6 with no uncertainty whatsoever.
|
Now suppose we roll two dice, not just one. The first time we do the
experiment, we observe 8 spots total, which we denote by x1=8. The
second time, we observe 11 spots, which we denote by x2=11. If we
repeat the experiment many times, ideally we get the probability
distribution X shown in figure 13. To describe the
distribution X, we need to say that the outline of the distribution
is symmetrical and triangular, the distribution peaks at x=7, and
the distribution has a half-width at half-maximum (HWHM) of 3 units
(as shown by the red bar).
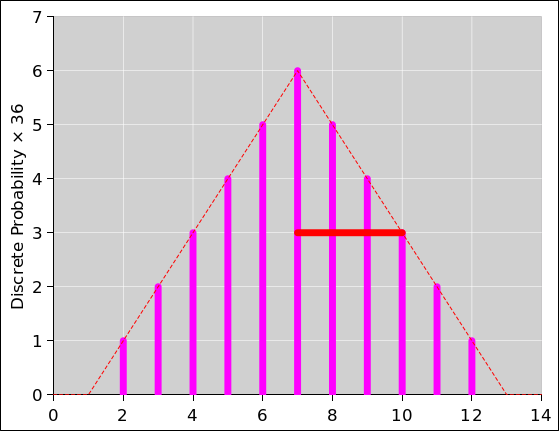 Figure 13
Figure 13: Probability Distribution for a Pair of Dice
Next suppose the outcomes are not restricted to being integers.
Let one of the outcomes be x3=25.37. Once again, these
outcomes are drawn from some distribution X.
We can round off each of the original data points xi and thereby
create some rounded data, yi. For example, x3=25.37 and
y3=25.4. We can also calculate the roundoff error qi := yi −
xi. In our example, we have q3=0.03. Given a large number of
such data points, we can calculate statistical properties such as the
RMS roundoff error. Each xi is drawn from the distribution X,
while each yi is drawn from some different distribution Y, and
each qi is drawn from some even-more-different distribution Q.
The uncertainty is in the distribution,
not in any particular point drawn from the distribution.
|
|
|
|
Consider the probability distribution represented by the colored bands
in figure 14. There is a distribution over
y-values, centered at y=2. Green represents ±1σ from the
centerline, yellow represents ±2σ, and magenta represents
±3σ. The distribution exists as an abstraction, as a thing
unto itself. The distribution exists whether or not we draw any
points from it.
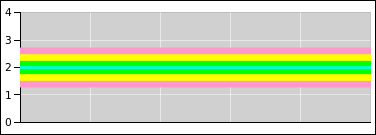 Figure 14
Figure 14: The Distribution Exists Unto Itself
Meanwhile in figure 15, the small circles
represent data points drawn from the specified distribution. The
distribution is independent of x, and the x-coordinate has no
meaning. The points are spread out in the x-direction just to make
them easier to see. The point here is that randomness is a property
of the distribution, not of any particular point drawn from the
distribution.
According to the frequentist definition of probability, if we had an
infinite number of points, we could use the points to define what we
mean by probability ... but we have neither the need nor the desire to
do that. We already know the distribution. Figure 14 serves quite nicely to to define the
distribution of interest.
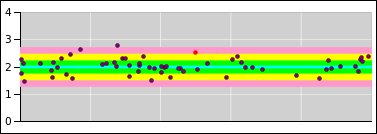 Figure 15
Figure 15: Randomness = Property of the Distribution
By way of contrast, it is very common practice – but not recommended
– to focus attention on the midline of the distribution, and then
pretend that all the uncertainty is attached to the data points, as
suggested by the error bars in figure 16.
In particular, consider the red point in these figures, and consider
the contrasting interpretations suggested by
figure 15 and
figure 16.
|
Figure 15 does a good job of
representing what’s really going on. It tells us that the red point
is drawn from the specified distribution. The distribution has a
standard deviation of σ=0.25 and is centered at y=2 (even
though the red dot is sitting at y=2.5).
|
|
Figure 16 incorrectly suggests that the red point
represents a probability distribution unto itself, allegedly centered
at y=2.5 and extending symmetrically above and below there, with an
alleged standard deviation of σ=0.25.
|
|
Specifically, the red point sits approximately 2σ
from the center of the relevant distribution as depicted in
figure 15. If we were to go up another
σ from there, we would be 3σ from the center of the
distribution.
|
|
Figure 16 wrongly
suggests that the top end of the red error bar is only 1σ from
the center of “the” distribution i.e. the alleged red distribution
... when in fact it is 3σ from the center of the relevant
distribution. This is a big deal, given that 3σ deviations are
quite rare.
|
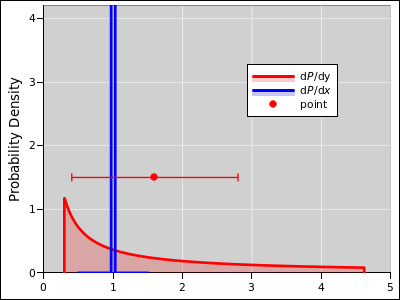
Things get more interesting when the model says the uncertainty varies
from place to place, as in figure 17. The
mid-line of the band is a power law, y = x3.5. The uncertainty
has two components: an absolute uncertainty of 0.075, “plus” a
relative uncertainty of 0.3 times the y-value. The total
uncertainty is found by adding these two components in quadrature.
This sort of thing is fairly common. For instance, a the calibration
certificate for a voltmeter might say the uncertainty is such-and-such
percent of the reading plus this-or-that percent of full scale.
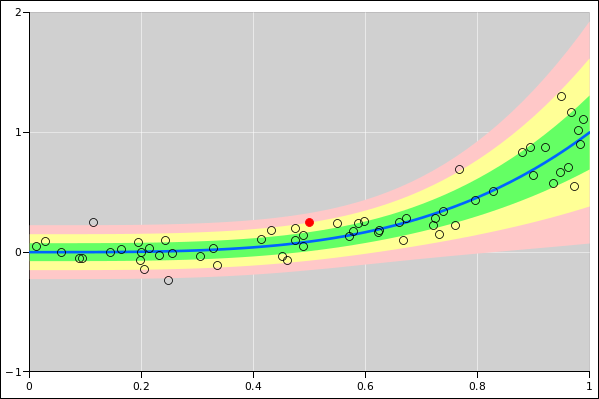 Figure 17
Figure 17: Band Plot: Absolute plus Relative Error
Note that on the left side of the diagram, the total uncertainty –
the width of the band – is dominated by the absolute uncertainty,
whereas on the right side of the diagram, the total uncertainty is
dominated by the relative uncertainty.
Figure 18 shows the same data, plotted
on log/log axes. Note that log/log axes are very helpful for
visualizing some aspects of the data, such as the fact that the power
law is a straight line in this space. However, log/log axes can also
get you into a lot of trouble. One source of trouble is the fact that
the error bands in figure 17 extend into
negative-y territory. If you take the log of negative number, bad
things are going to happen.
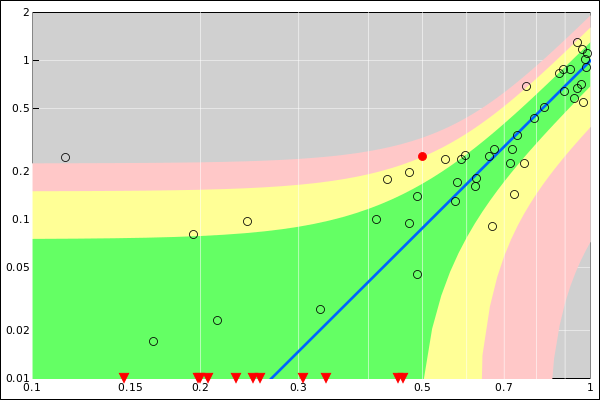 Figure 18
Figure 18: Band Plot: Absolute plus Relative Error; Log/Log Axes
In figure 18, the red downward-pointing
triangles hugging the bottom edge of the triangle correspond to
off-scale points. The abscissa is correct, but the ordinate of such
points is unplottable.
The spreadsheet used to create this figures is given in reference 5.
Band plots (as in figure 15 or figure 17) are extremely useful. The technique is not
nearly as well known as it should be. As a related point, it is
extremely unfortunate that the commonly-available plotting tools do
not support this technique in any reasonable way.
Tangential remark: This can
be seen as reason #437 why sig figs are a bad idea. In this
case, sig figs force you to attribute error bars to every data
point you write down, even though that’s conceptually wrong.
Please see reference 2 for a discussion of
fundamental notions of probability, including
- The idea that a distribution has width but a point does not.
- Probability density distributions versus cumulative probability
distributions.
- Distributions over a continuous variable verus distributions
over a discrete variable.
5.3 Analog Measurements
There are lots of analog measurements in the world. For
example:
- Every time you draw a scale diagram of the apparatus or draw a graph
you are in effect recording some measurements in analog form.
- If you are in the field, and you brought your notebook but not
your ruler, it might be perfectly sensible to write down that one
beetle was
|―――|
long while another was
|――――|
long.
- Et cetera.
Analog measurements are perfectly reasonable. There are ways of
indicating the uncertainty of an analog measurement. However, these
topics are beyond the scope of the present discussion, and we shall
have nothing more to say about them.
5.4 Digital Measurements
Here are the main cases and sub-cases of interest:
-
Sometimes we make a digital measurement of something that is
intrinsically digital and discrete, such as the number of beans in a
jar, or the number of photons received by a photon counter.
- Sometimes we make a digital measurement of something that started out
as a continuous, analog signal (such as time, distance, voltage, etc.)
but was subsequently digitized.
5.5 Indicated Value versus True Values
It helps to distinguish the indicated value from the true
values. Let’s consider a couple of scenarios:
Scenario A: We hook a digital voltmeter to a nice steady
voltage.
|
We observe that the meter says 1.23 volts. This is the
indicated voltage. It is known.
|
|
There is “some” true voltage at the
input. We will never know the exact voltage, which is OK, because we
don’t need to know it.
|
|
If the meter is broken, the true voltage could be wildly
different from the indicated voltage.
|
|
Since this is a digital instrument, the indicated values are
discrete.
|
|
The true voltage is a continuous variable.
|
In general, each indicated value corresponds to a range of true
values, or some similar distribution over true values. For example,
in the case of an ideal voltmeter, the relationship might follow the
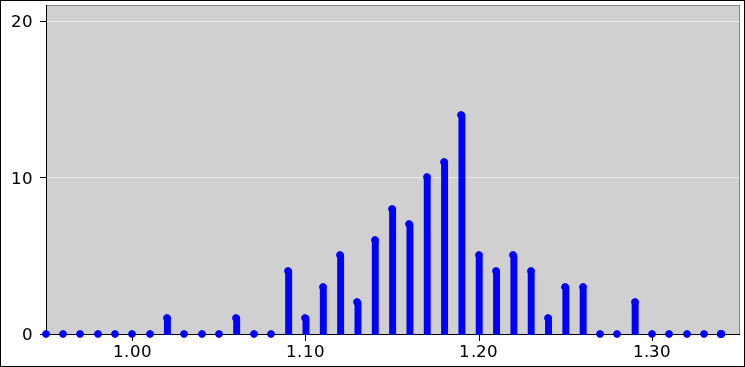
pattern shown in table 1.
| indicated | | range of |
| value | | true values |
| 1.1 | : | [1.05, | 1.15] |
| 1.2 | : | [1.15, | 1.25] |
| 1.3 | : | [1.25, | 1.35] |
| 1.4 | : | [1.35, | 1.45] |
| etc. | | etc.
|
Table 1: Ideal Voltmeter : True Value versus Indicated Value
Scenario B: Using a couple of comparators, we arrange to show a green
light whenever the voltage is greater than −12 volts and less than
+12 volts, and a red light otherwise. That is to say, a “green
light” indication corresponds to a true value in the interval
0±12 volts.
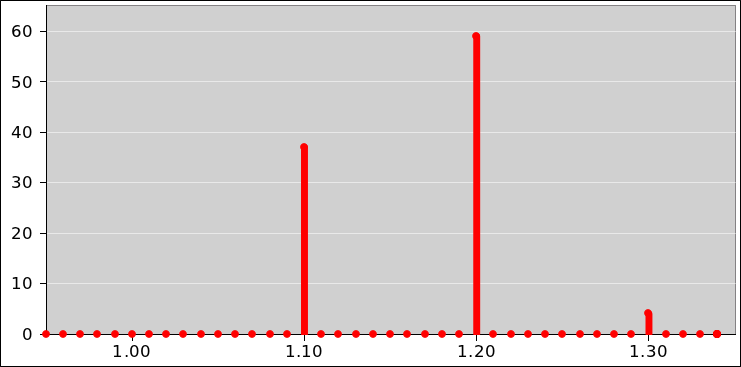
| indicated | | range of |
| value | | true values |
| Green | : | [−12, | 12] |
| Red | : | (−∞, | −12) ∪ (12, | ∞) |
Table 2: Green/Red Voltage Checker : True Value versus Indicated Value
Instruments with non-numerical outputs are quite common in industry,
used for example in connection with “pass/fail” inspections of
incoming or outgoing merchandise. There are many indicators of this
kind on the dashboard of your car, indicating voltage, oil pressure,
et cetera.
|
In both of these scenarios, the indicated value is
discrete.
|
|
The true value is a continuous, analog variable.
|
|
If the indicated value is not fluctuating, it can be
considered exact, with zero uncertainty, with 100% of the
probability.
|
|
The true value will always have some nonzero
uncertainty. It will never be equal to this-or-that number.
|
|
Even if the indicated value is fluctuating, there will be a
finite set of indications that share 100% of the probability. Each
member of the set will have some discrete, nonzero probability.
|
|
No
specific true value occurs with any nonzero probability. The best we
can do is talk about probability density, or about the probability of
true values in this-or-that interval.
|
The indicated value will never be exactly equal to the true value.
This is particularly obvious in scenario B, where the indicated value
is not even numerical, but is instead an abstract symbol.
Still, the indicated value does tell us “something” about the true
value. It corresponds to a range of true values, even
though it cannot possibly equal the true value.
You should not imagine that things will always be as simple as the
examples we have just seen.
- For one thing, in table 1 the true-value
intervals are uniformly spaced and non-overlapping, but this is not
the general case. A counterexample is presented in section 6.1,
where we see nonuniformity and lots of overlap. Also in
section 19 the intervals are nonuniform.
- In table 1 the indicated values correspond to
rounding off the true values, so the true-value intervals can be
“explained” in terms of roundoff error.
- This is clearly not the case in in table 2,
where the interval 0±12 could not possibly have resulted from
rounding off decimal digits (since that always results in ± half a
count in the last decimal place). We also note that this interval
could not possibly be represented by sig figs. Not even close.
- It is also not the case in section 6.1, where the
uncertainty is dominated by calibration issues, not by readability or
roundoff. (You can always make roundoff the dominant issue, but
only by rounding off too much, to the point where your data is
seriously degraded.)
- It is also not the case with the number of centimeters per inch.
Sometimes a decimal such as 2.54 is obtained by rounding off, and
sometimes it isn’t.
- Very commonly, computer audio systems use 256 binary levels
internally, but the user interface expresses things on a scale of 0 to
100%, in steps of 1%, which means that some indicated values
correspond to an interval of two real values, while other readings
correspond to an interval of three real values. So this is
another example of non-uniform intervals.
- Ditto for the RGB color codes in many computer graphic
systems.
- You can’t use “sig figs” ideas to determine the size of the
true-value ranges. I’ve seen instruments that count by twos in the
last decimal place, and others that count by fives in the last decimal
place. In such cases the quantization intervals are much larger than
you might guess just by counting digits in the display.
Terminology: The true-value intervals (such as we see in
table 1) go by various names. In the context of
digital instruments people speak of resolution, quantization error,
and/or roundoff error. In the context of analog instruments they
speak of resolution and/or readability.
In a well-designed experiment, these issues are almost never the
dominant contribution to the overall uncertainty. This leads to
an odd contrast:
|
When designing apparatus and procedures, you absolutely must
understand these issues well enough to make sure they will not cause
problems.
|
|
Later, during the day-to-day operation of a well-designed
procedure, you can almost forget about these issues. Almost. Maybe.
|
5.6 Uncertainty ± Error ≠ Mistake
Keep in mind that we are using the word uncertainty to refer to
the width of a probability distribution ... nothing more, nothing
less.
Sometimes this topic is called “error analysis”, but beware that
the word “error” is very widely misunderstood.
|
In this context, the word “error” should not be considered
pejorative. It comes from a Latin root meaning travel or journey.
The same root shows up in non-pejorative terms including errand and
knight-errant.
|
|
Some people think that an error is Wrong with a
capital W, in the same way that lying and stealing are Wrong,
i.e. sinful. This is absolutely not what error means in this
context.
|
In this context, error means the same thing as uncertainty. It refers
to the width of the distribution, not to a mistake or blunder. Indeed,
we use the concept of uncertainty in order to avoid making
mistakes. It would always be a mistake to say the voltage
was exactly equal to 1.23 volts, but we might be confident
that the voltage was in the interval 1.23±0.05 volts.
The proper meaning of uncertainty (aka “error”) is well illustrated
by Scenario B in section 5.5. The comparator has a wide
distribution of true voltages that correspond to the “green light”
indication. This means we are uncertain about the true voltage. This
uncertainty is, however, not a blunder. Absolutely not. The width of
the distribution is completely intentional. The width was carefully
designed, and serves a useful purpose.
This point is very widely misunderstood. For example, the cover of
Taylor’s book on Error Analysis (reference 6) features a
crashed train at the Gare Montparnasse, 22 October 1895. A train
crash is clearly an example of a shameful mistake, rather than a
careful and sophisticated analysis of the width of a distribution.
It’s a beautiful photograph, but it conveys entirely the wrong idea.
See also section 8.12.
5.7 Probably Almost Correct
Consider the following contrast:
|
I have zero confidence that the value of π is in the
interval [3.14 ± 0.001].
|
|
I have 100% confidence that the value
of π is in the interval [3.14 ± 0.002].
|
|
In this case, we have a tight tolerance but low confidence.
|
|
Using a wider tolerance gives us a vastly greater confidence.
|
|
If you demand exact results, you are going to be bitterly
disappointed. Science rarely provides exact results.
|
|
If you are
willing to accept approximate results within some reasonable tolerance
interval, science can deliver extremely reliable, trustworthy
results.
|
|
Science does not achieve perfection, or even try for
perfection.
|
|
What we want is confidence. Science provides extremely
powerful, high-confidence methods for dealing with an imperfect
world.
|
5.8 Identify All Contributions to the Uncertainty
Accounting for uncertainty is not merely an exercise in mathematics.
Before you can calculate the uncertainty in your results, you need to
identify all the significant sources of uncertainty. This is a major
undertaking, and requires skill and judgment.
For example: The voltmeter could be miscalibrated. There could be
parallax error when reading the ruler. There could be bubbles in the
burette. The burette cannot possibly be a perfectly uniform cylinder.
There could be moisture in the powder you are weighing. And so on and
so on.
Four categories of contributions that are almost always present to
some degree are fluctuations, biases, calibration errors, and resolution
problems aka roundoff errors, as we now discuss.
- Suppose you are looking at a meter and the needle is wiggling all over
the place. It doesn’t matter how well calibrated the meter is or how
finely graduated the scale is. The inherent scatter in the
readings overwhelms other contributions to the uncertainty.
- You can reduce the noise by averaging the signal, but this
introduces a bias, insofar as part of the signal you are supposed to
be measuring will be outside the passband of the filter. In general
there will be noise/bandwidth tradeoffs. Even more generally, there
will be variance/bias tradeoffs.
- Now suppose the signal is not fluctuating, and you can read the
scale very accurately. In such a case, it may be that calibration
errors are the dominant contribution to the uncertainty.
- Suppose you know that a certain landmark is between 32∘ and
33∘ north latitude, at some well-known longitude. There is no
question of fluctuations, since the landmark is not moving. Also
there is no problem with the calibration, since we know where the
lines of latitude are, with an uncertainty of well less than 1 meter.
Yet still we have many kilometers of uncertainty about the location of
the landmark, because our information is too coarsely quantized. We
don’t have enough resolution. In other words, we are getting
clobbered by roundoff errors.
Remark #1: Remember: Roundoff error is only one contribution to the
overall uncertainty. In a well-designed experiment, it is almost
never the dominant contribution. See section 8.6
for a discussion of how distributions are affected by roundoff errors.
Remark #2: It is not safe to assume that roundoff errors are
uncorrelated. It is not safe to assume that calibration errors are
uncorrelated. Beware that many textbooks feature techniques that might
work for uncorrelated errors, but fail miserably in practical
situations where the errors are correlated.
Remark #3: If one of these three contributions is dominant, it is
fairly straightforward to account for it while ignoring the others.
On the other hand, if more than one of these contributions are
non-negligible, the workload goes up significantly. You may want to
redesign the experiment.
If you can’t redesign the experiment, you might still
be able to save the day by finding some fancy way to account for
the various contributions to the uncertainty. This, however, is
going far beyond the scope of this document
Remark #4: More specifically: You usually want to design the
experiment so that the dominant contribution to the uncertainty comes
from the inherent fluctuations and scatter in the variable(s) of
interest. Let’s call this the Good Situation.
It’s hard to explain how to think about this. In the Good Situation,
many idealizations and simplifications are possible. For example:
since calibration errors are negligible and roundoff errors are
negligible, you can more-or-less ignore everything we said in
section 5.5 about the distinction between the indicated
value and the range of true values. If you always live in the Good
Situation, you might be tempted to reduce the number of concepts that
you need to learn. If you do that, though, and then encounter a
Not-So-Good Situation, you are going to be very confused, and you will
suddenly wish you had a better grasp of the fundamentals.
Possibly helpful suggestion: A null experiment – or at least a
differential experiment – often improves the situation twice over,
because (a) it reduces your sensitivity to calibration errors, and (b)
after you have subtracted off the baseline and other common-mode
contributions, you can turn up the gain on the remaining
differential-mode signal, thereby improving the resolution and
readability.
5.9 Empirical Distributions versus Theoretical Distributions
There are many probability distributions in the world, including
experimentally-observed distributions as well as
theoretically-constructed distributions.
Any set of experimental observations {xi} can be considered a
probability distribution unto itself. In simple cases, we assign
equal weight (i.e. equal measure, to use the technical term) to
each of the observations. To visualize such a distribution, often the
first thing to do is look a scatter plot. For example,
figure 34 shows a two-dimensional scatter plot, and
figure 37 shows a one-dimensional scatter plot. We
can also make a graph that shows how often xi falls within a given
interval. Such a graph is called a histogram. Examples
include figure 12, figure 13, and figure 22.
Under favorable conditions, given enough observations, the histogram
may converge to some well-known theoretical probability
distribution. (Or, more likely, the cumulative distribution will
converge, as discussed in reference 2.) For
example, it is very common to encounter a piecewise-flat distribution
as shown by the red curve in figure 19.
This is also known as a square distribution, a rectangular
distribution, or the uniform distribution over a certain interval.
Distributions of this form are common in nature: For instance, if you
take a snapshot of an ideal rotating wheel at some random time, all
angles between 0 and 360 degrees will be equally probable. Similarly,
in a well-shuffled deck of cards, all of the 52-factorial permutations
are equally probable. As another example, ordinary decimal roundoff
errors are confined to the interval [-0.5, 0.5] in the last decimal
place. Sometimes they are uniformly distributed over this interval
and sometimes not. See section 8.3 and
section 7.12 for more on this. Other quantization errors
(such as discrete drops coming from a burette) contribute an
uncertainty that might be more-or-less uniform over some interval
(such as ± half a drop).
It is also very common to encounter a Gaussian distribution (also
sometimes called a “normal” distribution). In figure 19, the blue curve is a Gaussian distribution.
The standard deviation is 1.0, and is depicted by a horizontal green
bar. The standard deviation of the rectangle is also 1.0, and is
depicted by the same green bar.
Meanwhile, the HWHM of the Gaussian is depicted by a blue bar, while
the HWHM of the rectangle is depicted by a red bar.
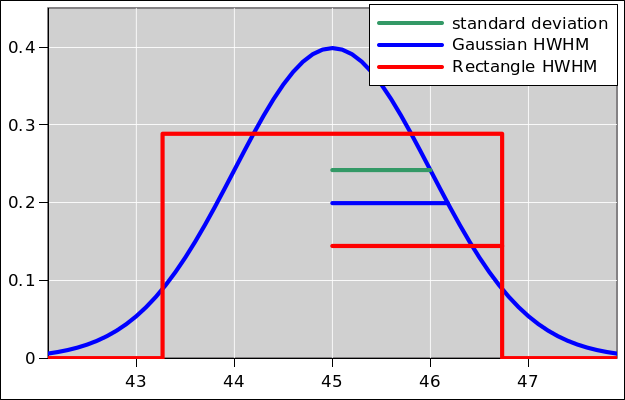 Figure 19
Figure 19: Gaussian vs. Rectangular; StDev vs. HWHM
Table 3 lists a few well-known families of distributions.
See section 13.8 for more on this.
| Family | | # of parameters | | example |
|
| Bernoulli | | 1 | | coin toss |
| Poisson | | 1 | | counting random events |
| Gaussian | | 2 | | white noise |
| Rectangular | | 2 | | one die; also roundoff (sometimes) |
| Symmetric triangular | | 2 | | two dice |
| Asymmetric triangular | | 3
| |
Each of these distributions is discussed in more detail in reference 2.
Each name in table 3 applies to a family of
distributions. Within each such family, to describe a particular
member of the family (i.e. a particular distribution), it suffices to
specify a few parameters. For a symmetrical two-parameter family,
typically one parameter specifies the center-position and the second
parameter has something to do with the halfwidth of the distribution.
The height of the curve is implicitly determined by the width, via the
requirement2 that the area under the
curve is always 1.0.
In particular, when we write A±B, that means A tells us the
nominal value of the distribution and B tells us the
uncertainty or equivalently the error bar. See
section 5.12 for details on the various things we might mean
by nominal value and uncertainty.
5.10 Terminology and Notation
Best current practice is to speak in terms of the uncertainty.
We use uncertainty in a broad sense. Other terms such as accuracy,
precision, experimental error, readability, tolerance, etc. are often
used as nontechnical terms ... but sometimes connote various sub-types
of uncertainty, i.e. various contributions to the overall uncertainty,
as discussed in section 12. In most of this document,
the terms “precise” and “precision” will be used as generic,
not-very-technical antonyms for “uncertain” and “uncertainty”.
As a related point, see section 13.7 for details on why we
avoid the term “experimental error”.
Some guidelines for describing a distribution are given in
section 1.2. When writing the nominal value and the standard
deviation, be sure to write them separately, using two separte
numerals. For example, NIST (reference 7) reports the charge
of the electron as
| 1.602176462(63) × 10−19 coulombs (4) |
which is by definition equivalent to
⎛
⎜
⎝ |
| | ⎞
⎟
⎠ | × 10−19 coulombs
(5) |
Note that this value departs from the usual “sig-digs rules” by
a wide margin. The reported nominal value ends in not one but two
fairly uncertain digits.
For specific recommendations on what you should do, see
section 8.2. Also, NIST offers some prescriptions on how to
analyze and report uncertainties; see reference 8,
reference 9, and reference 10.
Additional discussions of how to do things can be found in
reference 11 and reference 12.
5.11 How Not to Represent Uncertainty
The “significant figures” method attempts to use a single decimal
numeral to express both the center and the halfwidth of a
distribution: the ordinary value of the numeral encodes the center,
while the length of the string of digits roughly encodes the
halfwidth. This is a horribly clumsy way of doing things.
See section 1.3 and section 17.
5.12 Uncertainty, Standard Deviation, Confidence Limits, etc.
In the expression A±B, we call A the nominal value and B the
uncertainty (or, equivalently, the error bar).
We will explicitly avoid giving any quantitative definition for the
terms nominal value and uncertainty. This is because
there is not complete consensus as how to quantify the expression
A±B. When you write such an expression, it is up to you to
specify exactly what you mean by it. When you read such an
expression, you will have to look at the context to figure out what it
means.
- For a mathematically ideal Gaussian distribution, there is a
reasonably strong consensus that in the expression A±B, the
nominal value (A) is the mean. In this case the mean is also the
median and the mode and the center of symmetry, so there is not
really much to debate.
Meanwhile, as for B:
- Conventionally the uncertainty (B) is the standard
deviation, B=σ. The interval from A−σ to A+σ
is the 68% confidence interval.
- In specialized situations, people might be interested in the
interval from from A−2σ to A+2σ, which is the 95%
confidence interval, or even the interval from from A−3σ to
A+3σ, which is the 99.73% confidence interval.
However, if you are going to use two-sigma or three-sigma error
bars, you need to warn people, because this is not what they are
expecting. Normally, for a Gaussian, the expression A±B
communicates the mean plus-or-minus one sigma.
- For a mathematically ideal symmetrical triangular
distribution, again the nominal value A is the mean and the median
and the mode and the center of symmetry.
As for the uncertainty, there are at least two reasonable choices.
B could represent the standard deviation, or it could
represent the HWHM.
- The interval from A−σ to A+σ is the 65%
confidence interval. This has the advantage of using the A±B
symbol the same way for both Gaussian and triangular distributions:
it communicates the mean and standard deviation.
- The interval from A−HWHM to A+HWHM is the 75%
confidence interval. This has the advantage of being a natural
geometrical feature of the triangle.
- For a mathematically ideal rectangular distribution, once
again A conventionally represents the mean and the median and the
center of symmetry. The distribution does not have a peak, properly
speaking, so there is no mode.
Again there are reasonable arguments for using the standard
deviation to quantify the uncertainty, and also reasonable
arguments for using the HWHM. Both are commonly used:
- The interval from A−σ to A+σ is the 58%
confidence interval. This has the advantage of using the A±B
symbol the same way for both Gaussian and rectangular distributions:
it communicates the mean and standard deviation.
- The interval from A−HWHM to A+HWHM is the 100%
confidence interval. This has the advantage of being a natural
geometrical feature of the rectangle. Indeed this is
the raison d’être for the rectangular distribution:
all of the probability lies within ±1 HWHM of the middle.
In all cases the uncertainty B is more closely related to the
halfwidth than to the full width, since the expression A±B is
pronounced A plus-or-minus B, not plus-and-minus. That is to say,
B represents the plus error bar or the minus error bar separately,
not both error bars together.
For a distribution defined by a collection of data, we need to proceed
even more carefully. The data itself has a perfectly well defined
mean and standard deviation, and you could certainly compute the mean
and standard deviation, using the definition directly. These are
called the sample-mean and the sample-standard-deviation. These
quantities are well defined, but not necessarily very useful. Usually
it is smarter to assume that the data is a sample drawn from some
underlying mathematically-defined distribution, – called the
population – and to use the data to estimate the parameters of the
population. The mean of the data might not be the best estimator of
the mean of the population. (When the number of data points is not
very large, the standard deviation of the sample is a rather badly
biased estimator of the standard deviation of the population)
Also, remember: An expression of the form A±B only makes sense
provided everybody knows what family of distributions you are talking
about, provided it is a well-behaved two-parameter family, and
provided everybody knows what convention you are using to quantify the
nominal value and the uncertainty. To say the same thing the other
way: it is horrifically common for people to violate these provisos,
in which case it A±B doesn’t suffice to tell you what you need
to know. For example: in figure 19, both curves
have the same mean and the same standard deviation, but they are
certainly not the same curve. Data that is well described by the blue
curve would not be well described by the red curve, nor vice versa.
6 Reading an Instrument
6.1 Example: Reading a Meter
It is very common to have an analog meter where the calibration
certificate says the uncertainty is 2% of the reading plus 2% of
full scale. The latter number means there is some uncertainty as to
the “zero offset” of the meter.
When dealing with uncertainty, it helps to keep in mind the
distinction between the indicated value and the true value. As
discussed in section 5.5, even when the indicated value
is known with zero uncertainty, it usually represents a range of true
values with some conspicuously non-zero uncertainty.
This tells us that when the indicated value is at the top of the
scale, the distribution of of true values has a relative uncertainty
of 3 or 4 percent (depending on whether you think the various
contributions are independent). More generally, the situation is
shown in table 4.
| indicated | | range of | absolute | relative |
| value | | true values | uncertainty | uncertainty |
| 0 | : | [-0.02, | 0.02] | | 0.02 | ∞ |
| 0.05 | : | [0.03, | 0.07] | | 0.02 | 40.05% |
| 0.1 | : | [0.08, | 0.12] | | 0.0201 | 20.1% |
| 0.2 | : | [0.18, | 0.22] | | 0.0204 | 10.2% |
| 0.3 | : | [0.28, | 0.32] | | 0.0209 | 6.96% |
| 0.4 | : | [0.38, | 0.42] | | 0.0215 | 5.39% |
| 0.5 | : | [0.48, | 0.52] | | 0.0224 | 4.47% |
| 0.6 | : | [0.58, | 0.62] | | 0.0233 | 3.89% |
| 0.7 | : | [0.68, | 0.72] | | 0.0244 | 3.49% |
| 0.8 | : | [0.77, | 0.83] | | 0.0256 | 3.2% |
| 0.9 | : | [0.87, | 0.93] | | 0.0269 | 2.99% |
| 1 | : | [0.97, | 1.03] | | 0.0283 | 2.83% |
As you can see in the table, as the readings get closer to the bottom
of the scale, the absolute uncertainty goes down, but the relative
uncertainty goes up dramatically. Indeed, if the reading is in the
bottom part of the scale, you should switch ranges if you can ... but
for the moment, let’s suppose you can’t.
Keep in mind that calibration errors are only one of many
contributions to the overall uncertainty.
Let’s turn now to another contribution, namely readability.
Imagine that the meter is readable to ±2% of full scale. That
means it is convenient to express each reading as a two-digit number.
You should record both digits, even in the bottom quarter of the
range, where the associated uncertainty is so large that the sig figs
rules would require you to round off. You should record both digits
because:
- Recording both digits is easier than worrying about whether both
digits are necessary.
- Rounding off is error-prone and should not be done on the fly.
- Rounding off introduces roundoff error and you don’t
want to do that if there’s no need to.
- Even in the best of circumstances, the sig figs method gives
only a very crude estimate of the uncertainty. If at some point you
switch from two digits to one digit, it would imply that the
uncertainty suddenly went up by a factor of ten. It’s silly
to do that, given that we have much better information
about the uncertainty. We know that it is 2% of the reading
plus 2% of full scale.
You should write a note in the lab book saying
what you know about the situation:
Calibration good to 2% of reading plus 2% of full scale.
Scale readable to 2%.
Then just record each indicated value, as is. Two decimal places
suffice to guarantee that the roundoff error is not larger than the
readability interval. Remember that the indicated value is known with
zero uncertainty, but represents a distribution of true values.
Writing such a note in the lab book, and then writing the indicated
values as plain numbers, is incomparably easier and better than
trying to describe the range of true values for every observation on a
line-by-line basis.
This upholds the important rule: say what you mean, and mean what you
say. Describing the calibration and readability situation and then
writing down the indicated values makes sense, because you are writing
down what you know, nothing more and nothing less.
Also note that this upholds the rule of specifying the uncertainty
separately, rather than trying to encode it using sig figs. You
should never try to use one numeral to represent two numbers.
6.2 Example: Reading a Burette using Simple Interpolation
Figure 20 is a photograph3 of some liquid in a burette.
For present purposes, this photograph is our raw data. Our task is to
read the data, so as to arrive at a numerical reading.
Let’s start by taking the simple approach. (See
section 6.3 for a fancier approach.
To get a decent accuracy, we divide the smallest graduation in
half. Therefore readings will be quantized in steps of 0.05 mL.
More to the point, that gives us a readability of ±0.025
mL, since the indicated value will differ from the true value by at
most half a step in either direction.
Using this approach, I observe that the meniscus is pretty close to
the 39.7 graduation. It is not halfway to 39.8, or even halfway to
halfway, so it is clearly closer to 39.7 than to 39.75. Therefore I
would record the indicated value as 39.7 mL (with a readability of
±0.0125 mL.
6.3 Example: Reading a Burette using Fancy Interpolation
We now start over and re-do the interpolation. We work a lot harder
this time, so as to obtain a more accurate result.
It is not always worthwhile to go to this much trouble,
but sometimes it is.
- Take a picture using a digital camera. Note that in
figure 20, the camera has been carefully lined up so
as to minimize parallax errors. Also the lighting has been arranged
so that the meniscus shows up clearly.
- Read the picture into a graphics program such as inkscape.
- Magnify it 500% so that squinting is not necessary, as shown in
figure 21.
- Look closely at the picture. In this example, you see the
following, in order from top to bottom: Background; liquid (darker
than the background); lower boundary of the liquid (very dark);
bright halo (brighter than the background); background again.
I choose to define “the” position of the meniscus as the boundary
between the dark boundary and the bright halo. Others may choose
differently. The choice doesn’t matter much for typical chem-lab
purposes (so long as the choice is applied consistently), because
when using a burette we are almost always interested in the
difference between two readings.
- Fit the boundary of the meniscus to the boundary of a drawn
object, such as the red object shown in
figure 21. Note that the red object has a
partially-transparent interior. This allows you to slide it around
and still see what’s behind it. Also note that it has no boundary
line. This makes use of a profound mathematical fact: the boundary
of a boundary is zero. That is to say, the boundary of the red
object has zero width, whereas if you drew a line, you would need to
worry about the width of the line.
It is not hard to position the boundary of the red object against the
boundary of the liquid with sub-pixel accuracy. It may help to
reduce the opacity of the red object during this step.
- Add additional graduations, as shown by the thin cyan lines in
figure 21. Up to a point, counting
closely-spaced lines is easier than interpolating between
widely-spaced lines ... and interpolation over short distances is
easier than interpolation over long distances.
- Read out the position of the boundary of the red object. Forget
about the raw-data pixels at this point, because they are blurry
while the red object is not. It may help to increase the opacity of
the red object during this step.
Following this procedure, I decide the indicated value is 39.71,
readable to the nearest .01 mL. That is to say, the readability is
±0.005 ml. Note that this approach gives us five times better
accuracy, compared to the simple approach in
section 6.2.
It is not be necessary to computer-analyze every burette reading. For
one thing, in many cases you don’t need to know the reading to this
degree of accuracy. Secondly, with a little bit of practice you can
read this burette by eye to the nearest 0.01 mL, without the aid of
the computer. A detailed analysis is worth the trouble every once in
a while, if only to increase your eyeball skills, and to give you
confidence in those skills. Interpolating by eye to one tenth of a
division is doable, but it is not easy. Nobody was born knowing how
to do this.
At some point readability gets mixed up with quantization error aka
roundoff error associated with the numbers you write down. In this
example, I have chosen to quantize the reading in steps of 0.01 ml.
This introduces a roundoff error of ± 0.005 ml ... with a very
non-Gaussian distribution.
Remember: In a well-designed experiment, roundoff error is almost
never the dominant contribution to the overall uncertainty. In this
case, the roundoff error is less than the uncertainty due to my
limited ability to see where the meniscus actually is, so I’m
not going to worry too much about it.
It is hard to know the readability for sure without repeating the
measurement N times and doing some sort of statistical analysis.
For reasons discussed in section 6.1 and section 6.4, you probably do not want to record this in the
form 39.71 ± 0.005, because people will interpret that as a
statement of “the” uncertainty, whereas readability is only one
contribution to the overall uncertainty. It is better to simply make
a note in the lab book, saying that you read the burette to the
nearest 0.01 mL, or words to that effect.
On top of all that, the meaning of a burette reading may be subject to
uncertainty due to the fact that the liquid comes out in discrete
drops. There are steps you can take to migitate this. If there are
droplets inside the column, or a thin film wetting the surface, this
is an additional source of uncertainty, including both scatter and
systematic bias.
Last but not least, there will be some uncertainty due to the fact
that the burette may not be a perfect cylinder, and the graduations
may not be in exactly the right places. Industry-standard tolerances
are:
| Capacity / mL | | Tolerance / ml |
| | | Class A | | Class B |
| 10 | | 0.02 | | 0.04 |
| 25 | | 0.03 | | 0.06 |
| 50 | | 0.05 | | 0.10 |
| 100 | | 0.10 | | 0.20 |
The tolerances apply to the full capacity of the burette. It is
likely (but not guaranteed) that the errors will be less if a lesser
amount is delivered from the burette.
At the time you make a reading, it is quite likely that you don’t know
the overall uncertainty, in which case you should just write down the
number with plenty of guard digits.4 Make a note of
whatever calibration information you have, and make a note about the
readability, but don’t say anything about the uncertainty. Weeks or
months later, when you have figured out the overall uncertainty, you
should report it ... and in most cases you should also report the
various things that contributed to it, including things like
readability, quantization errors, systematic biases, et cetera.
6.4 Analyzing an Ensemble of Readings
Suppose we perform an ensemble of measurements, namely 100 repetitions
of the experiment described in section 6.3. The black
vertical bars in Figure 22 are a histogram, showing the
results of a numerical simulation.
One thing to notice is that the measurements, as they appear in my lab
book, have evidently been rounded off. This is of course unavoidable,
since the true value is a continuous, analog variable, while the
indicated value that gets written down must be discrete, and must be
represented by some finite number of digits. See section 8.6
for more about the effect of rounding. We can see that in the figure,
by noticing that only the bins corresponding to round multiples of
0.001 are occupied. The histogram shows data for bins at all
multiples of 0.0002, but only every fifth such bin has any chance of
being occupied.
In figure 22, the magenta line is a Gaussian with the
same mean and standard deviation as the ensemble of measurements. No
deep theory is needed here; we just calculate the mean and standard
deviation of the data and plot the Gaussian. You can see that the
Gaussian is not a very good fit to the data, but it is not too
horribly bad, either. It is a concise but imperfect way of
summarizing the data.
There is a conceptual point to be made here: Suppose we ignore the
black bars in the histogram, and consider only the 100 raw data points
plus the cooked data blob. The question arises, how many numbers are
we talking about?
The answer is 102, namely the 100 raw data points plus the mean and
standard deviation that constitute the raw data blob, i.e. the
Gaussian model distribution, as indicated in the following table:
| Measurement # 1 | is | 39.37 |
| Measurement # 2 | is | 39.371 |
| ... |
| Measurement # 99 | is | 39.373 |
| Measurement # 100 | is | 39.371 |
|
| The model | is | 39.3704 ± 0.0015 |
Table 5: Raw Measurements, Plus the Model
We emphasize that there is only one ± symbol in this entire table,
namely the one on the bottom line, where we describe the model
distribution. In contrast, at the time measurement #1 is made, we
could not possibly know the standard deviation – much less the
uncertainty5 – of
this set of measurements, so it would be impossible to write down
39.37 plus-or-minus anything meaningful. Therefore we just write down
39.37 and move on to the next measurement.
In general, if we have N observations drawn from some Gaussian
distribution, we are talking about N+2 numbers. We are emphatically
not talking about 2N+2 numbers, because it is conceptually not
correct to write down any particular measurement in the form
A±B. People do it all the time, but that doesn’t make it right.
As mentioned in section 5, a distribution is not a
number, and a number is not a distribution.
- Anything you write down in the form x1 = 39.37
represents a plain old number.
- Anything you write down in the form X = 39.3704 ± 0.0015
represents a distribution, not a number.
In the simplest case, namely N=1, it requires three numbers to
describe the measurement and the distribution from which it was drawn.
If we unwisely follow the common practice of recording “the
measurement” in the form A±B, presumably B represents the
standard deviation of the distribution, but A is ambiguous. Does it
represent the actual observed reading, or some sort of estimate of the
mean of the underlying distribution? When we have only a single
measurement, the ambiguity seems mostly harmless, because the
measurement itself may be our best estimate of the mean of the
distribution. Even if it’s not a very good estimate, it’s all we have
to go on.
Things get much stickier when there are multiple observations,
i.e. N≥2. In that case, we really don’t want to have N separate
estimates of the mean of the distribution and N separate estimates
of the standard deviation. That is to say, it just doesn’t make
sense to write down N expressions of the form A±B. The only
thing that makes any sense is to write down the N measurements as
plain numbers, and then separately write down the estimated mean and
standard deviation of the distribution ... as in the table above.
6.5 Standard Deviation versus Uncertainty versus Error
Before leaving the burette example, there is one more issue we must
discuss. It turns out that during my series of simulated experiments,
in every experiment I started out with the exact same volume of
liquid, namely 39.3312 mL, known to very high accuracy. Subsequently,
during the course of each experiment, the volume of liquid will of
course fluctuate, due to thermal expansion and other factors, which
accounts for some of the scatter we see in the data in
figure 22. Imperfect experimental technique and
roundoff error account for additional spread.
Now we have a little surprise. The distribution of measurements is
39.3704 ± 0.0015 mL, whereas the actual amount of liquid was
only 39.3312 mL, which is far, far outside the measured distribution.
So, how do we explain this?
It turns out that every one of the experiments was done with the same
burette, which was manufactured in such a way that its cross-sectional
area is too small by one part per thousand. Therefore it always reads
high by a factor of 1.001, systematically.
This underlines that point that statistical analysis of your
observations will not reveal systematic bias. Standard deviation is
precisely defined and easy to calculate, but it is not equivalent to
uncertaintly, let alone error. For more on this, see
section 13, especially section 13.5 and
section 13.6.
6.6 Example: Decimal Interpolation Between Graduations
Suppose I’m measuring the sizes of some blocks using a ruler. The
ruler is graduated in millimeters. If I look closely, I can measure
the blocks more accurately than that, by interpolating between the
graduations. As pointed out by Michael Edmiston, sometimes the
situation arises where it is convenient to interpolate to the nearest
1/4th of a millimeter. Imagine that the blocks are slightly misshapen
so that it is not possible to interpolate more accurately than that.
Let’s suppose you look in my lab notebook and find a column
containing the following numbers:
Table 6: Length of Blocks, Raw Data
and somewhere beside the column is a notation that all the numbers are
rounded to the nearest 1/4th of a millimeter. That means that each of
these numbers has a roundoff error on the order of ±1/8th of a
millimeter. As always, the roundoff errors are not
Gaussian-distributed. Roundoff errors are one contribution to the
uncertainty. In favorable situations this contribution is
flat-distributed over the interval ±1/8 mm, but the actual
situation may not be nearly so favorable, as discussed in
section 7.12, but let’s not worry about that right now.
If we worshipped at the altar of sig digs, we would say that that the
first number (40) had one “sig dig” and therefore had an uncertainty
of a few dozen units. However, that would be arrant nonsense. The
actual uncertainty is a hundred times smaller than that. The lab book
says the uncertainty is 1/8th of a unit, and it means what it says.
At the other end of the spectrum, the fact that I wrote 40.75 with two
digits beyond the decimal point does not mean that the
uncertainty is a few percent of a millimeter (or less). The actual
uncertainty is ten times larger than that. The lab book says that all
the numbers are rounded to the nearest 1/4th of a millimeter, and it
means what it says.
The numbers in table 6 are perfectly suitable for typing
into a computer for further processing. Other ways of recording are
also suitable, but it is entirely within my discretion to choose
among the various suitable formats that are available.
The usual ridiculous “significant digits rules” would compel me to
round off 40.75 to 40.8. That changes the nominal value by 0.05mm.
That shifts the distribution by 40% of its half-width. Forty percent
seems like a lot. Why did I bother to interpolate to the nearest
1/4th of a unit, if I am immediately forced to introduce a roundoff
error that significantly adds to the uncertainty? In contrast,
writing 3/4ths as .75 is harmless and costs nothing.
Bottom line: Paying attention to the “sig digs rules” is unnecessary
at best. Good practice is to record the nominal value and the
uncertainty separately. Keep many enough digits to make sure there is
no roundoff error. Keep few enough digits to be reasonably
convenient. Keep all the original data. See section 8.2 for more
details.
Even more-extreme examples can be found. Many rulers are graduated in
1/8ths of an inch. This is similar to the example just discussed,
except that now it is convenient to write things to three decimal
places (not just two). Again the sig figs rules mess things up.
More generally: Any time your measurements are quantized with a
step-size that doesn’t divide 10 evenly, you can expect the “sig digs
rules” to cause trouble.
6.7 Readability is Only Part of the Uncertainty
Consider the contrast:
|
Sometimes readability is the dominant contribution to the
uncertainty of the instrument, as when there are only a limited number
of digits on a display, or only a limited number of coarse gradations
on an analog scale.
|
|
Sometimes readability is nowhere near being the
dominant contribution, as in the example in section 6.1, at the
low end of the scale.
|
And another, separate contrast:
|
Sometimes the uncertainty associated with the instrument is
the dominant contribution to the overall uncertainty.
|
|
Sometimes the
instrument is nowhere near being the dominant contribution, for
instance when you hook a highly accurate meter to a signal that is
fluctuating.
|
I’ve seen alleged rules that say you should read instruments by
interpolating to 1/10th of the finest scale division, and/or that the
precision of the instrument is 1/10th of the finest scale division.
In some situations those rules reflect reality, but sometimes they
are wildly wrong.
When choosing or designing an instrument for maximum accuracy, usually
you should arrange it so that the dominant contribution to the overall
uncertainty is is set by some sort of noise, fluctuations, or fuzz.
That makes sense, because if the reading is not fuzzy, you can
usually find a way to apply some some magnification and get more
accuracy very cheaply.
7 Propagation of Uncertainty
7.1 Overview
Consider the following scenario: Suppose we know how to calculate some
result xi as a function of some inputs ai, bi, and ci:
We assume the functional form of f(...) is known. That’s fine as
far as it goes. The next step is to understand the uncertainty. To
do that, we need to imagine that the numbers ai, bi, and ci
are drawn from known distributions A, B, and C respectively, and
we want to construct a distribution X with the following special
property: Drawing an element xi at random from X is the same as
drawing elements from A, B, and C and calculating xi via
equation 6.
This topic is called propagation of uncertainty. The idea is
that the uncertainty “propagates” from the input of f(...) to the
output.
If we are lucky, the distribution X will have a simple form that can
be described in terms of some nominal value ⟨X⟩ plus-or-minus
some uncertainty [X]. If we are extra lucky, the nominal value of
X will be related to the nominal values of A, B, and C by
direct application of the same function f(...) that we saw in
equation 6, so that
| ⟨X⟩ | | = | | f(⟨A⟩, ⟨B⟩, ⟨C⟩) | | (if extra lucky)
|
| (7)
|
Beware that propagation of uncertainty suffers from
three categories of problems, namly Misrepresentation,
Malexpansion, and Correlation. That is: - Misrepresentation: The sig-figs approach cannot even represent
uncertainty to an acceptable accuracy. Representation issues are
discussed in section 8.2. You could fix the representation using
the ⟨A⟩±[A] notation or some such, but then both of the
following problems would remain.
- Malexpansion: The step-by-step first-order approach fails if the
first-order Taylor expansion is not a good approximation, i.e. if
there is significant nonlinearity. The step-by-step approach fails
even more spectacularly if the Taylor series fails to converge. See
e.g. section 7.19, section 7.6, and section 7.5.
- Correlation: The whole idea of a data blob of the form ⟨A⟩±[A]
goes out the window if one blob is correlated with another. See
e.g. section 7.7.
Let’s consider how these issue affect the various steps in the
calculation:
- Step 0: We need a way to represent the uncertainty of three
input distributions A, B, and C.
- Step 1: We need a way to calculate the properties
(including the uncertainty) of the new distribution X.
- Step 2: After we know the uncertainty of X,
we need a way to represent it.
Steps 0 and 2 are representation issues, while step 1 is a
propagation issue. The propagation rules are distinct from the
representation issues, and are very much more complicated. The
propagation rules might fail if the Taylor expansion isn’t a good
approximation ... and might also fail if there are correlations in
the data.
Beware that the people who believe in sig figs tend to express
both the representation rules and the propagation rules in terms
of sig figs, and lump them all together, but this is just two
mistakes for the price of one. As a result, when people speak of
“the” sig figs rules, you never know whether they are talking
about the relatively-simple representation rules, or the more
complicated propagation rules.
|
Sig figs cause people to misunderstand the distinction
between representation of uncertainty and propagation
of uncertainty.
|
|
In reality, when dealing with real raw data
points or artificial (Monte Carlo) raw data points, the
representation issue does not arise. The raw data speaks for
itself.
|
In practice, the smart way to propagate uncertainties is:
-
Use the Crank Three Times™
method, as described in section 7.14. This works for a wide
range of simple problems. This contructs three elements of the
distribution X. If you are lucky, this is a representative sample.
The best thing is, in cases where it doesn’t work, you will almost
certainly know it. That’s because (unless you are very unlucky) you
will get lopsided error bars, or worse, and this tells you a more
powerful method is needed.
-
Use the Monte Carlo method, as described
in section 7.16. This is very easy to do using the spreadsheet
program on your computer. This constructs a representation of the the
distribution X, representing it as a cloud of zero-sized points.
This is tremendously advantageous, because the uncertainty is now
represented by the width of the cloud. The individual points have no
width, so you can use ordinary algebra to calculate whatever you want,
point-by-point, step-by-step. This is very much simpler – and more
reliable – than trying to attach uncertainty to each point and then
trying to propagate the uncertainty using calculus-based first-order
techniques.
In order to really understand the propagation of uncertainty, we
must learn a new type of arithmetic: We will be performing
computations on probability distributions rather than on simple
numbers.
7.2 Simple Example: Multi-Step Arithmetic
This subsection shows the sort of garbage that results if you try to
express the propagation rules in terms of sig figs.
Let’s start with an ultra-simple example
|
x = (((2 + 0.4) + 0.4) + 0.4) + 0.4
(8) |
where each of the addends has an uncertainty of ±10%, normally
and independently distributed.
Common sense suggests that the correct answer is x = 3.6 with some
uncertainty. You might guess that the uncertainty is about 10%, but
in fact it is less than 6%, as you can verify using the methods
of section 7.16 or otherwise.
In contrast, the usual “significant digits rules” give the ludicrous
result x=2. Indeed the “rules” set each of the parenthesized
sub-expressions is equal to 2.
This is a disaster. Not only do the “sig figs rules” get the
answer wrong, they get it wrong by a huge margin. They miss the
target by seven times the radius of the target!
To understand what’s going on here, consider the innermost
parenthesized sub-expression, namely (2 + 0.4).
- Step 1 (propagation): The sum is 2.4, obviously. Let’s assume
this is the nominal value of the result-distribution. Let’s also
assume the uncertainty is calculated in the usual way, so that the
uncertainty on the sum is at least as great as the uncertainty on the
addends. Neither of these assumptions is entirely safe, but let’s
assume them anyway, so as to construct a best-case scenario.
- Step 2 (representation): Since the sum (2.4) has more
uncertainty than the first addend (2), it should be represented by
at most the same number of sig figs, so we round it off. We
replace 2.4 with 2. This is a disaster.
Repeatedly adding 0.4 causes the same disaster to occur repeatedly.
The fundamental issue here is that the sig figs rules require you to
keep rounding off until roundoff error becomes the dominant
contribution to the uncertainty. This is a representation issue, but
it interacts with the propagation issue as follows: The more often you
apply the sig figs representation rules, the worse off you are ... and
the whole idea of propagation requires you to do this at every step of
the calculation.
Rounding off always introduces some error. This is called roundoff
error or quantization error. Again: One of the fundamental problems
with the sig figs rules is that in all cases, they demand too much
roundoff.
This problem is even worse than you might think, because there is no
reason to assume that roundoff errors are random. Indeed, in
equation 8 the roundoff errors are not random at all; the
roundoff error is 0.4 at every step. These errors accumulate
linearly. That is, in this multi-step calculation, the overall
error grows linearly with the number of steps. The errors do not
average out; they just accumulate. Guard digits are a good way to
solve part of the problem, as discussed in section 7.3 and section 8.8.
7.3 Guard Digits (Preview)
Let’s take another look at the multi-step calculation in
equation 8. Many people have discovered that they can
perform multi-step calculations with much greater accuracy by using
the following approach: At each intermediate step of the calculation,
the use more digits than would be called for by the sig figs rules.
These extra digits are called guard digits, as discuseed in See
section 8.8. Keeping a few guard digits reduces the
roundoff error by a few orders of magnitude. When in doubt, keep
plenty of guard digits on all numbers you care about.
Guard digits do not, however, solve all the world’s problems. In
particular, suppose you were using the sig figs rules at every step
(as in section 7.2) in an attempt to perform
“propagation of error”. (Propagation is, after all, the topic of
this whole section, section 7). The problem is,
step-by-step first-order propagation is almost never reliable, even if
you use plenty of guard digits. The first reason why it is unreliable
is that the first-order Taylor approximation often breaks down.
Furthermore, even if you could fix that problem, the approach fails if
there are correlations. There’s a proverb that says imperfect
information is better than no information, but that proverb doesn’t
apply here, because we have much better ways of getting information
about the uncertainty, such as the Crank Three Times™
method.
When there is noise (i.e. uncertainty) in your raw data, guard digits
don’t make the raw noise any smaller ... they just make the roundoff
errors smaller.
Roundoff error
is just one among many sources
of error and uncertainty.
|
|
|
|
Experimental error in the raw data
is just one among many sources
of error and uncertainty.
|
|
|
|
See section 8.8 and section 8.9 for
more discussion of guard digits. See section 12 for
more discussion of various contributions to the uncertainty.
7.4 Example: Beyond First Order: 1 to the 40th Power
Exponentials show up in a wide variety of real-life situations. For
example, the growth of bacteria over time is exponential, under
favorable conditions.
As a simple example, let x=1 and consider raising it to the 40th
power, so we have y = x40. Then y=1. It couldn’t be simpler.
Next, consider x that is only “near” 1. We draw x from the
rectangular distribution 1.0±0.05. We compute y = x40, and
look at the distribution over y-values. Roughly speaking, this is
the distribution over the number of bacteria in your milk, when there
is a distribution over storage temperatures. The results are
diagrammed in figure 23 and figure 24.
Note that figure 23 is zoomed in to better portray
the red curve, at the cost of clipping the blue spike; the
distribution over x actually peaks at dP/dx=10.
As you can see, the y-values are spread over the interval from 0.13
to 7.04. Hint: that’s 1/e2 to e2.
What’s worse is that the distribution is neither rectangular nor
Gaussian, not even close. It is strongly peaked at the low end. The
HWHM is very small, while the overall width is enormous. The mode of
the distribution is not 1, the mean is not 1, and the median is not
1. So the typical abscissa (x=1) does not map to the typical ordinate.
This is an example where Crank Three Times gives spectacularly
asymmetric error bars, which is a warning. There are lots of
distributions in this world that cannot be described using the notion
of “point plus error bars”.
This is not primarily a «sig figs» problem. However, as usual, no
matter what you are doing, you can always make it worse by using «sig
figs». The uncertainty on y is larger than y, so «sig figs»
cannot even represent this result! If you tried, you would end up with
zero significant digits.
Also, the usual propagation rules, as taught in conjunction with «sig
figs», say that x multiplied by x has the same number of «sig
figs» as x. Do that 40 times and you’ve still got the same
number. So the «sig figs» alleged uncertainty on y is just 0.05
... but reality begs to differ.
7.5 Example: Beyond First Order: Momentum and Energy
Suppose we have a bunch of particles in thermal equilibrium. The x
component of momentum is Gaussian distributed, with mean 0 and
standard deviation √mkT. The distribution is the same for the
y and z components. For simplicity, lets choose units such that
m=1, and momentum is equal to velocity. A scatter plot of the x
and y components is shown in figure 25.
 Figure 25
Figure 25: Thermal Distribution of Velocities
The kinetic energy of any given particle is p2/(2m). The
uncertainty in the mass is negligible in this situation. This
situation is simple enough that the right answer can be found
analytically, as some guy named Maxwell did in the mid-1800s. You can
also find the right answer using Monte Carlo techniques. If the
situation were even slightly more complicated, Monte Carlo would be
the only option.
If you calculate the energy for an ensemble of such particles, the
cumulative probability is shown in figure 26.
Similarly, the probability density distribution is shown in
figure 27. The dashed red line shows the exact
analytic result, i.e. the Maxwell-Boltzmann distribution.
|
|
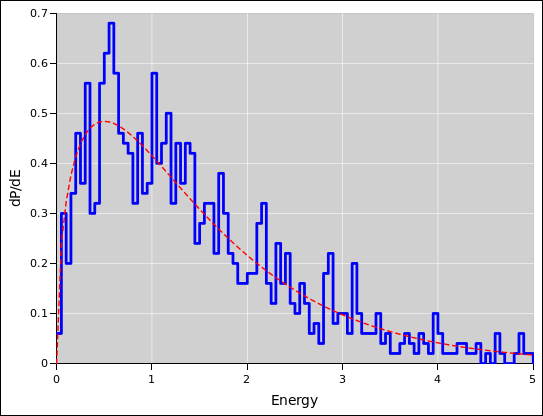
|
|
Figure 26: Maxwell-Boltzmann Distribution of Energy (3D)
|
|
Figure 27: Maxwell-Boltzmann Distribution of Energy (3D)
|
|
Cumulative Probability
|
|
Probability Density
|
If you tried to obtain the same result using step-by-step propagation
of uncertainty, starting from the thermal distribution of velocities,
things would not go well. Using the procedure given in
section 7.20.2, you would find that the relative
uncertainty was infinite. Forging ahead, applying the formula without
regard to the provisos in the rule, this would imply an energy of zero
plus-or-minus infinity. This is nowhere close to the right answer.
We can discuss the failure of the step-by-step approach in terms of
the unholy trinity of Misrepresentation, Malexpansion, and
Correlation.
- Sig figs cannot represent the distribution of velocities. It
cannot represent 0±√mkT or anything remotely like that.
- The first-order Taylor expansion fails. There is no first-order
term in the expansion for E in terms of p.
- Correlation issues are not a problem in this situation.
This example and the next one were chosen because they are simple,
and because they make obvious the failure of the step-by-step
approach. Beware that in situations that are even slightly more
complex, the step-by-step approach will fail and give you wrong
answers with little or no warning.
7.6 Example: Non-Differentiable: Time = Distance / Rate
Suppose we have a long, narrow conference table. We start a particle
in the middle of the table. At time t=0 we give it a velocity based
on a thermal distribution, zero plus-or-minus √kT/m.
Thereafter it moves as a free particle, moving across the table. We
want to know how lot it takes before the particle falls off the edge
of the table. A scatter plot of the velocity is shown in figure 25. For present purposes, only the x component
matters, because the table is narrow in the x direction and very
very long in the y direction.
If we take the Monte Carlo approach, this is an ultra-simple “time =
distance / rate” problem. For each element of the ensemble, the time
to fall off is:
where w is the width of the table, and v is the velocity.
The cumulative probability distribution is shown in figure 28. A histogram of the probability density is shown in
figure 29.
|
|
|
|
Figure 28: Time to Fall Off
|
|
Figure 29: Time to Fall Off
|
|
Cumulative Probability
|
|
Probability Density
|
Beware that not all the data is visible in these figures. Given an
ensemble of 1000 points, it would not be uncommon to find the maximum
time to be greater than 1000 units, or indeed greater than 2000 units.
The maximum-time point corresponds to the minimum-velocity point, and
velocites near zero are not particularly uncommon. That means that
the probability density distribution converges only very slowly toward
zero at large times. As a consequence, the mean of the distribution
is large, vastly larger than the mode. The standard deviation could
be in the hundreds, which is vastly larger than the HWHM.
We can contrast the Monte Carlo approach to step-by-step first-order
propagation. The latter fails miserably. In the first step, we need
to take the absolute value of the velocity. To calculate the
uncertainty, we need the derivative of this, evaluated at the origin,
but alas absolute value is not a differentiable function at the
origin. In the second step, we need to take the reciprocal, which is
not even a function at the origin, much less a differentiable
function.
This example and the previous one were chosen because they are simple,
and because they make obvious the failure of the step-by-step
approach. Beware that in situations that are even slightly more
complex, the step-by-step approach will fail and give you wrong
answers with little or no warning.
Extensions: This simple example is part of a larger family. It
can be extended and elaborated in various ways, including:
- Motion in 2 or 3 dimensions, not just one.
- Uncertainty in the initial position, not just velocity. At some
level, this is required by the Heisenberg uncertainty principle.
- Motion in the presence of a nontrivial potential. Example: time
to fall over, for the 1D motion of a thin flat slab balanced on its
edge. Example: time to fall over, for the 2D motion of a pencil
balanced on its point.
7.7 Example: Correlated Data: Charge-to-Mass Ratio
Suppose we want to know the charge-to-mass ratio for the electron,
i.e. the e/m ratio. This is useful because it shows up in lots of
places, for instance in the formula for the cyclotron frequency (per
unit field).
We start by looking up the accepted values for
e and m, along with the associated uncertainties. Here are the
actual numbers, taken from the NIST website:
|
e | | = | | 1.602176565×10−19 coulomb |
| | | | | with 22 parts per billion relative uncertainty |
| m | | = | | 9.10938291×10−31 kg |
| | | | | with 44 ppb relative uncertainty
|
| (10)
|
At this point it is amusing to calculate the e/m ratio by following
the propagation-of-error rules that you see in textbooks. Ask
yourself, What is the calculated uncertainty for the e/m ratio, when
calculated this way? Choose the nearest answer:
-
- a) 22 ppb
- b) 33 ppb
- c) 44 ppb
- d) 50 ppb
- e) 66 ppb
Note: Ordinarily I play by the rule that says you are
expected to use everything you know in order to get the real-world
right answer. Ordinarily I despise questions where knowing the
right answer will get you into trouble. However ... at the moment
I’m making a point about the method, not trying to get the right
answer, so this rule is temporarily suspended. You’ll see why
shortly.
If we carry out the calculation in the usual naïve way, we assume
the uncertainties are uncorrelated, so we can add the relative
uncertainties in quadrature:
|
relative uncertainty | | = | | |
| | | = | | 49 ppb | | ☠
|
| (11)
|
so the full result is
|
e/m | | = | | 1.758820088×1011 C/kg |
| | | | | with 49 ppb uncertainty | | ☠
|
| (12)
|
We can contrast this with the real-world correct value:
|
1.75882008×1011 C/kg | |
| | | | | with only 22 ppb uncertainty
|
| (13)
|
The real uncertainty is vastly less than the naïvely-calculated
uncertainty.
We can understand this as follows: The accepted values for e and m are
correlated. Virtually 100% correlated.
Simple recommendation: If you want to calculate e/m, don’t just look
up the values for e and m separately. Use the NIST website to
look them up jointly along with the correlation coefficient.
Before we go on, lets try to understand the physics that produces the
high correlation between e and m. It’s an interesting story: You
could measure the mass of the electron directly, but there’s not much
point in doing so, because it turns out that indirect methods work
much better. It’s a multi-step process. The details are not super
important, but here’s a slightly simplified outline of the process.
- A) The fine
structure constant is measured to 0.32 ppb relative uncertainty.
- B) The Rydberg
constant is measured to 0.005 ppb.
- C) The Rydberg constant is equal to m e4 / 8 є02 h3 c
and the fine-structure constant is e2 / 2 є0 h c.
Combining α3/Ry gives e2/m to 0.96 ppb. It hardly matters
whether they are correlated or not, since the uncertainty is
dominated by the uncertainty in α3. Note that the speed of
light is exact, by definition, so it does not contribute to the
uncertainty.
- D) The charge on the electron is measured to 22 ppb.
- E) If you want the e/m ratio, divide e2/m by e. The uncertainty in
e/m is dominated by the uncertainty in e.
- F) To find the mass, calculate e2 (using the measured charge
directly) then divide by the e2/m value obtained in item (c)
above. The uncertainty is 44 ppb, dominated by the uncertainty in
e2.
Bottom line: Whenever you have two randomly-distributed quantities and
you want to combine them – by adding, subtracting, multiplying,
dividing, or whatever – you need to find out whether they are
correlated. Otherwise you will have a hard time calculating the
combined uncertainty.
7.8 Example: Solving a Quadratic Polynomial for the pH
Figure 30 shows pH as a function of concentration, for
various pKa values, including weak acids and strong acids, as well as
intermediate-strength acids, which are particularly interesting.
 Figure 30
Figure 30: pH versus Concentration for Various p
Ka Values
This is obviously not a contrived example. There are plenty of good
reasons for preparing a plot like this. For present purposes,
however, we are not particularly interested in the meaning of this
figure, but rather in the process of computing it. (If you are
interested in the meaning, please see
reference 13.)
For simplicity, we temporarily restrict attention to the parts of
figure 30 that are not too near the top. That is, we focus
attention on solutions that are definitely acidic, with a pH well
below the pH of water. (This restriction will be lifted in
section 7.9.)
In this regime, the relevant equation is:
|
[H+]2 + Ka [H+] − Ka CHA = 0
| |
| (14)
|
Equation 14 is a quadratic polynomial, where the
coefficients are:
|
a | | = | | 1 |
| b | | = | | Ka |
| c | | = | | −Ka CHA |
| x | | = | | [H+]
|
| (15)
|
It has one positive root and one negative root, as we shall see. For
more on where this comes from and what it means, see reference 13 and references cited therein.
Let’s plug in the numbers for our dilute solution of a strong acid:
|
Ka | | = | | 5.666×104 |
| CHA | | = | | 10−6
|
| (16)
|
Let’s use the numerically stable version of the quadratic formula, as
discussed in reference 14:
|
| |
xbig | | = | | | | (assuming a ≠ 0) | |
(17a)
|
|
| |
xsmall | | = | | | | | |
(17b)
|
|
where sgnL(x) is the left-handed sign-function, which is defined to
be −1 whenever x is less than or equal to zero, and
+1 otherwise. In most computer languages it can be implemented as
(2*(x>0)-1). (Do not use the regular sgn() function, which is
zero at zero.) The names “small” and “large” are based on the
absolute magnitude of the roots.
That gives us:
|
{xbig, xsmall} | | = | | {−5.666×104, 10−6}
|
| (18)
|
You can see that this is definitely a “big root / small root”
situation, so you need to use the smart version of the quadratic
formula, for reasons explained in reference 14.
Only the positive root in equation 18 makes
sense. Taking the logarithm, we find
|
pH | | := | | −log10([H+]) |
| | | = | | −log10(xsmall) |
| | | = | | 6
|
| (19)
|
Note that the “small root” here is not some minor correction term;
it is the entire answer.
For a discussion of the lessons we can learn from this example,
see section 7.11.
We revisit this example again in section 7.23, in
connection with the rules for step-by-step first-order propagation of
uncertainty.
7.9 Example: Solving a Cubic Polynomial for the pH
We now consider the full pH versus concentration diagram, without the
restrictions on strength and/or concentration imposed in
section 7.9.
The full curves in figure 30 were computed by solving the
following equation.
|
[H+]3 + Ka [H+]2 − (Kw + Ka CHA) [H+] − Ka Kw | | = | | 0
|
| (20)
|
That’s a cubic, with one positive root and two negative roots. For
more on where this comes from and what it means, see
reference 13.
It is easy to solve the equation with an iterative root-finding
algorithm.
In contrast, beware that standard “algebraic” formulas for solving
the cubic can give wrong answers in some cases. Depending on details
of the implementation, the formulas can be numerically unstable. That
is to say, the result gets trashed by roundoff errors. Specifically:
I tried using the standard library routine
gsl_poly_complex_solve_cubic() and it failed
spectacularly for certain values of pK_a and pC_HA. Some of the
alleged results were off by multiple orders of magnitude. Some of the
alleged results were complex numbers, even though the right answers
were real numbers. It might be possible to rewrite the code to make
it behave better, but that’s not a job I’m eager to do.
For a discussion of the lessons we can learn from this example,
see section 7.11.
7.10 Another Example: Multi-Step Relativity
7.10.1 Correct Direct Calculation
Once upon a time, at Acme Anvil company, there was an ensemble of
particles. The boss wanted a relativistically-correct calculation of
the kinetic energy. He especially wanted the mean and standard
deviation of the ensemble of kinetic-energy values.
The boss assigned two staffers to the task, Audrey and Alfred. Audrey
worked all morning computing the total energy E(v) and the rest
energy E(0) for each particle. Then Alfred worked all afternoon,
subtracting these two quantities to find the kinetic energy for each
particle.
In all cases, Audrey and Alfred used the relativistically correct
formulas, namely
|
| | energy: | | E(v) | | = | | m c2 cosh(ρ) |
| rapidity: | | ρ | | = | | atanh(v/c) |
| kinetic energy: | | Ekin | | = | | E(v) − E(0) |
| speed of light: | | c | | = | | 299792458 m/s (exactly) |
|
(21) |
The following data describes a typical particle in the ensemble:
|
| | mass: | | m | | = | | 5/3 kg |
| velocity: | | v | | = | | 4/3 m/s |
|
(22) |
For this particle, Audrey calculated the following results:
|
E(0) | | = | | 149792529789469606.6666667 ... joule |
| E(v) | | = | | 149792529789469608.1481482 ... joule |
| (23)
|
where both of those numbers are repeating decimals.
Later, Alfred subtracted those numbers to obtain
|
Ekin | | = | | 1.4814815 ... joule |
| (24)
|
which is again a repeating decimal.
After calculating the kinetic energy for all the particles, Alfred
calculated the mean and standard deviation, namely:
|
Ekin | | = | | 1.481 joule ± 0.5% |
| | | = | | 1.481(7) joule
|
| (25)
|
which is in fact the correct answer.
7.10.2 Unsuccessful Double-Precision Direct Calculation
Meanwhile, across the street at Delta Doodad Company, they needed
to do the exact same calculation. The boss assigned Darla and Dave to
do the calculation.
Darla calculated E(v) and E(0) using a spreadsheet program, which
represents all numbers using IEEE double-precision floating point.
For the typical particle described in
equation 22, she obtained:
|
E(0) | | = | | 1.4979252978946960E+17 joule |
| E(v) | | = | | 1.4979252978946960E+17 joule |
| (26)
|
These numbers cannot be represented to any greater accuracy using IEEE
double precision.
When Dave subtracted these numbers, he found the kinetic energy was
zero. In fact the apparent kinetic energy was zero for all particles.
When he calculated the mean and standard deviation, they were both
zero. Alfred suspected that 0±0 was not the correct answer, but
given what he had to work with, there was no way for him to compute a
better answer.
The problem is that IEEE double precision can only represent about 16
decimal digits, whereas at least 20 digits are needed to obtain a
useful answer in this case. If you use less than 20 digits, the
roundoff error will be unacceptably large. (By way of contrast,
across the street, Audrey used 25 digits just to be on the safe side.)
7.10.3 Gross Failure: Sig Figs
Meanwhile, down the street at General Gadget Company, they needed
to do the same calculation. The boss was a big fan of sig figs. He
demanded that everybody adhere to the sig figs rules.
The boss assigned Gail and Gordon to the task. In the morning, Gail
calculated the total energy and rest energy. She noticed that there
was some uncertainty in these numbers. The relative uncertainty was
about 0.5%. So for the typical particle described in
equation 22, she obtained:
|
E(0) | | = | | ⎛
⎜
⎝ | | | 1.497925297894696066666667 ... |
| ± | 0.007 |
| ⎞
⎟
⎠ | × 1017 joule |
|
| E(v) | | = | | ⎛
⎜
⎝ | | | 1.497925297894696081481482 ... |
| ± | 0.007 |
| ⎞
⎟
⎠ | × 1017 joule |
|
| (27)
|
In accordance with the usual sig figs rules, Gail rounded off these
numbers, as follows:
|
E(0) | | = | | 1.50 × 1017 joule |
| E(v) | | = | | 1.50 × 1017 joule |
| (28)
|
Gail’s reasons for rounding off included:
-
She felt obliged to communicate the uncertainty to Gordon.
Writing down a large number of digits
(as Audrey did in section 7.10.1)
would “imply” – via
the sig-figs rules – a very small uncertainty, which in this
case would be quite wrong. It would be downright dishonest.
- Equation 28 “looks nicer” than
equation 27.
- She knew the boss would get angry and call call her
“numerically ignorant” if she wrote down a bunch of trailing digits,
i.e. uncertain, irreproducible digits.
All in all, it was “obvious” to Gail that equation 28 was the right way to express things.
In the afternoon, Gordon subtracted these numbers. He found that every
particle had zero kinetic energy.
Based on the uncertainty in the numbers he was given, he tried to
apply the propagation-of-error rules. Since Gail did not report any
correlations, he assumed all her results were uncorrelated, so that
the rules presented in section 7.20 could be
applied. On this basis, he estimated that the uncertainty in the
difference was about ± 1×1015. So Gordon could have
reported his result as 0± 1×1015 joule.
That’s the wrong answer. Gordon’s estimate of the mean is wrong by
about 200 standard deviations. That’s a lot. Gordon’s estimate of the
standard deviation is also off by about seventeen orders of magnitude.
That’s a lot, too.
One problem is that Gail didn’t feed Gordon enough digits. She actually
calculated enough digits, but she felt obliged to round off her
results, in accordance with the sig figs rules. This illustrates a
general principle:
No matter what you are doing,
you can always make it worse by using sig figs.
|
|
|
|
Another problem is that for each particle, Gail’s numbers for E(v)
and E(0) have very highly correlated uncertainties. Therefore
Gordon’s application of the propagation-of-error rules was invalid.
Thirdly, just to add insult to injury: The sig-figs method does not
provide any way to represent 0 ± 1×1015, so Gordon could not
find any way to report his results at all. The boss wanted a sig-figs
representation, but no such representation was possible.
7.10.4 Algebraic Simplification
Meanwhile, across town at Western Widget Company, yet another company
was faced with the same task. At this company, they noticed that
equation 21 implies that:
|
Ekin | | = | | m c2 [cosh(ρ) − 1] |
| | | = | | |
| (29)
|
where on the second line we have used some trigonometric identities.
Both lines in equation 29 share an important property: the
factor in square brackets is a purely mathematical function. The
function can be defined in terms of a subtraction that involves no
uncertainty of any kind. In contrast, if you were to multiply through
by m c2 before subtracting, you would then face the problem of
subtracting two things that not only have some uncertainties (because
of the uncertainty in m) but would have highly correlated
uncertainties.
It must be emphasized that equation 29 is relativistically
correct; no approximations have been made (yet).
Since the task at hand involves ρ values that are very small
compared to 1, the following approximations are good to very high
accuracy:
|
sinh(ρ) | | = | | ρ + ρ3 / 6 | + | ⋯ |
| cosh(ρ) | | = | | 1 + ρ2 / 2 | + | ⋯ |
| tanh(ρ) | | = | | ρ − ρ3 / 3 | + | ⋯ |
| (30)
|
You can check that these approximations are consistent with each other
to third order in ρ or better, in the sense that they uphold the
identities tanh= sinh/cosh and cosh2 − sinh2 = 1.
Plugging into equation 29 we find that, with
more than enough accuracy,
|
Ekin | | = | | m c2 [ρ2 / 2] | + | ⋯ |
| | | = | | m v2 / 2 | + | ⋯
|
| (31)
|
which allows us to calculate the kinetic energy directly. No
subtractions are needed, and ordinary floating-point arithmetic gives
us no roundoff-error problems. The next term in the series is smaller
than the Ekin by a factor of v2/c2, as you can easily verify.
We apply this formula to all the particles, and then calculate the
mean and standard deviation of the results. The answer is Ekin =
1.481(7) joule, which is identical to the result obtained by
other means in section 7.10.1.
7.11 Discussion: Loss of Significance
The pH examples in section 7.8 and section 7.9 are
obviously real-world examples. They are typical of examples that come
up all the time, in many different situations, ranging from astronomy
to zoology.
The relativity example in section 7.10 is a bit
more contrived, but it illustrates an important theoretical point
about the relationship between special relativity and classical
dynamics. It is representative of a wider class of problems ... just
simplified for pedagogical purposes.
There are a number of lessons we can learn from these examples:
- Something that purports to be an “exact” closed-form solution
is not exact at all if you have to evaluate it using floating point
numbers or other rounded-off numbers. Ironically, in practice, an
approximate and/or iterative solution might be much more accurate than
the purportedly “exact” formula.
- In section 7.8, even the lame “textbook” version
of the quadratic formula would have worked if all of the calculations
had been done using double precision. We only got into real trouble
when we copied down the numbers and rounded them off to some «common
sense» number of digits.
Therefore: When using a calculator or any kind of computer, it is good
practice to leave the numbers in the machine (rather than writing them
down and keying them in again later). Learn how to use the STORE and
RECALL functions on your calculator. Most machines use at least 15
digits, which is usually more than you need, but since keeping them is
just as convenient as not keeping them, you might as well keep them
all. (In contrast, writing the numbers down and keying them in again
is laborious and error-prone. You will be tempted to round them off.
Even the effort of deciding how much roundoff is tolerable is more
work than simply leaving the numbers in the machine.)
In the spirit of “check the work”, it is reasonable to write down
intermediate results, but you should leave the numbers in the machine
also. When you recall a number from storage, you can check to see
that it agrees with what you wrote down.
- On the other hand, the library function used in
section 7.8 fails, even though it is using IEEE double
precision.
|
Double precision is not infinite precision.
|
|
|
|
- These failures serve as a reminder of the difference between
uncertainty and significance. The internal calculations, if they are
to have any hope of working, require a large number of digits, out of
all proportion to the uncertainty of the inputs and/or the required
tolerance on the outputs.
To put it bluntly: If you see an expression of the form:
|
X | | = | | ⎛
⎜
⎝ | | | 1.497925297894696 ... |
| ± | 0.01 |
| ⎞
⎟
⎠ |
| | (incomplete)
|
| (32)
|
you should not assume it is safe to round things off. It may be that
such a number already has too few digits. It may already have been
rounded off too much.
Equation 32 is marked “incomplete” for the following
reason: Suppose you need to write down something to represent the
distribution X. The problem is, because of the correlations, it is
not sufficient to report the variance; you
need to report the covariances as well. The equation as it stands is
not wrong, but without the covariances it is incomplete and possibly
misleading.
Not that the ± notation can only represent the variance (or,
rather, the square root thereof), not the covariances, so it cannot
handle the task when there are nontrivial correlations.
- One way a loss of significance can occur is via
accumulation of small errors in a multi-step calculation,
as in section 7.12.
- Another very common way a loss of significance can occur is via
“small differences between large numbers”. More specifically:
- If you have a small difference between large numbers and the
fluctuations are uncorrelated, you suffer from a noise
amplifier.
In the relativity example considered in
section 7.10, E(v) is in fact highly correlated
with E(0). I know (based on how the particles were prepared) that
there is some uncertainty in the mass of the particle. A factor of
mass is common to both of the terms that are being subtracted. The
uncertainty in the particle velocity is relatively small, so all in
all there is nearly 100% correlation in the uncertainties. (There is
of course no uncertainty in the speed of light, since it is 299792458
m/s by definition.)
- If you have a small difference between large numbers and the
fluctuations are highly correlated, then the intrinsic noise is
smaller than it looks, but you suffer from a roundoff error
amplifier.
It is all-too-common to find expressions for the roots of a polynomial
that depend on subtracting numbers that are highly correlated.
- The technique of restructuring a calculation so as to avoid a
loss of significance falls under the heading of “numerical
methods”. There are entire books devoted to the subject,
e.g. reference 15.
The same idea can be applied to experiments, not just calculations.
For example, to avoid a problem with small differences between large
numbers, you can use null measurements, differential
measurements, bridge structures (such as a Wheatstone bridge),
et cetera.
- Expanding things to lowest order is one of the most commonly
used tools in the scientist’s toolbox.
- It must be emphasized that when Audrey wrote down her numbers for
E(v) and E(0), she did not know the uncertainty. This is typical
of a great many real world situations: Often you need to write down a
number when the uncertainty is not known ... and may not be know until
weeks or months later, if at all.
As mentioned in item 4, my advice is: If you have a
number that ought to be written down, write it down. Just write it
down already. You can worry about the uncertainty later, if
necessary. Write down plenty of guard digits. The number of digits
you write down does not imply anything about the
uncertainty, precision, tolerance, significance, or anything else.
- Contrary to what what Gail’s boss was telling her, you are
not obliged to attach an implicit (or explicit) uncertainty to
numbers you write down. If you have an ensemble of numbers, you
might be able to summarize it in terms of a mean and a
standard deviation, but you might not ... and even if you are able
to summarize it, you are not obliged to. The ensemble speaks for
itself, better than any summary ever could. Adding the width of
the error bars to the width of the ensemble makes things very much
worse, as discussed in section 5.2 and
reference 2. In section 7.10.1 Alfred was able to calculate the ensemble
of kinetic energy values just fine without assigning any
uncertainty to Audrey’s E(v) and E(0) numbers.
Indeed, in section 7.10.3, Gail’s uncertainty numbers
were in some hyper-technical sense correct, but they were highly
misleading. They were worse than nothing, because the correlations
were not taken into account.
- It really makes me cringe when students get points taken away
and get called “numerically ignorant” for doing exactly the right
thing, i.e. keeping plenty of guard digits.
7.12 Example: Signal Averaging: Extracting a Signal from Noise
There are lots of situations where the uncertainty in the final answer
is less than the uncertainty in the raw data.
This can be understood in terms of “signal to noise” ratio. When we
process lots of data, if we do things right, the signal will
accumulate faster than the noise. (Conversely, if we don’t do things
right, the accumulated errors can rapidly get out of hand.)
We now consider an example that illustrates this point. For
simplicity, we assume the raw data is normally distributed and
uncorrelated, as shown in figure 31. The spreadsheet
for creating this figure is in reference 16. In this section
we assume the analysis is done correctly; compare section 7.13.
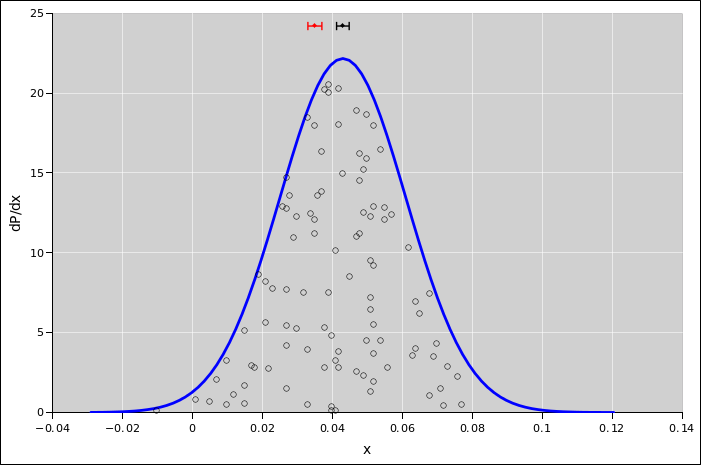 Figure 31
Figure 31: Extracting a Signal from Noisy Data
Specifically, each data point is drawn from a Gaussian distribution
that has a width of 0.018 units. Suppose we run the experiment many
times. On each run, we take the average of 100 points. We know the
average much more accurately than we know any particular raw data
point. In fact, if we look at all the runs, the averages will have a
distribution of their own, and this distribution will have a width of
only 0.0018 units, ten times narrow than the distribution of raw data
points. The distribution of averages is represented by the single
black point with error bars at the top of figure 31.
(This is a cooked data point, not a raw data point.)
We can say the same thing using fancy statistical language. Each run
is officially called a sample. Each sample contains N raw
data points. We assume the points are IID, normally distributed. We
compute the mean of each sample. Theory tells us that the
sample means behave as if they were drawn from a Gaussian
distribution, which will be narrower than the distribution of raw
data, narrower by a factor of √N.
7.13 Example: The Effect of Roundoff Error
Let’s re-analyze the data from section 7.12. In particular,
let’s consider the effect of roundoff errors that occur while we are
calculating the average. Even though the raw data is normally
distributed and IID, the roundoff errors will not be normally
distributed, and if we’re not careful this can lead to serious
problems.
We denote the ith raw data point by ai. It is drawn
from a distribution A that has some uncertainty σA.
Next, we round off each data point. That leaves us with some new
quantity bi. These new points behave as if they were drawn from
some new distribution B.
The new uncertainty σB will be larger than σA, but we
don’t know how much larger, and we don’t even know that distribution
B can be described as a Gaussian (or any other two-parameter model).
It may be that B is a viciously lopsided non-normal distribution
(even though A was a perfectly well-behaved normal distribution).
|
For normally-distributed errors, when you add two numbers,
the absolute errors add in quadrature, as discussed in section 7.20. That’s good, because it means errors accumulate
relatively slowly, and errors can be reduced by averaging.
|
|
For a
lopsided distribution of errors, such as can result from roundoff, the
errors just plain add, linearly. This can easily result in disastrous
accumulation of error. Averaging doesn’t help.
|
This is illustrated by the example worked out in the “roundoff”
spreadsheet (reference 16), as we now discuss. The first few
rows and the last few rows of the spreadsheet are reproduced here. The
numbers in red are seriously erroneous.
| | | raw data | — Alice — | — Bob — | — Carol — |
| 1 | | 0.062 | | | | 0.062 | ± | 0.018 | | 0.062 | ± | 0.018 | | 0.06 | ± | 0.02 |
| 2 | | 0.036 | | | | 0.098 | ± | 0.025 | | 0.098 | ± | 0.025 | | 0.10 | ± | 0.03 |
| 3 | | 0.030 | | | | 0.128 | ± | 0.031 | | 0.128 | ± | 0.031 | | 0.13 | ± | 0.03 |
| 4 | | 0.026 | | | | 0.154 | ± | 0.036 | | 0.154 | ± | 0.036 | | 0.16 | ± | 0.04 |
| ... | |
| 98 | | 0.026 | | | | 4.285 | ± | 0.178 | | 4.36 | ± | 0.18 | | 3.4 | ± | 0.2 |
| 99 | | 0.044 | | | | 4.329 | ± | 0.179 | | 4.40 | ± | 0.18 | | 3.4 | ± | 0.2 |
| 100 | | 0.021 | | | | 4.350 | ± | 0.180 | | 4.42 | ± | 0.18 | | 3.4 | ± | 0.2 |
| | |
| average: | .0435 | ± | 0.0018 | | .0442 | | | .034 | |
| | | = | .0435 | ± | 4.1%
| |
The leftmost column is a label giving the row number. The next column
is the raw data. You can see that the raw data consists of numbers
like 0.048. As usual, the raw data points have no width whatsoever.
However, the distribution from which these numbers were drawn has a
width of 0.018. You can see that we are already departing from the
usual “significant figures” hogwash. If you believed in sig figs,
you would attribute considerable uncertainty to the second decimal
place in each raw data point, and you would not bother to record the
data to three decimal places.
In contrast, in reality, it is important to keep that third decimal
place, for reasons that will become clear very soon. We are going to
calculate the average of 100 such numbers, and the average will be
known tenfold more accurately than any of the raw inputs.
To say the same thing in slightly different terms: there is in fact an
important signal – a significant signal – in that third decimal
place. The signal is obscured by noise; that is, there is a poor
signal-to-noise ratio. Your mission, should you decide to accept it,
is to recover that signal.
This sort of signal-recovery is at the core of many activities in real
research labs, and in industry. On ordinary GPS receiver depends on
signals that are hundreds of times less powerful than the noise (SNR
on the order of -25 dB). The second thing I ever did in a real
physics lab was to build a communications circuit that picked up a
signal that was ten million times less powerful than the noise (SNR =
-70 dB). The JPL Deep Space Network deals with SNRs even worse than
that. Throwing away the signal at the first step by “rounding” the
raw data would be a Bad Idea.
Take-home message #1: Signals can be dug out from the noise.
Uncertainty is not the same as insignificance. A digit that is
uncertain (and many digits to the right of that!) may
well carry some significance that can be dug out by
techniques such as signal-averaging. Given just a number and its
uncertainly level, without knowing the context, you cannot say whether
the uncertain digits are significant or not.Take-home message #2: An expression such as 0.048 ± 0.018
expresses two quantities: the value of the signal, and an
estimate of the noise. Combining these two quantities into a single
numeral by rounding (according to the “significant figures rules”) is
highly unsatisfactory. In cases like this, if you round to express
the noise, you destroy the signal.
Now, returning to the numerical example: I assigned three students
(Alice, Bob, and Carol) to analyze this data. In the data table, the
first column under each student’s name is a running sum. The second
column is a running estimate of the uncertainty of the running sum.
Alice didn’t round any of the raw data or intermediate results. She
got an average of
and the main value (0.0435) is the best that could be done given the
points that were drawn from the ensemble. (The error-estimate is a
worst-case error; the probable error is somewhat smaller.)
Meanwhile, Bob was doing fine until he got to row 31. At that point
he decided it was ridiculous to carry four figures (three decimal
places) when the estimated error was more than 100 counts in the last
decimal place. He figured that if rounded off one digit, there would
still be at least ten counts of uncertainty in the last place. He
figured that would give him not only “enough” accuracy, but would
even give him a guard digit for good luck.
Alas, Bob was not lucky. Part of his problem is that he assumed that
roundoff errors would be random and would add in quadrature. In this
case, they aren’t and they don’t. The errors accumulate linearly (not
in quadrature) and cause Bob’s answer to be systematically high. The
offset in the answer in this case is slightly less than the error
bars, but if we had averaged a couple hundred more points the error
would have accumulated to disastrous levels.
Roundoff errors may have a lopsided distribution
even if the raw noise has a nice symmetric Gaussian distribution.
|
|
|
|
Carol was even more unlucky. She rounded off her intermediate results so
that every number on the page reflected its own uncertainty (one count,
possibly more, in the last digit). In this case, her roundoff errors
accumulate in the “down” direction, with spectacularly bad effects.
The three students turned in the following “bottom line” answers:
|
Alice | | Bob | | Carol |
| .00435 ± 0.0018 | | .00442 | | .0034
|
| (34)
|
Note that Alice, Bob, and Carol are all analyzing the same raw data; the
discrepancies between their answers are entirely due to the analysis, not
due to the randomness with which the data was drawn from the ensemble.
Alice obtains the correct result. This is shown by the single black
point with error bars at the top of figure 31. Bob’s
result is slightly worse, but similar. Carol’s result is terrible, as
shown by the red point with error bars at the top of
figure 31.
Take-home message #3: Do not assume that roundoff errors are
random. Do not assume that they add in quadrature. It is waaaay too
easy to run into situations where they accumulate nonrandomly,
introducing a bias into the result. Sometimes the bias is obvious,
sometimes it’s not.
Important note: computer programs6 and hand calculators round off the data at every step.
IEEE 64-bit floating point is slightly better than 15 decimal places,
which is enough for most purposes but not all. Homebrew
numerical integration routines are particularly vulnerable to serious
errors arising from accumulation of roundoff errors.
One of the things that contributes to Bob’s systematic bias can be
traced to the following anomaly: Consider the number 0.448. If we
round it off, all at once, to one decimal place, we get 0.4. On the
other hand, if we round it off in two steps, we get 0.45 (correct to
two places) which we then round off to 0.5. This can be roughly
summarized by saying that the roundoff rules do not have the
associative property. If you have this problem, you might find it
amusing to try the round-to-even rule: round the fives toward
even digits. That is, 0.75 rounds up to 0.8, but 0.65 rounds down to
0.6.
There
are cases where this is imperfect (e.g. 0.454) but it’s better
overall, it’s easy to implement, and it has a pleasing symmetry.
(This rule has been invented and re-invented many times; I re-invented
it myself when I was in high school.) Alas, it is not really an
improvement in any practical sense.
The important point is this: If fiddling with the roundoff rules
produces a non-negligible change in the results, it means you are in
serious trouble. It means the situation is overly burdened by
roundoff errors, and fiddling with the roundoff rules is just
re-arranging deck chairs on the Titanic. Usually the only real
solution is to use more precision (more guard digits) during the
calculation ... or to use a different algorithm, so that fewer steps
(hence fewer roundings) are required. If the rounding is part of a
purely mathematical exercise, keep tacking on guard digits until the
result is no longer sensitive to the details of the roundoff rules.
If the rounding is connected to experimental data, consider
redesigning the experiment so that less rounding is required, perhaps
by nulling out a common-mode signal early in the process. This might
be done using a bridge, or phaselock techniques, or the like.
You can play with the spreadsheet yourself. For fun, see if you can
fiddle the formulas so that Bob’s bias is downward rather than upward.
Save the spreadsheet (reference 16) to disk and open it with
your favorite spreadsheet program.
Notes:
-
I’ve got automatic recalculation turned off; you can either turn
it back on, or push your spreadsheet’s “recalculate” button (F9 or
some such) when necessary.
- Hiding in columns R, S, and T is a Box-Muller transformation to
draw numbers randomly from a Gaussian distribution. You might think
any decent spreadsheet would have a built-in function to generate a
normal distribution, but some versions of Excel don’t. (Sometimes
it’s provided by an add-in.) In any case, it’s good to know the
Box-Muller trick.
Additional constructive suggestions and rules of thumb:
-
Remember, uncertainty is not the same as insignificance.
- It is always safer to have too many digits than too few.
- Suppose you know the Nth digit is uncertain, for
physics-related reasons. Any digits to the right of that are
guard digits. They can’t hurt unless they become unduly
laborious – but now in the era of hand calculators and spreadsheet
programs it’s often easier to carry huge numbers of digits than it is
to figure out exactly how many digits are needed at each step. The
purpose of the guard digits is to ensure that accumulated roundoff
errors remain smaller than the physics-related errors.
- Before you decide to round off, you must do some sort of
theoretical and/or operational check to ensure that rounding doesn’t
introduce a serious error.
- Beware that there are a lot of pseudo-experts and textbooks out
there who have no understanding of signal recovery, and blindly put
complete faith in some “sig digs rules”. Just because they do it
doesn’t make it right.
- If you have something worth saying, don’t say it in terms of
“significant digits”. There are better ways. For instance,
rather than saying “this is good to 5 sig digs”, it would
be better to say “this is accurate to 10 ppm”.
- See also section 8.2, reference 8,
and reference 10.
If you have something worth saying,
don’t say it in terms of “significant figures”.
|
|
|
|
There exist very detailed guidelines for rounding off if that turns out
to be necessary.
-
- a) Here is a crude way to check whether we are carrying enough
guard digits in the intermediate steps. Ask the question: If we did
this twice, rounding up at every step in one case and rounding down at
every step in the other case, would both cases give the same answer,
to an acceptable approximation? If not, we need to carry more
digits.
- b) Here is a more reliable check: Ask the question: If we ran the
calculation N times, randomly rounding up or down at each step in
each run, would every run give the same answer, to an acceptable
approximation? If not, we need to carry more digits.
- c) In the case where the roundoff errors are small, you might be
able to get away with an analytic approach. This involves looking at
the first derivative of the final answer with respect to whatever
quantity you want to round off.
This is risky in a multi-step or iterated calculation where many
roundoff operations occur. That’s because you need to worry about
accumulation of errors.
The main advantage is that if you have a problem and are trying to fix
it, the analytic approach will probably tell you where to focus your
attention. Very commonly, some steps require extra digits while other
steps do not.
7.14 Crank Three Times™
Here’s a simple yet powerful way of estimating the uncertainty of a
result, given the uncertainty of the thing(s) it depends on.
Here’s the procedure, in the simple case when there is only one input
variable with appreciable uncertainty:
- Set up the calculation. Do it once in the usual way, using the
nominal, best-estimate values for all the input variables.
- Then re-do
the calculation with the uncertain variable at the end of its upper error
bar.
- Then re-do the calculation with the uncertain variable at the
end of its lower error
bar.
I call this the Crank Three Times™ method. Here
is an example:
|
| | x | | | | | 1/x |
| === | | | | | === |
| 2.02 | (high case) | | → | | .495 |
| 2 | (nominal case) | | → | | .5 |
| 1.98 | (low case) | | → | | .505 |
|
(35) |
Equation 35 tells us that if x is distributed
according to x = 2±.02 then 1/x is distributed according to 1/x
= .5±.005. Equivalently we can say that if x = 2±1% then 1/x
= .5±1%. We remark in passing that the percentage uncertainty
(aka the relative uncertainty) is the same for x and 1/x,
which is what we expect provided the uncertainty is small.
The Crank Three Times™ method is a type of “what if”
analysis. We can also consider it a simple example of an
iterative numerical method of estimating the uncertainty (in
contrast to the step-by-step first-order methods described in
section 7.20). This simple method is a nice lead-in
to fancier iterative methods such as Monte Carlo, as discussed in
section 7.16.
The Crank Three Times™ method is by no means an exact
error analysis. It is an approximation. The nice thing is that you
can understand the nature of the approximation, and you can see that
better and better results are readily available (for a modest price).
One of the glories of the Crank Three Times™ method is
that in cases where it doesn’t work, it will tell you it isn’t
working, provided you listen to what it’s trying to tell you. If you
get asymmetrical error bars, you need to investigate further.
Something bad is happening, and you need to check closely to see
whether it is a little bit bad or very, very bad.
As far as I can tell, for every flaw that this method has, the
sig-figs method has the same flaw plus others ... which means Crank
Three Times™ is Pareto superior.
This method requires no new software, no learning curve, and no new
concepts beyond the concept of uncertainty itself. In particular,
unlike significant digits, it introduces no wrong concepts.
Crank Three Times™ shouldn’t require more than a few
minutes of labor. Once a problem is set up, turning the crank should
take only a couple of minutes; if it takes longer than that you should
have been doing it on a spreadsheet all along. And if you are using a
spreadsheet, Crank Three Times™ is super-easy and
super-quick.
If you have N variables that are (or might be) making a significant
contribution to the uncertainty of the result, the Crank Three
Times™ method could more precisely be called the Crank
2N+1 Times™ method. Here’s the procedure: Set up the
spreadsheet and wiggle each variable in turn, and see what happens.
Wiggle them one at a time, leaving the other N−1 at their
original, nominal values.
If you are worried about what happens when two of the input variables
are simultaneously at the ends of their error bars, you can check that
case if you want. However, beware that if there are many variables,
checking all the possibilities is exponentially laborious.
Furthermore, it is improbable that many variables would simultaneously
take on extreme values, and checking extreme cases can lead you to
overestimate the uncertainty. For these reasons, and others, if you
have numerous variables and need to study the system properly, at some
point you need to give up on the Crank Three Times™
method and do a full-blown Monte Carlo analysis.
In the rare situation where you want a worst-case analysis, you
can move each variable to whichever end of its error bar makes
a positive contribution to the final answer, and then flip
them all so that each one makes a negative contribution.
In most cases, however, a worst-case analysis is wildly
over-pessimistic, especially when there are more than
a few uncertain variables.
Remember: there are many cases, especially when there are multiple
uncertain variables and/or correlations among the variables and/or
nonlinearities, your only reasonable option is Monte Carlo, as
discussed in section 7.16. The Crank Three
Times™ method can be considered an ultra-simplified
variation of the Monte Carlo method, suitable for introductory
reconnaissance.
Here is another example, which is more interesting because it
exhibits nonlinearity:
|
| | x | | | | | 1/x |
| === | | | | | === |
| 2.9 | (high case) | | → | | .34 |
| 2 | (nominal case) | | → | | .5 |
| 1.1 | (low case) | | → | | .91 |
|
(36) |
Equation 36 tells us that if x is distributed
according to x = 2±.9 then 1/x is distributed according to 1/x
= .5(+.41−.16). Equivalently we can say that if x = 2±45% then
1/x = .5(+82%−31%). Even though the error
bars on x are symmetric, the error bars on 1/x are markedly
lopsided.
Lopsided error bars are fairly common in practice. Sometimes
they are merely a symptom of a harmless nonlinearity,
but sometimes they are a symptom of something much worse,
such as a singularity or a branch cut in the
calculation you are doing.
This is vastly superior to the step-by-step first-order methods
discussed in section 7.20, which blissfully
assume everything is linear. That is to say, in effect they
expand everything in a Taylor series, and keep only the zeroth-order
and first-order terms. In cases where this is not a good
approximation, you are likely to get wrong answers with little or no
warning.
Here is yet another example, which is interesting because it shows how
to handle correlated uncertainties in simple cases. The task is
to calculate the molar mass of natural bromine, given the nuclide mass
for each isotope, and the corresponding natural abundance.
The trick here is to realize that the abundances must add up to 100%.
So if one isotope is at the low end of its error bar, the other
isotope must be at the high end of its error bar. So the abundance
numbers are anticorrelated. This is an example of a sum
rule. For more about correlations and how to handle them, see
section 7.16.
(The uncertainties in the mass of each nuclide are negligible.)
| | | nuclide mass | | | | natural | | | | light case | | nominal case | | heavy case | |
| | | / dalton | | | | abundance | | | |
| 79Br | | 78.9183376(20) | | × | | 50.686+.026% | | = | | 40.02107 | | | | | | more |
| 79Br | | 78.9183376(20) | | × | | 50.686% | | = | | | | 40.00055 | | | | nominal |
| 79Br | | 78.9183376(20) | | × | | 50.686-.026% | | = | | | | | | 39.98003 | | less |
| 81Br | | 80.9162911(30) | | × | | 49.314+.026% | | = | | | | | | 39.92410 | | more |
| 81Br | | 80.9162911(30) | | × | | 49.314% | | = | | | | 39.90306 | | | | nominal |
| 81Br | | 80.9162911(30) | | × | | 49.314-.026% | | = | | 39.88202 | | | | | | less |
| | | | | | | | | | | ——— | | ——— | | ——— | |
| | | | | | | | | | | 79.90309 | | 79.90361 | | 79.90412 | |
|
So by comparing the three columns (light case, nominal case, and heavy
case), we find the bottom-line answer: The computed molar mass of
natural bromine is 79.90361(52). This is the right answer based on a
particular sample of natural bromine. The usual “textbook” value is
usually quoted as 79.904(1), which has nearly twice as much
uncertainty, in order to account for sample-to-sample variability.
Note that if you tried to carry out this calculation using
“significant figures” you would get the uncertainty wrong.
Spectacularly wrong. Off by two orders of magnitude. The relative
uncertainty in the molar mass is two orders of magnitude smaller than
the relative uncertainty in the abundances.
7.15 Another Example: Magnesium Mass, Preliminary Attempt
This is based on question 3:21 on page 122 of reference 17.
Suppose we want to calculate (as accurately as possible) the molar
mass of natural magnesium, given the mass of the various isotopes and
their natural abundances.
Many older works referred to this as the atomic mass, or (better)
the average atomic mass ... but the term molar mass is strongly
preferred. For details, see reference 18.
The textbook provides the raw data shown in table 7.
|
isotope | molar mass / dalton | abundance |
|
| 24Mg | 23.9850 | 78.99% |
| 25Mg | 24.9858 | 10.00% |
| 26Mg | 25.9826 | 11.01% |
Table 7: Isotopes of Magnesium, Rough Raw Data
The textbook claims that the answer is 24.31 dalton and that no greater
accuracy is possible. However, we can get a vastly more accurate result.
The approach in the textbook has multiple problems:
-
The textbook uses methods that vastly overestimate the halfwidth
of the distribution. This damages the estimated uncertainty.
- The textbook fails to take into account the fact that the
abundance variables are highly correlated, as they must be, since they
always sum to 100%. This further damages the estimated uncertainty.
- The textbook expresses the uncertainty using the dreaded “sig
digs” rules, which give only a crude indication of the halfwidth of
the distribution. This does yet more damage to the estimated
uncertainty.
- The textbook rounds off the answer according to the usual
foolish “sig digs” rules, which don’t permit guard digits. The
roundoff error damages the nominal value.
It is tempting to blame all the problems on the “sig digs” notation,
but that wouldn’t be fair in this case. The primary problem is
mis-accounting for the uncertainty, and as we shall see, we are still
vulnerable to mis-accounting even if the uncertainty is expressed
using proper notation.
Similarly note that even if we did manage to get good estimate of the
uncertainty, the “sig digs” rules would not have called for such
drastic rounding. So the propagation-of-error issues really are
primary.
Let’s make a preliminary attempt to figure out what’s going on. If we
clean up the notation, it will facilitate understanding and
communication. In particular, it will expose a bunch of problems that
the text sweeps under the rug.
We can start by re-expressing the textbook data so as to make the
uncertainties explicit. We immediately run into some unanswerable
questions, because the “sig digs” notation in table 7
gives us only the crudest idea of the uncertainty ... is it half a
count in the last decimal place? Or one count? Or more??? If we use
only the numbers presented in the textbook, we have to guess. Let’s
temporarily hypothesize a middle-of-the-road value, namely three
counts of uncertainty in the last decimal place. We can express this
in proper notation, as shown in table 8.
|
isotope | molar mass / dalton | abundance |
|
| 24Mg | 23.9850(3) | 78.99(3)% |
| 25Mg | 24.9858(3) | 10.00(3)% |
| 26Mg | 25.9826(3) | 11.01(3)% |
Table 8: Isotopes of Magnesium, Rough Data with Explicit Uncertainty
This gives the molar mass of the 25Mg isotope with a relative accuracy
of 12 parts per million (12 ppm), while the abundance is given with a
relative accuracy of 3 parts per thousand (3000 ppm). So in some
sense, the abundance number is 250 times less accurate.
If you think about the data, you soon realize that the abunance
numbers are in percentages, and must add up to 100%. We say
there is a sum rule.
The sum rule means the uncertainty in any one of the abundance numbers
is strongly anticorrelated with the uncertainty in the other two. The
widely-taught pseuo-sophisticated “propagation of uncertainty” rules
don’t take this into account; instead, they rashly assume that all
errors are uncorrelated. If you just add up the abundance numbers
without realizing they are percentages, i.e. without any sum rule,
you get
|
78.99(3) + 10.00(3) + 11.01(3) = 100.00(5) ???
(37) |
with (allegedly) 500 ppm uncertainty, even though the sum rule tells
us they actually add up to 100 with essentially no uncertainty:
|
78.99(3) + 10.00(3) + 11.01(3) = 100.0±0
(38) |
Even if you imagine that equation 38 is not perfectly
exact – perhaps because it fails to account for some fourth,
hitherto-unknown isotope – the sum must still be very nearly 100%,
with vastly less uncertainty than equation 37 would
suggest.
To say the same thing another way, we are talking about three numbers
(the percent abundance of the three isotopes). Taken together, these
numbers specify a point in some abstract three-dimensional space.
However, the valid, physically-significant points are restricted to a
two-dimensional subspace (because of the sum rule).
Here’s another fact worth noticing: All three isotope masses are in
the same ballpark. That means that uncertainties in the abundance
numbers will have little effect on the sought-after average mass.
Imagine what would happen if all three isotopes had the same identical
mass. Then the percentages wouldn’t matter at all; we would know the
average mass with 12 ppm accuracy, no matter how inaccurate the
percentages were.
There are various ways to take the “ballpark” property into account.
One method, as pointed out by Matt Sanders, is to subtract off the
common-mode contribution by artfully regrouping the terms in the
calculation. That is, you can subtract 25 (exactly) from each of the
masses in table 8, then take the weighted average of what’s left
in the usual way, and then add 25 (exactly) to the result. The
differences in mass are on the order of unity, i.e. 25 times smaller
than the masses themselves, so this trick makes us 25 times less
sensitive to problems with the percentages. We are still
mis-accounting for the correlated uncertainties in the percentages,
but the mis-accounting does 25 times less damage.
The idea of subtracting off the common-mode contribution is a good
one, and has many applications. The idea was applied here to a
mathematical calculation, but it also applies to the design of
experimental apparatus: for best accuracy, make a differential
measurement or a null measurement whenever you can.
To summarize, subtracting off the common-mode contribution is a good
trick, but (a) it requires understanding the problem and being
somewhat devious, (b) in its simplest form, it only works if the
problem is linear, (c) it doesn’t entirely solve the problem, because
it doesn’t fully exploit the sum rule.
7.16 Magnesium Mass, Monte Carlo Solution
The situation described in section 7.15 has so many
problems that we need to start over.
For one thing, if we’re going to go to the trouble of calculating
things carefully, we might as well use the best available data (rather
than the crummy data given in the textbook, i.e. table 8). A
secondary source containing mass and abundance data for the isotopes
of various elements can be found in reference 19. We can use
that for our mass data. Another secondary source is reference 20.
| isotope | molar mass / dalton | |
|
| 24Mg | 23.9850423(8) |
| 25Mg | 24.9858374(8) |
| 26Mg | 25.9825937(8) |
Table 9: Isotopes of Magnesium, IUPAC Mass Data
Reference 19 appears to be taking its magnesium abundances from
reference 21, and it is always good to look at the primary
sources if possible, so let’s do that.
| | | abundance |
| isotope pair | | ratio | | 95% confidence |
|
| 25Mg/24Mg | | x = 0.12663 | ± | 0.00013 |
| 26Mg/24Mg | | y = 0.13932 | ± | 0.00026
|
Table 10: Isotopes of Magnesium, NBS Abundance Data
The first thing you notice is that that the scientists to did the work
report their results in the form 0.12663 ± 0.00013 at 95%
confidence. The uncertainty is clearly and explicitly stated. People
who care about their data don’t use sig figs. (Beware that the 95%
error bar is two standard deviations, not one.)
Another thing you notice is that they report only two numbers for the
abundance data. They report the ratio of 25Mg abundance to
24Mg abundance, and the ratio of 26Mg abundance to
24Mg abundance. They report the uncertainty for each of these
ratios. These two numbers are just what we need to span the
two-dimensional subspace mentioned in section 7.15. The
authors leave it up to you to infer the third abundance number (by
means of the sum rule). Similarly they leave it up to you to infer
the uncertainty of the third number ... including its correlations.
The correlations are important, as we shall see.
To find the percentages in terms of the ratios (x and y) as defined
in table 10, we can use the following formulas:
|
24Mg fraction | | = | | |
| 25Mg fraction | | = | | |
| 26Mg fraction | | = | | |
| (39)
|
You can easily verify that the abundances add up to exactly 100%,
and that the ratios are exactly x and y, as they should be.
The smart way to deal with this data, including the correlations, is
to use the Monte Carlo technique. As we shall see, this is
simultaneously easier and more powerful than the textbook approach.
Monte Carlo has many advantages. It is a very general and very
powerful technique. It can be applied to nonlinear problems. It is
flexible enough to allow us to exploit the sum rule directly.
Relatively little deviousness is required.
As mentioned in section 1.2 and section 5, we
must keep in mind that there is no such thing as an “uncertain
quantity”. There is no such thing as a “random number”. Instead
we should be talking about probability distributions. There are many
ways of representing a probability distribution. We could represent
it parametrically (specifying the center and standard deviation). Or
we could represent it graphically. Or (!) we could represent it by a
huge sample, i.e. a huge ensemble of observations drawn from the
distribution.
The representation in terms of a huge sample is sometimes considered
an inelegant, brute-force technique, to be used when you don’t
understand the problem ... but sometimes brute force has an
elegance all its own. Doing this problem analytically requires a
great deal of sophistication (calculus, statistics and all that) and
even then it’s laborious and error-prone. The Monte Carlo approach
just requires knowing one or two simple tricks, and then the computer
does all the work.
You can download the spreadsheet for solving the Mg molar mass question.
See reference 22.
The strategy goes like this: As always, whenever we see an expression
of the form A±B we interpret it as a probability distribution.
We start by applying this rule to the mass data in table 9
and the abundance-ratio data in table 10. This gives a
mathematical distribution over five variables. Then we represent this
distribution by 100 rows of simulated observations, with five
variables on each row, all randomly and independently drawn from the
mathematical distribution. This gives us another representation of
the same distribution, namely a sampled representation. Using these
observations, on each row we we make an independent trial calculation
of the average mass, and then compute the mean and standard deviation
of these 100 trial values.
On each row of the spreadsheet, the five raw observations are drawn
independently. The three percentage abundance numbers are not raw
data, but instead are calculated from the two abundance ratios. The
means the three percentage abundance numbers are not independent.
They exhibit nontrivial correlations.
The final answer appears in cells M10 and M12, namely 24.30498(18),
where our reported uncertainty represents the one-sigma error bar
(unlike reference 21, which reported the two-sigma error
bar).
Technical notes:
-
In the spreadsheet, I have the “automatic recalculation”
feature turned off. You can re-run the calculation – using a new set
of random numbers – by hitting the F9 button.
- Once again Box-Muller transforms are used to generate a sample
of a Gaussian normal distribution. This is implemented by columns O
through Z of the spreadsheet. You are not expected to remember the
details of this trick ... but you should remember that it exists, and
can google Box-Muller to find out the details whenever you need a
supply of normally-distributed numbers.
If you compare my value for the average mass against the value quoted
in reference 21, you find that the nominal value is the same,
but the estimated uncertainty is slightly less. There are a couple of
explanations for this. For one thing, they make an effort to account
for some systematic biases that the Monte Carlo calculation knows
nothing about. Also, at one point they add some uncertainties
linearly, whereas I suspect they should have added them in quadrature.
Futhermore, it’s not clear to what extent they accounted for
correlated uncertainties.
7.17 Exercise
Pretend that we didn’t have a sum rule. That is, pretend that the
abundance data consisted of three independent random variables,
with standard deviations as given in table 8. Modify the
spreadsheet accordingly. Observe what happens to the nominal value
and the uncertainty of the answer. How important is the sum rule?
Hint: There’s an entire column of independent Gaussian random numbers
lying around unused in the spreadsheet.
7.17.1 Discussion: Mg Mass
To summarize: As mentioned near the top of section 7.15,
the textbook approach has multiple problems: For one thing, it does
the propagation-of-uncertainty calculations without taking the sum
rule into account (which is a huge source of error). Then the dreaded
“sig digs” rules make things worse in two ways: they compel the
non-use of guard digits, and they express the uncertainty very
imprecisely.
The textbook answer is 24.31 dalton, with whatever degree of uncertainty is
implied by that number of “sig digs”.
We now compare that with the our preferred answer, 24.30498(18)
dalton. Our standard deviation is less than 8 ppm; theirs is
something like one part per thousand (although we can’t be sure). In
any case, their uncertainty is more than 100 times worse than ours.
Their nominal value differs from our nominal value by something like
27 times the length of our error bars. That’s a lot.
Last but not least, note that this whole calculation should not be
taken overly seriously. The high-precision abundance-ratio data we
have been using refers to a particular sample of magnesium. Magnesium
from other sources can be expected to have a different isotope ratio,
well outside the error bars of our calculation.
7.18 Reporting Correlated Uncertainties
In this section, we are interested in the isotope abundance
percentages (not just the average molar mass).
Recall that reference 21 reported only the two abundance
ratios. In contrast, the text reported three abundance percentages,
without mentioning the sum rule, let alone explaining how the sum rule
should be enforced. So the question arises, if we wanted to report
the three abundance percentages, what would be the proper way to do
it?
The first step toward a reasonable representation of correlated
uncertainties is the covariance matrix. This is shown in cells
Q3:S5 in the spreadsheet (reference 22), and shown again in
equation 40
|
covariance | | = | | ⎡
⎢
⎢
⎣ | | 9.255 | | −1.080 | | −8.175 |
| −1.080 | | 2.307 | | −1.227 |
| −8.175 | | −1.227 | | 9.402 |
| ⎤
⎥
⎥
⎦ | × 10−9
|
|
| (40)
|
For uncorrelated variables, the off-diagonal elements of the
covariance matrix are zero. Looking at the matrix in our example we
see that the off-diagonal elements are nonzero, so we know there are
correlations. Of course we knew that already, because the sum rule
guarantees there will be correlations.
Alas, it is not easy to understand the physical significance of a
matrix by looking at its matrix elements. For example, it may not be
obvious that the matrix in equation 40 is singular
... but if you try to invert it, you’re going to have trouble.
Ideally, if we could represent the matrix in terms of its singular
value decomposition (SVD), its meaning would become considerably
clearer. Since the matrix is symmetric, the SVD is identical to the
eigenvalue decomposition (EVD).
There exist software packages for calculating the SVD. If the matrix
is larger than 3×3, it is generally not practical to calculate
the SVD by hand.
- For 2×2, find the large eigenvectors by applying
the power method. Find the small eigenvector by applying
the power method to the inverse matrix.
- For 3×3, find the large and small eigenvectors using the
power method, as above. Then find the third eigenvector by taking a
cross product. (A spreadsheet formula for calculating the cross
product can be found in reference 23.)
Once you have the eigenvectors, it is trivial to get the eigenvalues.
Even in situations where you cannot readily obtain the exact SVD, you
can still make quite a lot of progress by using an approximate SVD,
which I call a ballpark decomposition (BPD). This is shown in cells
Q9:AA11 in the spreadsheet and shown again in equation 41.
|
covariance | | = | | R S R† |
| | | = | | | | ⎡
⎢
⎢
⎣ | | 0.707 | | 0.408 | | 0.577 |
| 0.000 | | −0.816 | | 0.577 |
| −0.707 | | 0.408 | | 0.577 |
| ⎤
⎥
⎥
⎦ |
| ⎡
⎢
⎢
⎣ | | 17.503 | | −0.128 | | 0.000 |
| −0.128 | | 3.460 | | 0.000 |
| 0.000 | | 0.000 | | 0.000 |
| ⎤
⎥
⎥
⎦ |
| ⎡
⎢
⎢
⎣ | | 0.707 | | 0.000 | | −0.707 |
| 0.408 | | −0.816 | | 0.408 |
| 0.577 | | 0.577 | | 0.577 |
| ⎤
⎥
⎥
⎦ |
|
| (41)
|
where R is a unitary matrix and S is “almost” diagonal.
Specifically, R consists of a set of approximate eigenvectors of the
covariance matrix, considered as column vectors, normalized and
stacked side-by-side. The approximate eigenvalues of the covariance
matrix appear on the diagonal of S.
The approximate eigenvalues can be figured out using the following
reasoning: It is a good guess that [1, 1, 1] or something close to
that is the most-expensive eigenvalue of the covariance matrix,
because if you increase all three abundance percentages, you violate
the sum rule. Secondly, if you check this guess against the computed
covariance matrix, equation 40, it checks out, in the
sense that it is an eigenvector with zero eigenvalue. Thirdly, if you
look at the definition of the covariance matrix and apply a little
algebra, you can prove that [1, 1, 1] is exactly (not just
approximately) an eigenvector with zero eigenvalue.
Meanwhile, the cheapest eigenvector must be [1, 0, −1] or something
like that, because that corresponds to increasing the amount of
24Mg and decreasing the amount of 26Mg, which is cheap (in
terms of Mahalanobis distance) because of the relatively long error
bar on the 26Mg/24Mg ratio as given in table 10.
The third approximate eigenvector is determined by the requirement
that it be perpendicular to the other two. (You might guess that it
would be something like [1, −1, 0], but that wouldn’t be
perpendicular.) In general, you can take a guess and then
orthogonalize it using the Gram-Schmidt process. In the particular
case of D dimensions where D−1 of the vectors are known, you can
take the cross product (or its higher-dimensional generalization). In
the present example, the third member of the orthogonal set is [1,
−2, 1]. This is middle eigenvector, neither the cheapest nor the
most expensive.
We interpret this as follows: Since the off-diagonal elements in the
S-matrix in equation 41 are relatively small, we can say
that the uncertainties in the eigenvalues are almost uncorrelated.
The eigenvalues are a good (albeit not quite exact) indication of the
variance associated with the corresponding eigenvector. Take the
square root of the variance to find the standard deviation.
For what it’s worth, equation 42 gives the actual SVD. You
can see that it is not very different from the ballpark decomposition
in equation 41.
|
covariance | | = | | R S R† |
| | | = | | | | ⎡
⎢
⎢
⎣ | | −0.703 | | 0.415 | | 0.577 |
| −0.007 | | −0.816 | | 0.577 |
| 0.711 | | 0.402 | | 0.577 |
| ⎤
⎥
⎥
⎦ |
| ⎡
⎢
⎢
⎣ | | 17.505 | | 0 | | 0.000 |
| 0 | | 3.459 | | 0.000 |
| 0.000 | | 0.000 | | 0.000 |
| ⎤
⎥
⎥
⎦ |
| ⎡
⎢
⎢
⎣ | | −0.703 | | −0.007 | | 0.711 |
| 0.415 | | −0.816 | | 0.402 |
| −0.577 | | −0.577 | | −0.577 |
| ⎤
⎥
⎥
⎦ |
|
| (42)
|
In C++ the armadillo package can be used to perform SVD. In
python the numpy package knows how to do SVD.
7.19 Another Example: Solving a Quadratic via Monte Carlo
Consider the following scenario. Suppose
we are given that:
|
| | a x2 + b x + c | = | 0 | |
| a | = | 1 | | exactly |
| b | = | 2.08 | ± 1.0 | Gaussian, IID |
| c | = | 1.08 | ± 0.05 | Gaussian, IID |
|
(43) |
The variable x behaves as if it were drawn from some distribution
X, and our goal is to find a description of this distribution.
It suffices to treat this as a mathematical puzzle unto itself, but if
you would prefer to have some physical interpretation, context, and
motivation, we remark that equations like this (and even nastier
equations) arise in connection with:
- trajectory of a particle subject to uniform acceleration;
- wave propagation (reflected wave, transmitted wave);
- optimization problems (finding the shortest path);
- finding pH as a function of concentration;
- et cetera.
We can solve this equation using the smart version of the quadratic
formula, as explained in reference 14.
We can get a feel for the two variable coefficients (b and c) by
making a two dimensional scatter plot. The result is a sample drawn
from a two-dimensional Gaussian distribution, as shown in
figure 32.
 Figure 32
Figure 32: Coefficient b versus Coefficient
c
The two-dimensional Gaussian distribution from which this sample was
drawn has the following properties: The probability density is highest
near the nominal value of (b, c) = (−2.08, 1.08). The density tails
off from there, gradually at first and then more quickly.
Let’s see what we can learn by using the Crank Three
Times™ method. In this case it will actually require
five turns of the crank, since we have two uncertain coefficients to
deal with.
The first crank, as always, involves setting the coefficients a,
b, and c to their nominal values and solving for x. When we do
this, we find two solutions, namely x=1.00 and x=1.08. In some
sense these x values are “centered” on the point x=1.04. We
shall see that x=1.04 is a point of pseudo-symmetry for this system,
and we shall call it the “nominal” x-value.
In figure 32 the region with the tan background
corresponds to points (b, c)-space where the discriminant b2−4ac
is positive, resulting in a pair of real-valued solutions for x.
Meanwhile, the region with the gray background corresponds to points
where the discriminant is negative, resulting in a conjugate pair of
complex-valued solutions.
There is zero probability of a point falling
exactly on the boundary. This would result in a double root.
For example, the point (b, c) = (−2.08, 1.0816) would
produce a double root at x=1.04. Since this is vanishingly
unlikely, we will have nothing further to say about it, and
will speak of the roots as occurring in pairs.
For present purposes, we will keep all the x-values we find,
including both elements of each pair of roots, and including
complex as well as real values. (In some
situations there could be additional information that would
allow us to discard some of the solutions as unphysical,
but for now it is easier and more informative to consider
the most general case, and just keep all the solutions.)
If we (temporarily!) consider just the real-valued solutions, we find
that x has lopsided error bars. This means it is not safe to
describe the x-distribution in terms of some nominal value
plus-or-minus some uncertainty. Lopsided error bars are a warning,
telling us to investigate more closely, to see whether the problem is
just a mild nonlinearity, or whether something very very bad is going
on.
When we take into account the complex-valued solutions, we immediately
discover that the situation falls into the very very bad category.
The Crank Three Times™ method has given us a valuable
warning, telling us that it cannot give us the full picture. To get
the full picture, we need to do a full-blown Monte Carlo analysis.
The result of such an analysis can be presented as a scatter plot in
the complex plane, as shown in figure 33.
 Figure 33
Figure 33: Pitchfork :
x-values for Δ
b=1.0, Δ
c=0.05
The distribution of x-values can be plotted in the complex plane, as
shown in figure 33. This distribution does not even
remotely resemble a two-dimensional Gaussian. It looks more like some
sort of diabolical pitchfork.
The probability density actually goes to zero at the nominal point
x=1.04.
Sprouting out from the nominal x-value are four segments, shown
using four different colors in the diagram. These correspond to
whether we take the plus or minus sign in front of the ± square
root, and whether the discriminant (b2−4ac) is positive or
negative. (The sign of the discriminant depends on the luck of the
draw, when we draw values for the coefficients b and c.
The ± sign does not depend on the luck of the draw,
because except in the case of a double root, for every point
in (a,b,c)-space we get two points in x-space.)
This diagram is more-or-less equivalent to something that
in another context would be called a root locus plot
or root locus diagram.
In the interests of simplicity, let us consider a slightly different
version of the same problem. The statement of the problem is the same
as before, except that there is less uncertainty on the coefficients.
Specifically, we wish to describe the distribution X that models the
behavior of the variable x, given that:
|
| | a x2 + b x + c | = | 0 | |
| a | = | 1 | | exactly |
| b | = | 2.08 | ± 0.01 | Gaussian, IID |
| c | = | 1.08 | ± 0.01 | Gaussian, IID |
|
(45) |
The scatter plot for the coefficients (b, c) is shown
in figure 34.
 Figure 34
Figure 34: Coefficient b versus Coefficient
c
The corresponding scatter plot for the solutions x in the complex
plane is shown in figure 35. The pitchfork shape is
less evident here. It looks more like a Greek cross. The curvature
of the upper and lower segments is barely visible. Compared to
figure 33, this is similar except more “zoomed in”;
that is, all the points now lie closer to the nominal x-value. The
probability density is still zero at the nominal point, so the nominal
solution is by no means the best solution. It is arguably not even a
solution at all.
Mathematically speaking, it is straightforward to calculate the sample
mean, i.e. the mean of the points shown in
figure 35. It comes out to very nearly the nominal
x-value, namely x=1.04.
Also mathematically speaking, it is straightforward to calculate
the variance and the standard deviation of the sample points.
The standard deviation is essentially the RMS distance of
the points from the mean value. Actually I prefer to call
it the RMAS, for root-mean-absolute-square, since technically
speaking we want the absolute square |x|2 rather than
the plain old square x2. It comes out to be about 0.11
for this sample.
I emphasize that calculating these numbers is easier than assigning
any useful meaning to the numbers. Specifically, it would be grossly
misleading to describe this distribution in terms of its mean and
standard deviation. That is, it would be grossly misleading to write
x=1.04±0.11 without stating the form of the distribution. This
distribution is about as non-Gaussian as anything I can imagine. For
figure 35, it might make sense to describe the mean
and standard deviation of each of the four segments separately ... but
for figure 33, not even that would do a good job of
describing the overall x-distribution.
Note that if we – hypothetically and temporarily – pretend the RMAS
is a useful measure of the uncertainty, then the relative uncertainty on
x is almost 11 percent, which is more than an order of magnitude
larger than the uncertainty in either of the coefficients.
Non-hypothetically speaking, keep in mind that the RMAS barely begins
to describe what we know (and don’t know) about the distribution
of x-values.
These examples illustrate the importance of plotting the data and
looking at it, rather than relying on mathematical abstractions such
as mean and standard deviation. If you just blithely calculated
numerical values for the mean and standard deviation, you would come
nowhere near understanding this system.
These examples also illustrate the tremendous power of the Monte Carlo
method. It works when other methods fail.
- For the scenario given in equation 45 the Crank Three
Times™ method fails. It fails gracefully, in the sense
that when you try it, you get very peculiar results, including complex
numbers, so you know you that three cranks will be nowhere near
sufficient. You need many, many cranks, i.e. a full-blown Monte
Carlo.
- The step-by-step first-order propagation approach described in
section 7.20 also fails. It is guaranteed to fail,
and extending it to second order (or higher order) won’t help. That’s
because the square-root function is not differentiable at any point
where its argument goes to zero, i.e. for any point along the tan/gray
boundary in figure 34. This guarantees we will have
trouble constructing a Taylor series. If we pick any point in the
(b, c) plane and construct a Taylor series there, the radius of
convergence cannot extend across the tan/gray boundary. Therefore
neither the nominal point nor any other point in the plane will give
us a radius of converence large enough to encompass all the points in
the sample. It should be obvious that there is no circle that
encompasses all the points without crossing the tan/gray boundary,
since the points themselves sit on both sides of the boundary.
In the introductory texts, when they lay down “rules” for
propagating the uncertainty step-by-step, they often neglect to
mention that you need to systematically check the radius of
convergence at every step. If you fail to check, convergence problems
will go unnoticed, and you will get seriously wrong answers.
Unfortunately, this sort of checking is quite laborious, so it is
seldom done, and serious errors are common.
Remember that there are three problems layered on top of each other:
Misrepresentation, Malexpansion, and Correlation. This is discussed
in section 7.1.
Bottom line: In this example, and in many similar examples, if you
want a good, simple, quantitative answer for the nominal value and
uncertainty of the distribution X, you’re out of luck. There is no
such thing. We need to ask a different question, such as “How can we
understand what’s going on in this system?”
Looking at a scatter plot such as figure 35 is
a good starting point for understanding what is going on.
7.20 Step-by-Step First-Order Propagation of Uncertainty
Suppose we have a procedure, consisting of one or more steps. We
start with ai and then calculate bi and then ci et cetera.
Here ai is an observation drawn from some distribution A. We
assume the distribution A can be represented by a blob of the form
⟨A⟩±[A] where ⟨A⟩ is the mean and
[A] is the standard deviation.
The hallmark of step-by-step propagation is that at each step in the
calculation, rather than keeping track of plain old numbers such as
ai, bi et cetera, we keep track of the corresponding
distributions, by means of the blobs ⟨A⟩±[A],
⟨B⟩±[B], et cetera.
This approach suffers from three categories of problems, namely
misrepresentation, malexpansion, and correlation.
People often ask for some mathematical rules for keeping track of the
uncertainty at each step in a long calculation, literally
“propagating’ the uncertainty on a step-by-step basis. This approach
works fine in a few simple, ideal cases. Perhaps the biggest
advantage of the step-by-step approach is that thinking about the
logic behind the rules helps give you a feel for what’s going on, and
allows you to predict which steps are likely to make the largest
contributions to the overall uncertainty.
On the other hand, beware: The step-by-step
first-order approach is subject to many provisos that often make it
inapplicable to practical problems. (If you ignore the provisos,
you will get wrong answers – often with little or no warning.)In a complicated multi-step problem, you may find that step-by-step
first-order propagation works fine everywhere except for one
or two steps. Alas, a chain is only as strong as its weakest link,
so the method fails to solve the overall problem. The quadratic
formula in section 7.19 serves as an example of just such
an overall failure, even though the method worked for every step
except one, i.e. except for the step that called for extracting the
square root.
Also beware that even in cases where the step-by-step method is
applicable, it can become quite laborious. For example, when
stepping through the quadratic formula (as in equation 43 for example), there is a product, then a sum,
then a square root, then another sum, and then a division. This
requires repeated conversion between absolute uncertainty and
relative uncertainty. In this case, calculating the uncertainty
requires about three times as many arithmetical operations as
calculating the nominal value. You can reduce the workload by using
ultra-crude approximations to the uncertainty (such as sig figs),
but this gives you the wrong answer. There is no advantage to
having an easy way of getting the wrong answer.
Generally speaking, when dealing with messy, complicated, practical
cases you’re better off letting a computer do the work for you. You
can start with the Crank Three Times™ method
discussed in section 7.14, and if that’s not good enough, you
can use the Monte Carlo7 method as discussed in section 7.16.
7.20.2 Step-by-Step Propagation Rules
These rules have some advantage and disadvantages. In situations
where they are valid, they are very convenient. For example, if you
know that a certain distribution has a mean of 19 and a relative
uncertainty of 10%, then if you double every element of the ensemble
you get a new distribution with a mean of 38 and the same relative
uncertainty, namely 10%. This is easy and intuitive, and gets the
right answer in this situation. You don’t need to understand any
calculus, you don’t need to worry about the radius of convergence, and
you hardly need to do any work at all.
However, beware that a collection of anecdotes is not a proof. These
rules work in certain selected situations, but they fail miserably in
other situations.
I assume you already know how to add, subtract, multiply, and divide
numbers, so we will now discuss how to add, subtract, multiply,
and divide probability distributions, subject to certain
restrictions.
Each of the capital-letter quantities here (A, B, and C) is
a probability distribution. We can write A := mA±σA,
where mA is the mean and σA is the standard deviation.
The best way to explain where these rules come from is to use
calculus, but if you don’t know calculus you can (a) start by
accepting the rules as plausible hypotheses, and then (b) checking
them for consistency. More specifically, calculus is needed for any
serious understanding of the limitations of the rules.
- Addition and Subtraction: If you are calculating C := A + B or
C := A − B, provided that A and B are uncorrelated, then the
absolute uncertainties add in quadrature. That is:
- Multiplication and Division: If you are calculating C := A
× B or C := A / B, provided that A and
B are uncorrelated, and provided the
relative uncertainties are small (compared to unity), then the
relative uncertainties add in quadrature. That is:
|
(σC/mC)2 = (σA/mA)2 + (σB/mB)2
(47) |
- Powers: If you are calculating B := AN, provided N is an
exact integer, and provided that A has only a small relative
uncertainty, then the relative uncertainty grows in proportion to N.
That is:
Note that you cannot get this result by applying the product rule.
The product rule is not applicable, since taking powers involves
multiplying quantities with correlated uncertainties.
If N is not an integer, equation 48 is not
reliable. It might work, or it might not. For example, consider the
case where N=½. Suppose we know x2 = y and the distribution
on y is 81±1ppm. The problem is, we don’t know whether
x ≈ 9 or x ≈ −9, so we might need to write x =
0±9, in which case the uncertainty on x is incomparably more than
the uncertainty on y. For more on this, see section 7.19.
- Functions and other operations: The general rule, roughly
speaking, is to expand the function in a first-order Taylor series,
and then apply the first rule above, i.e. the “addition” rule. This
assumes that the function be well approximated by a first-order Taylor
series, which is sometimes a very bad assumption. As an illustration,
suppose you want to calculate the tangent of 89±2 degrees. The
uncertainty in the result is for all practical purposes infinite, far
in excess of what the first-order approximation would have you
believe. You could imagine trying to improve the results by using a
higher-order Taylor series, but (a) that’s laborious, and (b) it
doesn’t fully solve the underlying problem, because the Taylor series
might not converge at all. Sometimes you can figure out the radius of
convergence of the Taylor series – as we do for instance in section 7.19 – but oftentimes it’s much easier to give up on the
step-by-step approach entirely, and just do the Monte Carlo.
7.20.3 More Disclaimers
-
There are a lot of provisos in the rules in section 7.20.2. The provisos must be taken seriously.
Otherwise you may seriously underestimate or overestimate the
uncertainty.
- Please remember that the rules in section 7.20.2
are not sig-figs rules. They are not round-off rules. They allow you
to calculate the standard deviation σA ... but knowing
σA does not oblige you to round off mA to any
particular number of digits. The guidelines for rounding off are
given in section 8.2.
- The step-by-step approach is very laborious. It requires extra
work – fussy, sophisticated work – at every step in the calculation.
This stands in contrast to the Crank Three Times™
approach and the Monte Carlo approach, where all you need to worry
about are the top-line inputs and the bottom-line outputs (unless
there are correlations or other complications). All the intermediate
steps are taken care of by the computer, and you can calculate the
uncertainties using the same program that you were already using for
calculating the nominal values.
- Despite all the limitations, the step-by-step propagation
approach can sometimes be made to work. Thinking about the logic
behind the rules helps give you a feel for what’s going on, and allows
you to predict which steps are likely to make the largest
contributions to the overall uncertainty. This in turn may suggest
ways of redesigning the whole experiment, so as to make it less
sensitive to noise.
Bottom line: As a practical matter, step-by-step “algebraic”
propagation of uncertainty calculation is usually not the best
approach. Usually Monte Carlo is both better and easier. The more
steps in the calculation, the more you gain from the Monte Carlo
approach.
7.21 OK Example: Step-by-Step Propagation
Here is an example where the propagation rules give the correct
answer. For a counterexample, see section 7.23.
Suppose somebody asks you to carry out the computation indicated on
the RHS of equation 49. If you wish, for
concreteness you may imagine that the first number is a raw
observation, the second number is some scale factor or conversion
factor, and the third number is some baseline that must be subtracted
off.
|
x = 4.4[⁄] × 2.617[⁄] − 9.064[⁄]
(49) |
As always, the [⁄] indicates that the uncertainty results from
roundoff, and is a half-count in the last decimal place. That means
we can restate the problem as 4.4±.05 × 2.617±.0005 −
9.064±.0005, with due regard for the fact that roundoff errors
are never Gaussian distributed. In this example, for simplicity, we
assume the roundoff errors follow a rectangular distribution.
Using the usual precedence rules, we do the multiplication first.
According to the propagation rules in section 7.20, we will
need to convert the absolute uncertainties to relative uncertainties.
That gives us: 4.4±1.14% × 2.617±0.02%. When we carry
out the multiplication, the result is 11.5148±1.14%. Note that
the uncertainty in the product is entirely dominated by the
uncertainty in the first factor, because the uncertainty in the other
factor is relatively small.
Next we convert back from relative to absolute uncertainties, then
carry out the subtraction. That results in 11.5148±0.131 −
9.064±.005 = 2.4508±0.131.
Now we have to decide how to present this result. One reasonable
possibility would be to round it to 2.45±0.13 or equivalently
2.45(13). One could maybe consider heavier rounding, to
2.5(1). Note that this version differs from the previous version by
39% of an error bar, which seems like a nasty thing to do to
your data.
Trying to express the foregoing result using sig digs would be a
nightmare, as discussed in more detail in
section 17.5.4. Expressing the result properly,
e.g. 2.45(13), is no trouble at all.
7.22 Amplification of Uncertainty
The calculation set forth in equation 49 is an example of
what we call a noise amplifier. We started with three numbers,
one of which had about 1% relative uncertainty, and the others much
less. We ended up with more than 5% relative uncertainty.
This is not a problem with the step-by-step approach; Monte
Carlo would have given you the same result.
It appears that the uncertainty grew during the calculation, but you
should not blame the calculation in any way. The calculation did not
cause the uncertainty; it merely made manifest the uncertainty that
was inherent in the situation from the beginning.
As a rule of thumb: Any time you compute a small difference between
large numbers, the relative uncertainty will be magnified.
If you have a noise amplifier situation that results in unacceptable
uncertainty in the final answer, you will need to make major changes
and start over. In some cases, it suffices to a more precise
measurement of the raw data. In other cases, you will need to make
major architectural changes in the experimental apparatus and
procedures, perhaps using some sort of “null” technique (electrical
bridge, acoustical beats, etc.) so that subtracting off such a large
“baseline” number is not required.
7.23 Counterexample: Step-by-Step Propagation
Let’s carry out the calculation of the pH along the lines suggested in
section 7.8. We assume a dilute solution of a weak-ish
acid:
|
CHA | | = | | 10−5 | ± 1% |
| Ka | | = | | 10−3 | ± 10% |
| (50)
|
We can find the pH by direct application of the lame “textbook”
version of the quadratic formula. If you understand what’s going on,
you know that the actual relative uncertainty in the pH is one
percent. The Crank Three Times™ method gives the
correct answer, namely one percent.
In this section we will compare the correct result with the result we
get from propagating the uncertainty step-by-step, using the rules set
forth in section 7.20.2 ... except that we will not
pay attention to the provisos and limitations that are contained in
the rules.
Here is a snapshot of the spreadsheet (reference 24) used to
carry out the calculation. The final pH has a calculated uncertainty,
highlighted with boldface, that is off by about three orders of
magnitude. The explanation is that in one of the steps, we subtracted
two numbers with highly correlated uncertainties, violating one of the
crucial provisos.
| symbol | meaning | numerical | abs uncertainty | | rel uncertainty | |
| | | | | | | |
| a | 1 | 1 | 0 | –> | 0.00% | |
| b | Ka | 0.001 | 0.0001 | <– | 10.00% | |
| | Cha | 1e-05 | 1e-07 | <– | 1.00% | |
| c | -Ka Cha | -1e-08 | 1.005e-09 | <– | 10.05% | |
| b**2 | | 1e-06 | 2e-07 | <– | 20.00% | |
| 4ac | | -4e-08 | 4.02e-09 | <– | 10.05% | |
| b**2 - 4ac | | 1.04e-06 | 2e-07 | –> | 19.23% | |
| sqrt(..) | | 0.00102 | 9.808e-05 | <– | 9.62% | |
| | | | | | | |
| -b + sqrt() | | 1.98e-05 | 0.0001401 | –> | 707.28% | |
| ../2 | pH | 9.902e-06 | 7.003e-05 | –> | 707.28% | <<< |
| | | | | | | |
| -b - sqrt() | unphysical | -0.00202 | 0.0001401 | –> | 6.93% | |
| ../2 | big root | -0.00101 | 7.003e-05 | –> | 6.93% | |
There are two parts to the lesson here:
- The step-by-step propagation rules contain lots of provisos that
must be taken seriously.
- In practice, if the provisos are being violated, it is not
necessarily easy to notice until it is too late.
In this example, the problem is so large as to be obvious. However,
beware that in other situations, you could easily make a mistake that
is not quite so conspicuous ... just wrong enough to be fatal, but
not wrong enough to be noticeable until it is too late.
Hint: If you want to see some less-obvious mistakes, try modifying
this example by increasing the concentration and/or decreasing the
uncertainty on the concentration.
Note that the more numerically-stable version of the quadratic
formula, equation 17, does slightly better, but
still does not play nicely with the step-by-step propagation rules.
It gets an uncertainty that is off by “only” about one order of
magnitude.
Also keep in mind that no matter what you are doing, you can always
make it worse by using sig figs. Section 7.8 shows how
sig figs can do insane amounts of damage to the quadratic formula in
general and pH calculations in particular.
7.24 Curve Fitting – Least Squares and Otherwise
The basic scenario goes like this: We start with some raw data. The
distribution over raw data has some uncertainty. We choose a model
that has some adjustable parameters. We run the data through the
curve-fitting process. This gives us a set of best-fit parameters.
There will be some uncertainty associated the parameters.
There are methods for estimating the uncertainty, based on what we
know about the model and the distribution of raw data. This can be
considered a form of step-by-step analytic propagation of the kind
considered in section 7.20. As such, it might work or
it might not. It is, as the saying goes, a checkable hypothesis.
After doing the calculation, it is rather easy to wiggle the
parameters and confirm that the fitted model is behaving in a way that
is consistent with the estimated uncertainties.
For the next level of detail on this, see reference 25.
7.25 Choosing a Method of Propagation
There are some simple situations where simple approaches provide
accurate propagation and/or provide useful insight. In these
situations the simple approaches should be used and fancier
methods would be a waste of effort. For example, as mentioned in
section 7.20.2, if you know that a certain distribution
has a mean of 19 and a relative uncertainty of 10%, then if you
double every element of the ensemble you get a new distribution with a
mean of 38 and the same relative uncertainty, namely 10%. This is
easy and intuitive and gets the right answer in this situation.
Consider the following multi-way contrast:
- A) If you are dealing with pointlike raw data points, you
shouldn’t be doing any propagation anyway. The raw data
points never had any error bars to begin with, as discussed
in section 4.3.
In this case, the right answer is less laborious than
step-by-step propagation, by at least a factor of 2.
- B) Now suppose we are dealing with a cooked data blob
of the form A±B.
- B1) In cases where step-by-step first-order propagation
is valid and seems convenient, go ahead and use it.
However, there are lots of situations where the hard part is
checking the validity. After you figure that out, the calculation
is probably easy ... but you have to account for all the work, not
just the calculational crank-turning work.
If you skip the validation step, you are very
likely to get the wrong answer with no warning.
- B2) There are some cases where an exact analytic solution
exists, and you might as well use it. For example, we didn’t need
to do a Monte Carlo to find the Maxwell-Boltzmann distribution,
because Mr. M. and Mr. B. have already worked it out for us.
Even when an analytic solution exists, it might be a
good idea to check it against the Monte Carlo solution.
Analytic calculations are not infallible.
-
It is altogether too easy to drop a minus sign or
a factor of two.
- If you grab the Maxwell-Boltzmann equation for the
speed when you wanted the energy (or vice versa) you
will get the wrong answer.
- If you grab the Maxwell-Boltzmann equation for 3D
and apply it in 2D (or vice versa) you will get the
wrong answer.
Errors of this kind can be exceedingly hard to catch. However, the
Monte Carlo solution provides a very powerful check.
- B3) There are plenty of cases where Monte Carlo is
just plain easier. You only need one equation, namely
the equation for analyzing an individual data point.
This contrasts with the step-by-step approach, where (at a
minimum) you need two equations: one equation for the nominal
value ⟨X⟩ and another very-different equation for the
uncertainty [X]. Just not having to derive (and check!) this
second equation may be a significant savings. The fact that you
need 1000 iterations to collect the Monte Carlo statistics is a
negligible cost, because you don’t do that work yourself; the
computer does it.
Last but not least, there are plenty of situations where Monte Carlo
is the only option.
8 How Much Accuracy Is Enough? How Much Data Is Enough?
8.1 Why is this hard?
Suppose you are taking data. How many raw data points should you
take? How accurately should you measure each point? There are
reliable schemes for figuring out how much is enough. However, the
reliable schemes are not simple, and the simple schemes are not
reliable. Any simple rule like “Oh, just measure everything to three
significant digits and don’t worry about it” is highly untrustworthy.
Some helpful suggestions will be presented shortly, but first let’s
take a moment to understand why this is a hard problem.
First you need to know how much accuracy is needed in the final
answer, and then you need to know how the raw data (and other factors)
affect the final answer.
Sometimes the uncertainties in the raw data can have less effect than
you might have guessed, because of signal-averaging or other clever
data reduction (section 7.12) or because of anticorrelated
errors (section 7.16). Conversely, sometimes the uncertainties
in the raw data can be much more harmful than you might have guessed,
because of correlated errors, or because of unfavorable leverage, as
we now discuss.
As an example of how unfavorable leverage can hurt you, suppose we
have an angle theta that is approximately 89.3 or 89.4 degrees. If
you care about knowing tan(theta) within one part in a hundred, you
need to know theta within less than one part in ten thousand.
Whenever there is a singularity or near-singularity, you risk
having unfavorable leverage. The proverbial problem of small
differences between large numbers falls into this category, if
you care about relative error (as opposed to absolute error).
8.2 How To Do It Right – Basic Recommendations
If you are recording some points:
– Use many enough digits to avoid unintended loss of
significance.
– Use few enough digits to be reasonably convenient.
– When using a calculator, leave intermediate results
in the machine.
– Keep all the raw data.
– If you think the points have come
from some underlying distribution,
first write down the points, then
separately say what you know about the distribution.
|
|
|
|
If you are describing a distribution, and you think it can be
described in terms of its center and halfwidth:
– Express the center and halfwidth separately.
Do not try to use one numeral to express two numbers.
– Explicitly state the form of the distribution,
unless it is obvious from context.
Don’t assume all distributions are Gaussian.
|
|
|
|
There are several equally good ways of expressing the mean and
halfwidth of a distribution. It usually doesn’t matter whether the
uncertainty is expressed in absolute or relative terms, so long as it
is expressed clearly. For example, here is one common way to express
the relative uncertainty of a distribution:
Meanwhile, there are multiple ways to express the absolute uncertainty
of a distribution. The following are synonymous:
| | | | | 0.048(12) | |
(52a)
|
| | | | | 0.048±0.012 | |
(52b)
|
|
Another way of expressing absolute uncertainty is:
The “interval” or “range” notation in equation 53 has
the connotation that the probability is flat and goes to zero outside
the stated interval. A flat distribution can result from roundoff, or
from other quantization phenomena such as discrete drops coming out of
a burette. You could use either of the forms in equation 52 for such a distribution, but then there would be
questions as to whether the stated error bars represented the HWHM or
the standard deviation.
Sometimes the uncertainty can be expressed indirectly, for example by
giving a rule that applies to a whole family of distributions. See
section 6.1 for an example.
There are a couple of additional special rules for raw data, as
described in section 8.4. Otherwise, all these recommendations
apply equally well to measured quantities and calculated quantities.
Remember that a distribution has width, but an individual point
sampled from that distribution does not. For details on this, see
section 5.2 and reference 2.
Therefore, if you are recording a long list of points, there is
normally no notion of uncertainty attached to the individual points,
so the the question of how to express uncertainty on a per-point basis
does not arise. If you want to describe the distributional properties
of the whole collection of points, do that separately. Note the
contrast:
|
The Wrong Way: write down 1000 points using 2000 numbers,
i.e. one mean and one standard deviation per point.
|
|
The Right Way:
Write down the points and describe the distribution using 1002
numbers, i.e. one number per point, and then one mean and one standard
deviation for the distribution as a whole.
|
Note that there is a distinction between the mean and standard
deviation of the sample, and the sample-based estimate of the mean and
standard deviation of the population. For an explanation of this, see
reference 2.
You should report the form of the distribution, as discussed in
section 8.5. Once the form of the distribution is known, if
it is a two-parameter distribution, then any of the expressions in
equation 51 or equation 52 or perhaps
equation 53 suffice to complete the description of the
distribution.
Returning to the basic recommendations given at the start of this
section: These recommendations do not dictate an “exactly right”
number of digits. You should not be surprised by this; you should
have learned by now that many things – most things – do not have
exact answers. For example, suppose I know something is ten inches
long, plus or minus 10%. If I convert that to millimeters, I get 254
mm, ± 10%. I might choose to round that off to 250 mm, ±
10%, or I might choose not to. In any case I am not required
to round it off.
Keep in mind that there are plenty of numbers for which the uncertainty
doesn’t matter, in which case you are free to write the number (with
plenty of guard digits) and leave its uncertainty unstated. For
example, an experiment might involve ten numbers, one of which makes
an obviously dominant contribution to the uncertainty, in which case
you don’t need to obsess over the others.
When comparing numbers, don’t round them before comparing, except
maybe for qualitative, at-a-glance comparisons, and maybe not even
then, as discussed in section 8.7.
When doing multi-step calculations, whenever possible leave the
numbers in the calculator between steps, so that you retain as many
digits as the calculator can handle.8 Leaving numbers in the calculator is vastly
preferable to copying them from the calculator to the notebook and
then keying them back into the calculator; if you round them off you
introduce roundoff error, and if you don’t round them off there are so
many digits that it raises the risk of miskeying something.
Leave the numbers in the calculator
between steps.
|
|
|
|
Similarly: When cut-and-pasting numbers from one program to another,
you should make sure that all the available digits get copied. And
again similarly: When a program writes numbers to a file, to be read
back in later, it should ordinarily write out all the available
digits. (In very exceptional cases where this would incur
unacceptable inefficiency, some sort of careful data compression is
needed. Simple rounding does not count as careful data compression.)
Note that the notion of “no unintended loss of
significance” is meant to be somewhat vague. Indeed the whole notion
of “significance” is often hard to quantify. You need to take into
account the details of the task at hand to know whether or not you
care about the roundoff errors introduced by keeping fewer digits.
For instance, if I’m adjusting the pH of a swimming pool, I suppose I
could use an analytical balance to measure the chemicals to one part
in 105, but I don’t, because I know that nobody cares about the
exact pH, and there are other far-larger sources of uncertainty.
When thinking about precision and roundoff, it helps to think about
the same quantity two ways:
-
From an operational point of view, counting digits is where
the roundoff rubber means the road. You have direct control of how many
digits you keep.
- From a conceptual, data-centric point of view, it is natural
to think about roundoff errors in terms of percent or ppm or the like.
Talking about 10 ppm or 100 ppm is often vastly more expressive than
talking about 5 decimal places – not least because you can nicely
express 30 ppm if you need to, whereas writing five and half digits is
remarkably ugly.
Therefore it makes sense to use a two-step process: First figure out
how much roundoff error you can afford, and then use that to give you
a lower bound on how many digits to use.
Beware that the terminology can be confusing here: N digits is not
the same as N decimal places. Let’s temporarily focus attention on
numbers in scientific notation (since the sig-digs rules are even
more confusing otherwise). A numeral like 1.234 has four
digits, but only three decimal places. Sometimes it makes sense to
think of it in four-digit terms, since it can represent 104
different numbers, from 1.000 through 9.999 inclusive. Meanwhile
it sometimes makes sense to think of it in three-decimal-place
terms, since the stepsize (stepping from one such number to the next)
is 10−3.
If you want to keep the roundoff errors below one part in 10 to the
Nth, you need N decimal places, i.e. N+1 digits of scientific
notation. For example numbers near 1.015 will be rounded up to 1.02
or rounded down to 1.01. That is, the roundoff error is half a
percent.
Also beware that roundoff errors are not normally distributed, as
discussed in section 8.3. In multi-step
calculations, roundoff errors accumulate faster than
normally-distributed errors would. Details on this problem, and
suggestions for dealing with it, can be found in section 7.12. Additional discussion of roundoff procedures can be
found in reference 8.
The cost of carrying more guard digits than are really
needed is usually very small. In contrast, the cost of carrying too
few guard digits can be disastrously large. You don’t want to do a
complicated, expensive experiment and then ruin the results due to
roundoff errors, due to recording too few digits.
|
When in doubt, keep plenty of guard digits.
|
|
|
|
8.3 Indicating Roundoff and Truncation
In the not-too-unusual situation where the uncertainty of a
distribution is dominated by roundoff error or some similar
quantization error, the situation can be expressed using a slash in
square brackets:
This can be viewed as shorthand for 0.087[½] i.e. a roundoff
error of at most half a count in the last place. Although it is
tempting to think of this as roughly equivalent to 0.0870(5), you
have to be careful, because the distribution of roundoff errors is
nowhere near Gaussian, and roundoff errors are often highly
correlated.
- If you start with an exact number such as 5.432 and round it to
one decimal place, the roundoff error is the same every time.
- If you have relatively narrow Gaussian distribution such as
5.432(3), if you round it to one decimal place, the roundoff error
will be nearly the same almost every time.
- At the other extreme, if you have a very noisy distribution such
as 5.432(99) and round it to two decimal places, the distribution of
roundoff errors is very nearly a flat distribution. Beware that the
standard deviation will markedly smaller than the halfwidth, as
discussed in connection with figure 19.
Similarly, if the uncertainty is dominated by a one-sided truncatation
error (such as rounding down), this an be expressed using a plus-sign
in square brackets:
It is tempting to think of this as roughly equivalent to 0.0875(5),
but you have to be careful, as discussed above.
If you have a situation where there is some combination of
more-or-less Gaussian noise plus roundoff error, there is no simple
way to describe the distribution.
8.4 Keep All the Original Data
When you are making observations, the rule is that you should record
all the original data, just as it comes from the apparatus. Do not
make any “mental conversions” on the fly.
-
Don’t round off readings. If you think the last-place digit is
insignificant, record it anyway. One reason is that there is too much
chance of mistakes during mental roundoff. Another reason is that
there is the chance that roundoff could throw away some useful
information. (Remember, uncertainty is not the same as significance,
as discussed in section 14.)
- Don’t convert scale factors. For example, if the instrument is
showing 12.34 millivolts, record the reading as 12.34 mV. The reason
is that if you try to make a mental conversion from mV to V, there is
too much chance of mistakes.
- Be sure to write down the units (such as mV) explicitly. This
is particularly important with auto-ranging meters. That’s because
later, during the analysis phase, it is really embarrassing to see an
entry of 12.34 and not be sure whether it is in V or mV. (If there is
a large group of readings all with the same units, you can save some
writing if you omit the units from individual readings, provided you
include a clear annotation stating the units for the group. This uses
the same principle as the distributive law of algebra.)
- Record the non-varying quantities as well as the varying
quantities. For example, if you are measuring the (I,V) characteristic
of the collector on a bipolar transistor, don’t just record collector
current versus collector voltage; you need to record things like the
base current. If it’s the same for all (I,V) readings, you only
need to record it once, but you need to record it.
- Don’t discard readings just because you “think” they won’t be
needed.9
- Never, never, never discard readings that you think are
“wrong”. If a reading seems wild, record it anyway. Record it as
is. (Mark it with a “?” or a “???” if you wish, but record the
value as is.) If you think the sample is contaminated, make a note to
that effect in the logbook, but record the reading as is.
- Never, never, never erase or obliterate readings from the log
book. If you decide a reading is wrong, add a note explaining why
it is wrong, but leave the raw data as is. The reason is that you
might change your mind about what’s right and what’s wrong.
- If you are measuring a peak that sits on a baseline, don’t just
record the peaky part of the peak; include enough of the wings so that
you will be able to confidently establish the baseline.
We are making a distinction between the raw data and the calculations
used to analyze the data. The point is that if you keep all the raw
data, if you discover a problem with the calculation, you can always
redo the calculation. Redoing the calculation may be irksome, but it
is usually much less laborious and much less costly than redoing all
the lab work.
There is a wide class of analog apparatus – including rulers,
burettes, graduated cylinders etc. – for which the following rule
applies: It is good practice to record all of the certain digits, plus
one estimated digit. For example, if the finest marks on the ruler
are millimeters, in many cases you can measure a point on the ruler
with certainty to the nearest millimeter … and then you should
try to estimate how far along the point is between marks. If
you estimate that the point is halfway between the 13 mm and 14 mm
marks, record it as 13.5 mm. This emphatically does not indicate that
you know the reading is exactly 13.5 mm. It is only an estimate. You
are keeping one guard digit beyond what is known with certainty, to
reduce the roundoff errors. You don’t want roundoff errors to make
any significant contribution to the overall uncertainty of the
measurement. [Also, if possible, include some indication of how well
you think you have estimated the last digit: perhaps 13.5(5)mm or
13.5(3)mm or even 13.5(1)mm if you have really sharp eyes.]
There is a class of instruments, notably analog voltmeters and
multimeters, where in order to make sense of the reading you need to
look at the needle and at the range-setting knob. (This is in
contrast to digital meters, where the display often tells the whole
story.) I recommend the following notation:
| Reading | | Scale | | |
| 2.88 | | /3*300mV | |
| 2.88 | | /10*1V
| |
which is to be interpreted as follows:
| Reading | | Scale | | Interpretation |
| 2.88 | | /3*300mV | | “2.88 out of three on the 300mV scale” |
| 2.88 | | /10*1V | | “2.88 out of ten on the 1V scale” |
Note that both of the aforementioned readings correspond to 0.288
volts.
There are two things going on here: First of all, converting
on-the-fly from what the scale says (2.88) to SI units (0.288) is too
error prone, so don’t do it that way; record the 2.88 as is, and do
the conversion later. Secondly, there are two ways of getting this
reading, either most of the way up on the 300mV scale (the first line
in the table above) or partway up on the 1V scale (the second line).
It is important to record which scale was used, in case the two scales
are not equally well calibrated.
Note that the notation “/3*300mV” also tells you the algebraic
operations needed to convert the raw data to SI units: in this case
divide by 3, and multiply by 300mV.
8.5 Report the Form of the Distribution
Whenever you are describing a distribution, it is important to specify
the form of the distribution, i.e. the family from which your
distribution comes. For instance if the data is Gaussian and IID, you
should say so, unless this is obvious from context. Only after the
family is known does it make sense to report the parameters (such as
position and halfwidth) that specify a particular member of the
family.
On the other side of the same coin, people have a tendency to assume
distributions are Gaussian and IID, even when there is no reasonable
basis for such an assumption. Therefore if your data is known to be
– or even suspected to be – non-Gaussian and/or non-IID, it is
doubly important to point this out explicitly. See
section 13.8 for more on this.
8.6 The Effect of Rounding
As mentioned in section 2.1, whenever you write
down a number, you have to round it to “some” number of digits. As
mentioned in section 1.1, you should keep many enough
digits so that roundoff error does not cause any unintended loss of
significance. Therefore, we need to understand the effect of
roundoff error.
- Some numbers can be represented exactly and conveniently
using decimal notation. For example, the number of items
in a dozen is 12.
- Some numbers cannot be represented exactly in decimal notation,
so any decimal representation must involve some amount
of roundoff error. For example, the reciprocal of 12
has no exact decimal representation. We can approximate
it by 0.08333[⁄].
8.6.1 Rounding Off a Gaussian
Figure 36 shows how a Gaussian distribution is
affected by roundoff. It shows an “original” distribution and two
other distributions derived from that by rounding off, as follows:
| distribution | | representation | | remark |
| 3.8675309 ± 0.1 | | solid blue line | | original |
| 3.87 ± 0.1 | | dashed yellow line | | rounded to two places |
| 3.9 ± 0.1 | | dotted red line | | rounded to one place |
Obviously, the blue curve is the best. It is the most faithful
representation of the real, original distribution.
As I see it, the dashed yellow curve is not better, but it’s not much
worse than the original. Its Kullback-Leibler information divergence
(relative to the original) is about 0.0003. You can see that even
if you keep more digits than are called for by the sig-figs rules,
the roundoff error is not entirely negligible.
The dotted red curve is clearly worse. You can see at a glance that
it represents a different distribution. It’s K-L information divergence
(relative to the original) is more than 0.05. You can see
that following the sig-figs rules definitely degrades the data.
8.6.2 Rounding Off a Histogram
To show the effect of rounding, let’s do the following experiment,
which can done using nothing more than a spreadsheet program: We draw
a sample consisting of N=100 numbers, drawn from a source distribution,
namely a Gaussian centered at 1.17 with a standard deviation of 0.05.
As usual, the first thing to do is look at a scatter plot of the data,
as shown in figure 37. We calculate a mean of 1.164
and a standard deviation of 0.0510, so the sample is not too
dissimilar from the source distribution.
Next we round each data point to the nearest 0.01, and histogram the
results. This is shown in figure 38.
Next we round off this data to the nearest 0.1 units and histogram the
results. This is shown in figure 39. The mean and
standard deviation of the rounded data are 1.157 and 0.0624 ... which
means that the roundoff has increased the spread of the data by more
than 20%.
Rather than plotting the probability density, which is what these
histogram are doing, it is often smarter to plot the cumulative
distribution. This is generally a good practice when comparing two
distributions, for reasons discussed in reference 2. This is shown in figure 40.
The green curve is the theoretical distribution, namely the integral
of a Gaussian, which we recognize as a scaled and shifted error
function, erf(...), as discussed in reference 2.
You can see that the raw data (shown in black) does a fairly good job
of sticking to the theoretical distribution. The data that has been
rounded to the nearest 0.01 (shown in blue) does a slightly worse job
of sticking to the theoretical curve, and the data that has been
rounded to the nearest 0.1 (shown in red) does a much, much worse job.
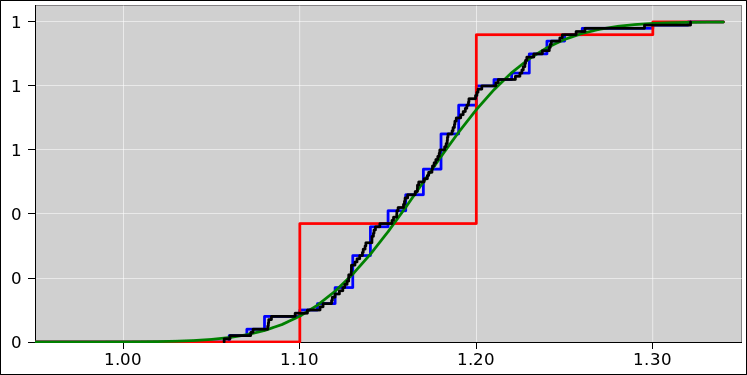 Figure 40
Figure 40: Cumulative Distribution, With and Without Rounding (100 data points)
Now let’s see what this looks like if we use a larger sample, namely
N=1000 points, as shown in figure 41. You can
see that the raw data (shown in black) is smoother, and sticks to the
theoretical curve more closely.
In the limit, by using ever-larger samples, we can make the black
curve converge to the green curve as closely as desired. The
convergence works like this: Each of the N raw data points in
figure 37 can be considered a delta function with
measure 1/N. When we integrate to get the cumulative distribution,
as in figure 40 or
figure 41, each data point results in a step,
such that the black curve rises by an amount 1/N. If you look
closely, you can see 100 such steps in figure 40.
For arbitrarily large N, the steps become arbitrarily small.
In contrast, the rounded data will always be a series of stair-steps,
due to the rounding, and the steps do not get smaller as we increase
N. In this example, the red curve will never be much better than a
two-step approximation to the error function, and the blue curve will
never be much better than a 20-step approximation. The only way to
get the rounded data to converge would be to use less and less
rounding, i.e. more and more digits.
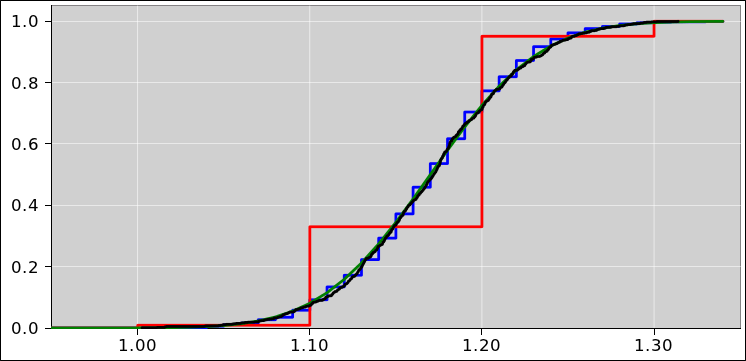 Figure 41
Figure 41: Cumulative Distribution, With and Without Rounding (1000 data points)
8.6.3 Nonuniform Relative Error
If we think in terms of relative error, aka percentage error, we see
that roundoff does not affect all numbers the same way.
Figure 42 shows the percentage error
introduced by rounding X to one significant digit, plotted as a
function of X. The function is periodic; each decade looks the
same.
For numbers near 150, the roundoff error is 33%. For numbers
near 950, the roundoff error is barely more than 5%.
The situation does not improve when the number of digits gets larger,
as you can see from figure 43.
For numbers near 105, the roundoff error is 5%. Meanwhile, for
numbers near 905, the roundoff error is an order of magnitude less.
When some quantity has been observed repeatedly
and the ensemble of observations has an uncertainty of 1%,
there is an all-too-common tendency for people to say the measurement
is “good to two significant figures”. This is a very sloppy figure
of speech, and should be avoided.
As always, the rule should be: Say what you mean, and mean what you
say.
- If you mean that a measurement is good to 1%, say it is good
to 1%. (This is not the same as two sig figs, or any other number
of sig figs.)
- If you mean a certain voltage measurement has been rounded
off to the nearest 0.01 volts, say it has been rounded off
to the nearest 0.01 volts. (This should not be expressed
in terms of significant figures, because when the voltage
is small, rounding to the nearest .01 volts will have fewer
significant digits than when the voltage is larger.)
As a rule, whenever you are tempted to say anything in terms of
significant digits, you should resist the temptation. There is almost
certainly a better way of saying it.
8.6.4 Roundoff Error is Not Necessarily Random
Note the following contrast:
|
Sometimes roundoff error looks somewhat random. If we start
with a bunch of random numbers and round them off, the roundoff errors
will exhibit some degree of randomness.
|
|
Sometimes roundoff error is
completely non-random. If we start with 1.23 and round it off to one
decimal place, we get 1.2 every time.
|
|
In some cases, the roundoff errors will be uniformly
distributed.
|
|
In some cases, even if the roundoff errors are somewhat
random, the distribution will be highly non-uniform.
|
As a slight digression, let us look at some random data
(figure 44). We shall see that it does not
look anything like roundoff errors
(figure 42 or
figure 43).
Suppose we conduct an experiment that can be modeled by the following
process: For a given value of λ, we construct a Poisson random
process with expectation value λ. We then draw a random
number from this process. We calculate the residual by subtracting
off the expected value. We then express the residual in relative
terms, i.e. as a percentage of the expected value. All in all, the
normalized residual is:
For selected values of λ we collect ten of these normalized
residuals, and plot them as a function of λ, as shown in
figure 44. The magenta curves in the
figure represent ±σ, where σ is the standard deviation
of the normalized residuals.
Our purpose here is to compare and contrast two ideas:
In both cases, the ordinate in the figure is the percentage
“discrepancy”. The style of representation is the same, to
facilitate comparing the two ideas.
Now, when we make the comparison, we find some glaring
dissimilarities.
- Figure 42 shows a function. That is,
there is a unique ordinate for every abscissa. That is because every
time we round off a given number, it rounds off the same way.
Roundoff errors are not uniformly random.
Sometimes they’re not random at all.
|
|
|
|
In contrast, the random data plotted in
figure 44 is not a function. There are
ten different residuals (the ordinate) for each value of λ
(the abscissa).
- The roundoff error incurred when rounding off X is a periodic
function of log10(X). In contrast, the relative uncertainty in
a Poisson process is a smooth monotone decreasing function of
λ.
8.6.5 Correlations
Here is a good estimate for the mass of the earth, as discussed in
section 9.3:
Looking at this value, you might be tempted to think that the nominal
value has several insignificant digits, five digits more than seem
necessary, and six or seven digits more than are allowed by the usual
idiotic sig figs rules. It turns out that we will need all those
“extra” digits in some later steps, including forming products such
as GM⊕ and ratios such as M⊕/M⊙, as discussed in
section 9.
Part of the fundamental problem is that the uncertainty indicated in
equation 57 only tells us about the variance, and doesn’t
tell us about the covariance between M⊕ and other things
we are interested in.
Indeed, the whole idea of associating a single uncertainty with each
variable is Dead on Arrival, because when there are N variables, we
need on the order of N2 covariances to describe what is going on.
|
Using decent terminology, as in equation 57, we are
allowed to write down enough digits. We are allowed to keep the
roundoff error small enough, even to the point where it is several
orders of magnitude smaller than the standard deviation.
|
|
The usual
stupid sig figs rules would require us to round things off until the
roundoff error was comparable to the standard deviation. If we went
on to calculate GM⊕ or M⊕/M⊙, the result would be an
epic fail. The result would be several orders of magnitude less
accurate than it should be.
|
Indeed, decent terminology allows us take a multi-step approach, which
is usually preferable: First, write down M⊕ = 5.9725801308
×1024 kg, with no indication of uncertainty.
Similarly, write down all the other quantities of interest, with no
indication of uncertainty. In a later step, write down the full
covariance matrix, all in one place.
It is permissible to write something like M⊕ = (5.9725801308
± 0.00071)×1024 kg, but indicating the uncertainty
in this way is possibly misleading, and at best redundant, because you
are going to need to write down the covariance matrix eventually. The
variances are the diagonal elements of the covariance matrix, and this
is usually the best way to present them.
In the exceptional case where all the variables are uncorrelated, the
covariance matrix is diagonal, and we can get away with using simple
notions of “the” uncertainty “associated” with a particular
variable.
See section 9.
8.7 Comparisons, with or without Rounding
One of the rare situations where rounding off might arguably be
helpful concerns eyeball comparison of numbers. In particular,
suppose we have the numbers
|
a | | | | b |
| 1.46 | | | | 1.45883 |
| 1.46 | | | | 1.48883
|
| (58)
|
and we are sure that a half-percent variation in these numbers will
never be significant. From that we conclude that on the first line
there is no significant difference between a and b, while on
the second line there is. Superficially, it seems “easier” to
compare rounded-off numbers, since rounding makes the similarities and
differences more immediately apparent to the eye:
However, rounding is definitely not the best way to facilitate
comparisons. Rounding can get you into trouble. For example, if
3.4997 gets rounded down to 3 and 3.5002 gets rounded up to 4, you can
easily get a severely false mismatch. On the other side of the same
coin, if 3.5000 gets rounded up to 4, and 4.4997 gets rounded down to
4, you get a false match. Once again, we find that aggressive
rounding produces wrong answers. Note that the sig-figs rules
require aggressive rounding.
It is far more sensible to subtract the numbers at full precision,
tabulate the results (as in equation 60), and then
see whether the magnitude of the difference is smaller than some
appropriate amount of “fuzz”.
|
a | | | | b | | b−a | | flag |
| 1.46 | | | | 1.45883 | | −0.00117 | | |
| 1.46 | | | | 1.48883 | | +0.02983 | | <<< |
| (60)
|
If you are doing things by computer, computing the deltas is no harder
than computing the rounded-off versions, and you should always write
programs to display the deltas without rounding. (Here “delta” is
shorthand for the difference b−a.) While you are at it, you might
as well have the computer display a flag whenever the delta exceeds
some configurable threshold.
Compared to equation 58 or even
equation 59, the advantage goes to
equation 60. It makes it incomparably less likely
that important details will be overlooked.
Even if you are doing things by hand, you should consider calculating
the deltas, especially if the numbers are going to be looked at more
times than they are calculated. It is both easier and less
error-prone to look for large-percentage variations in the deltas than
to look for small-percentage variations in the original values.
8.8 Guard Digits
Guard digits are needed to ensure that roundoff error does not become
a significant contribution to the overall uncertainty. An
introductory example is discussed in section 7.3.
The need for guard digits is also connected to the fact that
uncertainty is not the same as insignificance. The distinction
between significance, overall uncertainty, and roundoff error is well
illustrated by examples where there are uncertain digits whose
significance can be revealed by signal averaging, such as in section 7.12, section 17.4.4,
section 12, and especially figure 51 in
section 14.
Another phenomenon that drives up the need for guard digits involves
correlated uncertainties. A familiar sub-category comprises
situations where there is a small difference between large
numbers. As an example in this category, suppose we have a meter
stick lying on the ground somewhere at NIST, in Gaithersburg, oriented
north/south. We wish to record this in a Geospatial Information
System (GIS). Let point A and point B represent the two ends of
stick. We record these in the database in the form of latitude and
longitude (in degrees), as follows:
|
A | | = | | ( 39.133 430 0000 ± 0.002 N, | 77.221 484 000 ± 0.002 W) |
| B | | = | | ( 39.133 439 0075 ± 0.002 N, | 77.221 484 000 ± 0.002 W)
|
| (61)
|
The uncertainty of ± 0.002 represents the fact that the location
of the stick is known only approximately, with an uncertainty of a
couple hundred meters.
You may be wondering why we represent these numbers using nine decimal
places, when the sig-figs doctrine says we should use only three. The
answer is that the difference between these two vectors is known
quite accurately. The difference |A−B| is 0.000 009 0075(90) degrees of
latitude, i.e. one meter, with an uncertainty of ± 1 millimeter or
less.
We emphasize that the absolute uncertainty in A−B is on the order of
a millimeter or less, whereas the uncertainty in A or B separately
is several orders of magnitude greater, on the order of hundreds
of meters.
Remember: As mentioned in section 2.1,
section 6.3, section 8.8, and
section 17.1, roundoff error is only one
contribution to the overall uncertainty. The uncertainty in A or
B separately is on the order of 0.002, but that does not tell you
how much precision is needed. The sig figs approach gets the
precision wrong by a factor of a million. Situations like this come
up all the time the real world, including GIS applications and
innumerable other applications.
8.9 «Final» Results : Guard Digits; Actual Significance
There are two situations that must be considered. In one case your
best efforts are required, and in the other case maybe not.
- We start by considering the case where your best efforts are
required. For example, suppose you are a metrologist, and your job is
to measure this-or-that fundamental constant to high precision. You
wouldn’t be bothering to do that if the published “handbook” value
was good enough. You are part of a team, and the downstream members
of the team need all the precision you can give them.
Here’s another scenario that leads to the same conclusion: Sometimes
you measure something before you know what it’s going to be used
for. Many fundamental constants are in this category. Again, common
sense says you should report your best results; you should not degrade
your results by rounding. In other words, your final results should
have plenty of guard digits.
Suppose you have a calculation with a great many intermediate steps.
This this is quite common, especially when using an iterative
algorithm. In this case you may need an extra-large number of guard
digits on the intermediate results, to prevent an accumulation of
roundoff error. You still need some guard digits on the bottom-line
result, but perhaps not quite so many.
|
Hypothetically, sometimes people imagine they can quote their
«final» result using sig figs (even though they used plenty of guard
digits on the intermediate results).
|
|
In reality, you have to assume
somebody is going to use your result. Therefore your “final
output” is somebody else’s input. An example of this can be seen in
the teamwork scenario in section 7.10.3. In any
case, from an overall point of view, all results are intermediate
results, and all of them need guard digits.
|
|
|
|
Applying sig figs to the supposedly «final» result is a
blunder. It does horrendous damage to the «final» result (both the
nominal value and the uncertainty). Don’t do it.
|
|
Hypothetically, if you tried to make guard digits compatible
with sig figs, you would need to invent some new notation so that at
each step of the calculation you could distinguish the so-called
significant digits from the guard digits.
|
|
In reality, I’ve never seen
anybody try to distinguish guard digits from other digits. It’s too
much work for too little benefit. Anybody who cares enough to go to
that much trouble presumably knows about easier and better methods.
|
|
|
|
In reality, you do not need to keep track of exactly how
many guard digits there are, so long as there are enough.
|
|
Hypothetically, sometimes people imagine the following excuse
for rounding off the «final» answer: Suppose there is an academic
busywork assignment, where nobody really cares about the answer. The
teacher unwisely decides that it is OK for everybody to get an
unrealistic answer, so long as everybody gets the same answer.
In this situation, conformity is more important than integrity.
|
|
In
reality, this is a terrible lesson. Don’t do it. Instead, accept the
fact that real-world numbers have guard digits, and the guard digits
will be noisy. Accept the fact that not all correct answers will be
numerically identical. Make academic exercises as authentic as
possible. Insist on integrity in all that you do.
|
- Here’s a slightly artificial scenario: Suppose you work in the
Quality Assurance department in a large manufacturing plant. A batch
of widgets has arrived from your supplier. You test them to see
whether they conform to specifications. The contract gives you only
two options: Accept or reject the batch. Pass or fail. Green light
or red light. In other words, after all your measurements, the final
result necessarily gets rounded to a single bit ... not even one
decimal digit, just one bit. Any additional resolution would be
insignificant in the strict sense, i.e. it would be immaterial.
In this scenario, the appropriate roundoff is determined by what
happens downstream of your decision. This stands in stark contrast
to the “propagation of error” techniques that are used in
conjunction with sig figs, where the amount of rounding is determined
by what happens upstream of your result. The fig-figs minions refer
to this as «significance» but that’s an abuse of the word; when you
calculate the uncertainty using propagation-of-error (or Crank Three
Times™ or any other method), that does not tell you
whether or not the uncertainty is significant in the strict
sense. Real significance depends details of what happens downstream.
This QA scenario is slightly artificial, for the following reason: If
the supplier had any sense, they would negotiate a better contract.
They would ask you to report your testing results in detail, in
addition to the pass/fail grade. This is particularly important in
the case of a fail or a marginal pass, to help the supplier tighten
up their process.
You can argue both sides of this forever:
- Sometimes there are categorical, discrete decisions: pass or
fail, ball or strike, rocket-launch go or no-go, et cetera.
- Even so, in the case of a close call, it is worth recording in
detail the factors that went into the decision, for later analysis.
Furthermore, even in situations that appear discrete, it is sometimes
necessary to have tie breakers. For example, things like graduation
or promotion to a higher rank are to a first approximation yes/no
decisions. However, if there are two military officers with the same
rank, the one who has held that rank longer is senior to the other
... and in rare occasions this actually matters.
Bottom line: In most cases, you should record your final answer
with plenty of guard digits, to protect it from roundoff error.
If there is the slightest doubt, keep plenty of guard digits.
In other words: sometimes quantizing the «final» result is
the right thing to do ... but sometimes it isn’t. Do not make
a habit of throwing away the guard digits.
It should go without saying that sig figs is never the right reason or
the right method for rounding your results. If/when you need to state
the uncertainty, state it separately and explicitly, perhaps using the
notation 1.234(55) or 1.234±0.055 or the like.
8.10 Too Many Digits, Oh My!
I often get questions from people who are afraid there will
be an outbreak of too many insignificant digits. A typical
question is:
“What if a student divides 10 meters by 35 seconds
and reports the result as 0.285714286 m/s? Isn’t that just wrong?
In the absence of other information, it implies an uncertainty of
0.0000000005 m/s, which is a gross underestimate, isn’t it?”
My reply is always the same: No, those «extra» digits are not wrong,
and they do not imply anything about the uncertainty.
Yes, I see nine digits, but no, that doesn’t tell me the uncertainty.
The uncertainty might be much greater than one part in 109, or it
might be much less. If the situation called for stating the
uncertainty, I might fault the student for not doing so. However, there
are plenty of cases where the uncertainty does not need to be
expressed, and may not even be knowable, in which case the only smart
thing to do is to write down plenty of guard digits.
Suppose we later discover that the overall relative uncertainty was
10%. Then I interpret 0.285714286 as having eight guard digits. Is
that a problem? I wish all my problems were as trivial as that.
If you think excess digits are a crime, we should make the punishment
fit the crime. Let’s do the math:
-
Black&white printing costs about a penny a page;
- There are about 500 words to a page;
- Each over-long numeral such as 0.285714286 means there will be
an entire word less that fits on the page.
- Therefore each student who perpetrates such a crime will be
fined 20 microbucks for each offense.
- I figure if a student does that twice a day, every day, all term, at
the end of the term he will have to give me one gummi-bear, to pay off
the accumulated fines.
My time is valuable. The amount of my time wasted by people who are
worried about the «threat» of excess digits greatly exceeds the
amount of my time wasted reading excess digits.
My advice: Breathe in. Breathe out. Relax already. Excess digits
aren’t going to hurt you. They might even help you.
The cost of keeping a few guard digits
is often very very small.
The value of keeping a few guard
digits is often very very great.
|
|
|
|
8.11 How To Avoid Introducing Sig Figs
In an introductory course, the most sensible approach is to
adopt the following rules:
-
Record the observed raw data to full precision.
- Unless/until you are told otherwise, in this course it suffices to:
-
- – do all intermediate calculations to 6-digit precision or better
- – round the final answer to 3 digits, as the very last step.
This is much simpler than dealing with sig figs. It also more honest.
Reporting no information about the uncertainty is preferable to
reporting wrong information about the uncertainty (which is what you
get with sig figs).
If the students are “mathematically challenged” and even “reading
challenged”, it is a safe bet that they are not doing multi-digit
calculations longhand. And they probably aren’t using slide rules
either. So let’s assume they are using calculators. Therefore the
burden of keeping intermediate results to 6-digit precision or better
(indeed much better) is negligible. It has the advantage of getting
them in the habit of keeping plenty of guard digits.
Yes, some of those digits will be insignificant. So what?
Extra digits will not actually kill anybody.
At some point in the course, we want the students to develop “some”
feeling for uncertainty. So let’s do that. We can do it easily and
correctly, using the Crank Three Times™ method as
described in section 7.14. (Apply it to selected problems now
and then, not every problem.) It requires less sophistication,
requires less effort, and produces better results –
compared to anything involving sig figs.
Using sig figs is like trying to eat a bowlful of clear soup using a
fork. It’s silly, especially since spoons are readily available.
Even if somebody has a phobia about spoons, the fork is still silly;
they’d be better off throwing it away and using no utensil at all.
8.12 Psychological Issues
In an introductory course, some students (especially the more
thoughtful students) will be appalled by the crudity and unreliability
of the sig figs doctrine, and will appreciate the value of guard
digits.
On the other hand, there will also be some students (especially the
more insecure students) for whom various psychological issues make it
hard to appreciate the necessity for guard digits. These issues
include the following:
- First, there is something I call barnyard ethology. One of the
rules of the barnyard is to never admit weakness. For example, an
injured sheep will go to amazing lengths to conceal its injury. This
makes sense, because if a sheep is seen to be injured, not only will
the wolves pick on it, the other sheep will pick on it. (This leads to
the old farmer’s saying that “a sick sheep is a dead sheep”. That
saying arises because by the time it becomes obvious that a sheep is
ill, it is very gravely ill.)
This rule of barnyard ethology applies to some spheres of human
activity, including lawyering, politics, and military combat.
Never admit weakness, and never admit uncertainty.
However ... students need to realize that science is not like
lawyering, or politics, or combat. Scientists do admit
uncertainty. The surest way to be recognized as a non-scientist is to
pretend to be certain when you’re not.
It may seem ironic or even paradoxical, but it is true: One of the
most basic steps toward reducing uncertainty is to admit that there is
some uncertainty, and to account for it. For example, it would always
be wrong to say that the true voltage is 1.23 volts, whereas we might
be quite confident that the true voltage is in the range bewteen 1.22
and 1.24 volts. For more on this, see
reference 26.
Being able to admit uncertainty requires some emotional maturity, some
emotional security, some grownupness. This is an important part of
why students go to school, to learn such things.
- As mentioned in section 5.6, some students think
that being wrong is Wrong with a capital W, in the same way that
lying and stealing are Wrong, i.e. sinful. They tell themselves,
perhaps unconsciously, that if they write down a number with guard
digits, there will be uncertainty in the guard digits, which is to say
those digits might be wrong, i.e. Wrong, i.e. sinful. Therefore they
refuse to write into their logbooks anything that has the slightest
uncertainty. They adore the sig figs doctrine, especially the
half-count sect, because it allows them to keep rounding until all the
uncertain digits have been eliminated.
This is spectacularly unscientific. By rounding off the number to the
point where it is not fluctuating, they have arranged to get the same
number every time ... but it is wrong every time. It is wrong
because of excessive roundoff error. Evidently they would rather be
wrong with certainty than right with uncertainty.
- Some students have been trained to not say anything or write
anything unless they are sure that it is “true”.
They need to realize that when they write down raw observations, with
or without guard digits, they are recording the indicated values, not
the true values. The indicated value represents the range of
true values, but it is not the same thing.
When describing a distribution, don’t worry about the fact that the
description is non-unique. There are lots of ways of describing the
same distribution. If it makes you feel better, first write
down the width of the distribution, and then write down the
nominal value. If the distribution has a half-width of ±7%, it
doesn’t matter whether you express the nominal value as 51, or 51.13,
or 51.1394744. The fact that the trailing digits are uncertain and
non-unique doesn’t make these numbers wrong. They are all equivalent,
for almost all practical purposes.
If you were to claim that any number such as 51, or 51.13, or
51.1394744 (with or without guard digits) represented an exact
measurement, that would be wrong. So don’t pretend it’s exact. Say
it has an uncertainty of ±7%. Once you’ve said that, you are
free to write down as many guard digits as you like. (You need at
least some uncertain digits, to guard against roundoff errors.)
- Students want certainty. Indeed, everybody wants certainty.
Alas, you can’t always get what you want.
The real world does not offer certainty. Students should not blame
themselves for uncertainty, and should not blame the teacher. We live
in an uncertain world. The goal is not to eliminate all uncertainty;
the goal is to learn how to live in an uncertain world.
One of the crucial techniques for dealing with uncertainty is to
represent things as distributions rather than as plain numbers.
- We turn now from the normal range of uncertainty to outright mistakes.
The goal is not to avoid all mistakes. Everybody makes mistakes.
Students are expected to make more mistakes than professionals, but
even professionals make mistakes. The goal is to (a) minimize the
cost of the mistakes, and (b) learn from the mistakes. For example,
real-world engineers commonly build pilot plants and/or carry out
pilot programs, so they can learn from mistakes relatively cheaply,
before they commit to a multi-billion-dollar full-scale program.
For more along this line, see section 8.14.
I have seen students go to great lengths to avoid having the
slightest imperfection in their lab books. These students need to
realize that real science involves approximation, including what we
call successive refinement. That is, we first make a rough
measurement, and then based on what we just learned, we make
successively more refined measurements. If the first measurement were
perfect, we wouldn’t need the later measurements. Learning is not a
sin.
8.13 How To Survive an Attack of Sig Figs
There are two issues: writing sig figs, and reading sig figs.
If you ever feel you need to write something using sig figs, you
should lie down until the feeling goes away. Figure out what you are
trying to say, and find a better way of saying it. If you are going
to express the uncertainty at all, express it separately. See also section 8.11.
The rest of this section is devoted to reading sig figs. That is,
suppose you are given a bunch of numbers and are required to
interpret them as having significant digits.
If that’s all you have to go on, it is not necessary – and not
possible – to take the situation seriously. If the authors had
intended their uncertainties to be taken seriously, they would
have encoded the data properly, not using significant digits.
Sometimes, though, you do have more information available.
One good strategy, if possible, is to simply ask the authors what they
think the data means. If the data is from a book, there may be a
statement somewhere in the book that says what rules the authors are
playing by. Along similar lines, I have seen blueprints where
explicit tolerance rules were stated in the legend of the blueprint:
one example said that numbers with 1, 2, or 3 decimal places had a
tolerance of ±0.001 inches, while numbers with 4 decimal places
had a tolerance of ±0.0001 inches. That made sense.
Another possibility is to use your judgment as to how much
uncertainty attaches to the given data. This judgment may be based
on what you know about the source of the data. For instance, if you
know that the data results from a counting process, you might decide
that 1100 is an exact integer, even though the sig figs rules might
tell you it had an uncertainty of ±50 or even ±500 or worse.
As a next-to-last resort, you can try the following procedure. We
need to attribute some uncertainty to each of the given numbers.
Since we don’t know which sect of the sig-digs cult to follow, we
temporarily and hypothetically make the worst-case assumption,
namely just shy of ten counts of uncertainty in the last place. For
example, 1.23 becomes 1.23±0.099, on the theory that 1.23±0.10
would have been rounded to 1.2 according to the multi-count sect.
(The multi-count sect is generally the worst case when you are
decoding numbers that are already represented in sig-figs
notation. Conversely, the half-count sect is generally the worst case
when you are encoding numbers into the sig-figs representation,
because it involves the greatest amount of destructive rounding.)
Now turn the crank. Do the calculation, using plenty of guard digits
on the intermediate results. Propagate the uncertainty using the
methods suggested in section 7.
Now there are two possibilities:
I categorically decline to suggest an explicit convention as to what
sig figs “should” mean. There are two reasons for this: First of
all, the sectarian differences are too huge; anything I could say
would be wildly wrong, one way or the other, according to one sect or
another. Secondly, as previously mentioned, what’s safest when
writing sig figs is not what’s safest when reading and trying to
interpret sig figs. Last but not least, sig figs “should” not be
used at all; I don’t want to say anything that could be misinterpreted
as endorsing their use.
8.14 Sensitivity Analysis, On-Line Analysis, and Cross-Checking
Spreadsheets are great. You need to analyze the data one way or
another, so you might as well do it on a spreadsheet. This gives you
a big bonus: you can do some “what-if” analysis. You don’t need to
do a full-blown Monte Carlo analysis as in section 7.16; instead
just wiggle a few of your data points to see how that affects the
final answer. The same goes for other quantities such as calibration
factors: find out how much of a perturbation is needed to
significantly affect the final answer.
If good-sized changes in a data point have negligible effect on the
final answer, it means you can relax a bit; you don’t need to drive
yourself crazy measuring that data point to extreme precision.
Conversely, if you find that smallish changes in a single data point
have a major effect on the answer, it tells you that you’d better
measure each such data point as accurately as you can, and/or you’d
better take a huge amount of data (so you you can do some
signal-averaging, as discussed in section 7.12). You can
also consider upgrading the apparatus, perhaps using more accurate
instruments, and/or redesigning the whole experiment to give you
better leverage.
There is a lesson here about procedures: It is a really bad idea to
take all your data and then do all your analysis. Take some
data and do some analysis, so you can see whether you’re on the
right track and so you can do the sensitivity analysis we just
discussed. Then take some more data and do some more analysis. This
is called on-line analysis.
This is quite important. As mentioned in section 8.12, real-world
engineers commonly build pilot plants and/or carry out pilot programs,
so they can learn what the real issues are before they commit to
full-scale production. Once the program is in operation, they do a
lot of trend monitoring, so that if a problem starts to develop about
it they learn about it sooner rather than later.
You should also find ways to make internal consistency checks. If
there are good theoretical reasons why the data should follow a
certain functional form, see if it does. Exploit any sum rules or
other constraints you can find. Make sure there is enough data to
overconstrain the intended interpretation. By that I mean do not rely
on two points to determine a straight line; use at least three and
preferably a lot more than that, so that there will be some internal
error checks. Similarly, if you are measuring something that is
supposed to be a square, measure all four sides and both diagonals if
you can. Measure the angles also if you can.
There are few hard-and-fast rules in this business. It involves
tradeoffs. It involves judgment. You have to ask: What is the cost
of taking more data points? What is the cost of making them more
accurate? What is the cost of a given amount of uncertainty in the
final answer?
Additional good advice can be found in reference 27.
9 Correlation and Covariance
9.1 Example: Electron Charge-to-Mass Ratio
If you want to calculate the electron e/m ratio, correlations must
be taken into account. This is discussed in section 7.7.
9.2 Example: Common Mode versus Differential Mode
Consider the simplified ohmmeter circuit shown in
figure 45
 Figure 45
Figure 45: Common-Mode and Differential-Mode Signals
In such a circuit, it would not be uncommon to find the following
voltages:
|
VA | | = | | 0.51 | ± | 1 V | relative to chassis ground |
| VB | | = | | 0.5 | ± | 1 V | relative to chassis ground |
| (62)
|
The question arises, what is the differential-mode signal VA − VB?
If you thought VA and VB were uncorrelated, you would calculate
|
ΔV | | = | | VA − VB | |
| | | = | | 0.01 ± 1.4 V | | ☠
|
| (63)
|
However, in the real world, with a little bit of work you could
probably arrange for VA and VB to be very highly correlated.
It might turn out that
|
ΔV | | = | | 0.01 | ± | 0.0001 V | | (possibly)
|
| (64)
|
and with extra work you could do even better. There is no way to
calculate the result in equation 64, not without a
great deal of additional information, but that’s not the point. The
point is that assuming the voltages are uncorrelated would be a very
very bad assumption. The physics of the situation is that the stray
time-dependent magnetic flux φ· affects both VA and VB in the same way, to an excellent approximation. Communications
equipment and measuring instruments depend on this. It’s not
something that happens automatically; you make it happen by
careful engineering.
9.3 Example: Mass and Gravitation (I)
Let’s do an example involving Newton’s constant of universal
gravitation (G), the mass of the earth (M⊕), and the product
of the two (GM⊕).
In order to speak clearly, we introduce the notation D(M⊕) to
represent a direct measurement of M⊕. We use the unadorned
symbol M⊕ to represent our best estimate of M⊕. If
necessary, we can use T(M⊕) to represent the true, ideal,
exact value, which will never be known by mortal man.
The last time I checked,
|
| | quantity | | direct measurement | | best estimate | | relative uncertainty |
| G | | D(G) | | G = D(G) | | 100 parts per million |
| GM⊕ | | D(GM⊕) | | GM⊕ = D(GM⊕) | | 2 parts per billion |
| M⊕ | | not available | | M⊕ = D(GM⊕)/D(G) | | 100 parts per million |
|
(65) |
You could obtain an estimate of M⊕ from geology and seismology, but
even that wouldn’t count as a “direct” measurement, and more
importantly it wouldn’t be particularly helpful, since it would not be
anywhere near as accurate as D(GM⊕)/D(G).
Here are the actual nominal values and absolute uncertainties, from
reference 28 and reference 29:
|
G | | = | | | ×10−11 m3kg−1s−2 |
| GM⊕ | | = | | ⎛
⎜
⎝ | | | 3.9860044180 |
| ± | 0.0000000080
|
| ⎞
⎟
⎠ |
| ×1014 kg3s−2 |
| M⊕ | | = | | | ×1024 kg |
| (66)
|
Looking at the value for M⊕ in equation 66, you
might be tempted to think that the nominal value has several
insignificant digits, five digits more than seem necessary, and six or
seven digits more than are allowed by sig figs doctrine. However, it
would be a Bad Idea to round off this number. Note the contrast:
|
Suppose you keep all the digits in
equation 66. If you multiply M⊕ by G, you get
a good value for the product GM⊕, accurate to 2 ppb.
|
|
Suppose
you round off the nominal value for M⊕. If you then multiply
by G, you get a much less accurate value for GM⊕, accurate to
no better than 100 ppm.
|
The fundamental issue here is the fact that M⊕ is highly
correlated with G. They are correlated in such a way that
when you multiply them, the uncertainty of the product is vastly less
than the uncertainty in either one separately.
|
Yes, the distributions governing G and M⊕ have
considerable uncertainty.
|
|
No, you should not round off those
quantities to the point where roundoff error becomes comparable to the
uncertainty; that would be ludicrously destructive.
|
To better understand this situation, it may help to look at the
diagram shown in figure 46. Recall from
section 5.2 that fundamentally, an “uncertain quantity”
such as G or M⊕ is really a probability distribution. Also
recall that as a general principle, you can always visualize a
probability distribution in terms of a scatter plot. In this case, it
pays to plot both variables jointly, as a two-dimensional scatter
plot. In figure 46, G is plotted horizontally and
its standard deviation is shown by the magenta bar. Similarly
M⊕ is plotted vertically its standard deviation is shown by the
blue bar. The standard deviation of the product GM⊕ is
represented – loosely – by the yellow bar.
In this figure, the amount of correlation has been greatly
de-emphasized for clarity. The uncertainty of the product is
portrayed as only six times less than the uncertainty of the raw
variables. (This is in contrast to the real physics of mass and
gravitation, where the uncertainty of the product is millions of times
less than the uncertainty of the raw variables.)
If the probability distribution is a two-dimensional Gaussian, the
contours of constant probability are ellipses when we plot the
probability as in figure 46. If the variables are
highly correlated, the ellipses are highly elongated, and the
principal axes of the ellipse are nowhere near aligned with the axes
of the plot. (Conversely, in the special case of uncorrelated
variables, the axes of the ellipse are aligned with the axes of the
plot, and the ellipse may or may not be highly elongated.)
This example serves to reinforce the rule that you should not round
off unless you are sure it’s safe. It’s not always easy to figure out
what’s safe and what’s not. When in doubt, keep plenty of guard
digits.
9.4 Dealing with Correlations
To make progress, we need to construct the covariance matrix. It is
defined as:
|
Σ(x1, x2) | | := | | ⎡
⎢
⎣ | | ⟨[x1−x̅1][x1−x̅1]⟩ | | ⟨[x1−x̅1][x2−x̅2]⟩ |
| ⟨[x2−x̅2][x1−x̅1]⟩ | | ⟨[x2−x̅2][x2−x̅2]⟩ |
| ⎤
⎥
⎦ |
|
| | |
| | | = | | | ⟨ | ⎡
⎢
⎣ | | [x1−x̅1][x1−x̅1] | | [x1−x̅1][x2−x̅2] |
| [x2−x̅2][x1−x̅1] | | [x2−x̅2][x2−x̅2] |
| ⎤
⎥
⎦ | ⟩
|
|
| (67)
|
where angle brackets ⟨⋯⟩ indicate the ensemble
average, and the overbar ⋯ indicates the same thing;
we use two different notations to improve legibility. To say the
same thing another way, we can define the
vector of residuals in terms of its components:
Then to form the covariance matrix, we take the outer product of
Δx(i) with itself, and then take the ensemble average over
all i. That is to say:
|
Σ(x1, x2) | | = | | ⟨Δx(i) ⊗ Δx(i)⟩ |
| | | = | | ⟨Δx(i) Δx(i)T⟩
|
| (69)
|
The superscript T indicates transpose, which in this case
converts a column vector to a row vector.
The generalization to more than two variables is straightforward. The
correlation matrix is guaranteed to be symmetric.
We can simplify things by taking logarithms. Rather than multiplying
G by M⊕ we can add ln(G) to ln(M⊕). The
new variables are:
|
x1 | | := | | ln(G) |
| x2 | | := | | ln(GM) |
| x3 | | := | | ln(M) |
| | | = | | x2 − x1
|
| (70)
|
Also, rather than writing G = A ± B where B is the absolute
uncertainty, we write G = A(1 ± B/A) where B/A is the relative
uncertainty. We will make use of the Taylor expansion,
ln(1+є) = є when є is small.
|
x1 | | = | | x̅1 ± b1 | where | b1 = 1.2×10−4 |
| x2 | | = | | x̅2 ± b2 | where | b2 = 2.01×10−9 |
| x3 | | = | | x̅3 ± b3 | ???
|
| (71)
|
It makes sense to write x1 and x2 in the form of a nominal value
plus an uncertainty, because we think these two quantities are
uncorrelated. They are measured by completely dissimilar methods; G
is measured using a Cavendish balance or something like that, while
GM is measured using clocks and radar to observe the motion of
satellites.
That means the covariance matrix for x1 and x2 is:
Now suppose we wish to change variables. Mass is, after all, directly
relevant to physics. Mass is one of the SI base units. Meanwhile G
is a fundamental universal constant. So let’s choose G and M as
our variables, or equivalently x1 and x3.
|
Σ(x1, x3) | | = | | | |
(73a)
|
| | | = | | ⎡
⎢
⎣ | | 1.43690611443×10−8 | | −1.43690611443×10−8 |
| −1.43690611443×10−8 | | 1.43690611483×10−8
|
| ⎤
⎥
⎦ |
| |
(73b)
|
| | | ☠ | | ⎡
⎢
⎣ | | 1.44×10−8 | | −1.44×10−8 |
| −1.44×10−8 | | 1.44×10−8
|
| ⎤
⎥
⎦ | ☠ |
| |
(73c)
|
|
In the numerical matrix equation 73b, the lower-right matrix
element differs slightly from the others. It differs in the tenth
decimal place.
In equation 73c, we have very unwisely rounded things off to
two decimal places, which is not enough. Even eight decimal places
would not have been enough. Rounding causes the matrix to be
singular. Since we plan on inverting the matrix, this is a Bad Thing.
In fact, even equation 73b is nearly useless, for multiple
reasons. Part of the problem is that the matrix elements are rounded
to machine precision (IEEE double precision), which isn’t really good
enough for this application. That is, you can’t multiply the
numerical matrix by vectors, you can’t invert it, and you can’t find
its eigenvectors or eigenvalues. Anything you try to do runs afoul of
small differences between large numbers. Secondly, even if we could
trust the numbers, it is not humanly possible to look at the numbers
and figure out what they mean.
As a general rule, if you want to extract meaning from a matrix, you
will be much better off if you re-express it using SVD i.e. singular
value decomposition. In our case, we are in luck, because the matrix
is real and symmetric, hence Hermitian, so we can use EVD
i.e. eigenvalue decomposition, which (compared to SVD) is easier to
compute and at least as easy to understand.
Let’s take one preliminary step, to put our matix into form that is
not so numerically ill-conditioned. We start by rotating the matrix
45 degrees:
|
R(−45) Σ(x1, x3) R(45) | | = | | ⎡
⎢
⎣ | | ⎤
⎥
⎦ | Σ(x1, x3) | ⎡
⎢
⎣ | | ⎤
⎥
⎦ |
| |
(74a)
|
| | | = | | ⎡
⎢
⎣ | | 2b12 + b2/2 | | −b22/2 |
| −b22/2 | | b22/2 |
| ⎤
⎥
⎦ |
| |
(74b)
|
| | | = | | ⎡
⎢
⎣ | | 2.8738 | ×10−8 | | −2.0141 | ×10−18 |
| −2.0141 | ×10−18 | | 2.0141 | ×10−18
|
| ⎤
⎥
⎦ |
| |
(74c)
|
|
We can do things with this matrix, without being plagued by small
differences between large numbers. We still have work to do, because
the 45 degree rotation did not exactly diagonalize the matrix.
In general, the power method is a good way to find the
eigenvector associated with the largest eigenvalue. The power method
applied to the inverse matrix will find the eigenvector associated
with the largest eigenvalues of that matrix, which is of course the
smallest eigenvalue of the non-inverted matrix. Also remember that if
you have found N−1 of the eigenvectors, you can construct the last
one using the fact that it is orthogonal to all the others.
In our example, the eigenvectors of the matrix in
equation 74c are:
These vectors are orthonormal. They may not look normalized, but they
are, as closely as possible within the IEEE double precision
representation, which is close enough for present purposes.
We can arrange these side-by-side to define a unitary matrix
|
U | | := | | ⎡
⎢
⎣ | | 1 | 7.00835×10−11 |
| −7.00835×10−11 | 1 |
| ⎤
⎥
⎦ |
|
| (76)
|
This can be thought of as a rotation matrix, with
a rather small rotation angle. We use it to
rotate the covariance matrix a little bit more.
We also make use of the fact that rotation matrices
are unitary, which means R(−θ) = RT(θ) =
R−1(θ).
|
A | | := | | U−1R−1(45) Σ(x1, x3) R(45) U |
| | | = | | ⎡
⎢
⎣ | | 2.8738 | ×10−8 | | 0 |
| 0 | | | 2.0141 | ×10−18
|
| ⎤
⎥
⎦ |
|
| (77)
|
which is diagonal. The matrix elements are the eigenvalues of the
covariance matrix.
To say the same thing the other way, we can write:
|
Σ(x1, x3) | | = | | U R(45) A RT(45) UT | |
(78a)
|
| | | = | | V A VT | |
(78b)
|
| where V | | := | | R(45) U | |
(78c)
|
|
where A is a diagonal matrix of eigenvalues, and V is the
matrix of eigenvectors of the original covariance matrix.
Equation 78b is the standard way of writing the singular
value decomposition, and in this case also the eigenvalue
decomposition.
In the SVD representation, it is exceedingly easy to find the inverse
covariance matrix:
where V is the same as in equation 78c, and we can invert
the diagonal elements of A one by one:
|
A−1 | | = | | | = | ⎡
⎢
⎣ | | 3.4797 | ×107 | | 0 |
| 0 | | | 4.9651 | ×1017
|
| ⎤
⎥
⎦ |
|
| (80)
|
The fact that we could so easily invert the covariance matrix gives
you some idea of the power of SVD.
In general, the inverse covariance matrix is quite useful. For
instance, this is what you use for weighting the data when doing a
least-squares fit. Specifically: In terms of the residuals as defined
by equation 68, the unweighted sum-of-squares is given
by the dot product Δx(i)T Δx(i), whereas the
properly weighted sum is:
which is known as the Mahalanobis distance.
It pays to look at the eigenvalues of the covariance matrix and/or the
inverse covariance matrix. If all the eigenvalues are comparable in
magnitude, it means the correlations are not particularly significant.
Conversely, if some eigenvalues are very much smaller or larger than
others, it means that the correlations are very significant. You can
visualize this in terms of a highly elongated error ellipsoid, as
illustrated in figure 46.
In the example we are considering, one of the eigenvalues is ten
orders of magnitude larger than the other. This helps us to
understand why the matrix in equation 73 is so
ill-conditioned. If we wrote out the inverse covariance matrix
explicitly (without SVD) it would be equally ill-conditioned.
It also pays to look at the eigenvectors.
|
We refer to an eigenvector of the inverse covariance matrix
Σ−1 as being “cheap” or “expensive” according to whether
the associated eigenvalue is small or large.
|
|
The same vectors are
eigenvectors of the plain old covariance matrix Σ, in which
case the cheap eigenvectors have a large eigenvalue (long error bars)
and the expensive eigenvectors have a small eigenvalue (short error
bars).
|
The idea is that in figure 46, if you move away from
the center in an expensive direction (in the direction of the yellow
line), the Mahalanobis distance goes up rapidly, whereas if you move
in a cheap direction (perpendicular to the yellow line), the
Mahalanobis distance goes up only slowly.
This tells us something about the physics. If you just look at the
variance, it tells you that in some sense G is not well determined,
but that does not mean you can cheaply vary the value of G all by
itself. If you don’t want a big penalty, you have to vary G and
vary M⊕ at the same time, in opposite directions, so as to move
along a contour of constant GM⊕.
9.5 Example: Mass and Gravitation (II)
The example presented in section 9.3 was simplified
for pedagogical reasons. In real-world situations, there are
usually many more variables to worry about. For example:
|
G | | = | | | ×10−11 m3kg−1s−2 | |
(82a)
|
| Sun: GM⊙ | | = | | ⎛
⎜
⎝ | | | 1.32712442099 |
| ± | 0.00000000010 |
| ⎞
⎟
⎠ |
| ×1020 kg3s−2 | |
(82b)
|
| Earth: GM⊕ | | = | | ⎛
⎜
⎝ | | | 3.9860044180 |
| ± | 0.0000000080
|
| ⎞
⎟
⎠ |
| ×1014 kg3s−2 | |
(82c)
|
| Moon: GM☽ | | = | | | ×1012 kg3s−2 | |
(82d)
|
| M⊙ | | = | | | ×1030 kg | |
(82e)
|
| M⊕ | | = | | | ×1024 kg | |
(82f)
|
| M☽ | | = | | | ×1022 kg | |
(82g)
|
|
The uncertainties indicated in equation 82e,
equation 82f, and equation 82g take into
account only the associated variance, without regard to any of the
covariances. The trailing digits in the nominal values are necessary
for some purposes, including forming products such as GM⊕ and
ratios such as M⊕/M⊙.
If we choose G and the three masses as our variables, the covariance
will be a 4×4 matrix, with lots of nontrivial correlations.
10 “Correctness” versus Agreement
10.1 Your Data is Your Data
In classroom settings, people often get the idea that the goal is to
report an uncertainty that reflects the difference between the
measured value and the “correct” value. That idea certainly doesn’t
work in real life – if you knew the “correct” value you wouldn’t need
to make measurements.
In all cases – in the classroom and in real life – you need to
determine the uncertainty of your measurement by scrutinizing
your measurement procedures and your analysis.
Given two quantities, you can judge how well they agree.
For example, we say the quantities 10±2 and 11±2 agree
reasonably well. That is because there is considerable overlap
between the probability distributions. It is more-or-less equivalent
to say that the two distributions are reasonably consistent.
As a counterexample, 10±.2 does not agree with 11±.2,
because there is virtually no overlap between the distributions.
If your results disagree with well-established results, you should
comment on this, but you must not fudge your data to improve the
agreement. You must start by reporting your nominal value and
your uncertainty independently of other people’s values. As an
optional later step, you might also report a “unified” value
resulting from combining your results with others, but this must be
clearly labeled as such, and in no way relieves you of your
responsibility to report your data “cleanly”. The reason for this
is the same as before: There is always the possibility that the your
value is better than the “established” value. You can tell whether
they agree or not, but you cannot really tell which (if either) of them
is correct.
Of course, if a beginner measures the charge of the electron and gets
an answer that is wildly inconsistent with the established value, it
is overwhelmingly likely that the beginner has made a mistake as to
the value and/or the uncertainty. Be that as it may, the honorable
way to proceed is to report the data “as is”, without fudging it.
Disagreement with established results might motivate you to go back
and scrutinize the measurement process and the analysis, looking for
errors. That is generally considered acceptable, and seems harmless,
but actually it is somewhat risky, because it means that answers that
agree with expectations will receive less scrutiny than answers that
don’t.
The historical record contains bad examples as well as good examples.
Sometimes people who could have made an important discovery talked
themselves out of it by fudging their data to agree with expectations.
However, on other occasions people have done the right thing.
As J.W.S. Rayleigh put it in reference 30:
One’s instinct at first is to try to get rid of a
discrepancy, but I believe that experience shows such an endeavour
to be a mistake. What one ought to do is to magnify a small
discrepancy with a view to finding out the explanation....
When Rayleigh found a tiny discrepancy in his own data on the molar
mass of nitrogen, he did not cover it up. He called attention to it,
magnified it, and clarified it. The discrepancy was real, and led to
the discovery of argon, for which he won the Nobel Prize in 1904.
Whenever possible, raw data should be taken “blind”, i.e. by someone
who doesn’t know what the expected answer is, to eliminate the
temptation to fudge the data. This is often relatively easy to
arrange, for instance by applying a scale factor or baseline-shift
that is recorded in the lab book but not told to the observer.
Bottom line: Your data is your data. The other guy’s data is the
other guy’s data. You should discuss whether your data agrees with
the other guy’s data, but you should not fudge your data to improve
the agreement.
10.2 Measurement Errors versus Modeling Errors
You should not assume that all the world’s errors are due
to imperfect measurements.
Consider the situation where we are measuring the properties of, say,
a real spring. Not some fairy-tale ideal spring, but a real spring.
It will exhibit some nonlinear force-versus-extension relationship.
Now suppose that we do a really good job of measuring this
relationship. The data is reproducible within some ultra-tiny
uncertainty. For all practical purposes, the data is exact.
Next, suppose we want to model this data. Modeling is an important
scientific activity. We can model the data using a straight line. We
can also model it using an Nth-order polynomial. No matter what we
do, there will always be some “error”. This is an error in the model,
not in the observed data. It will lead to errors in whatever
predictions we make with the model.
Proper error analysis will tell us bounds on the errors of the predictions.
Is this an example of “if it doesn’t work, it’s physics”? No! An
inexact prediction is often tremendously valuable. An approximate
prediction is a lot better than no prediction.
I mention this because far too many intro-level science books seem to
describe a fairy-tale axiomatic world where the theorists are always
right and the experimentalists are always wrong. Phooey!
It is very important to realize that error analysis is not
limited to hunting for errors in the data. In the above example, the
data is essentially exact. The spring is not “at fault” for not
adhering to Hooke’s so-called law. Instead, the reality is that
Hooke’s law is imperfect, in that it does not fully model the
complexities of real springs.
A huge part of real-world physics (and indeed a huge part of real life in
general) depends on making approximations, which includes finding and using
phenomenological relationships. The thing that sets the big leagues apart
from the bush leagues is the ability to make controlled approximations.
11 Samples, Sets, Groups, or Clusters of Observations
11.1 Particles and Clusters
When dealing with sets or clusters of measurements, we
must deal with several different probability distributions at once,
which requires a modicum of care. The conventional terminology in
this area is a mess, so I will use some colorful but
nonstandard terminology.
-
- a) We can consider one individual measurement. You can think
of this as a “particle”.
- b) We can consider a “cluster” of N particular
measurements, i.e. a cluster of particles.
- c) We have the underlying distribution U from which particles
are drawn.
- d) We can consider the derived distribution V from which
clusters are drawn. Note that V is derived from U.
This gives us two equivalent ways of forming a cluster: We can draw a
cluster directly from V, or we can draw N particles from U and
then group them to form a cluster.
Therefore:
-
- a) The ith particle drawn from U is associated
with a measured value xi.
- b) The jth cluster drawn from V is associated with a value
yj formed by taking the cluster mean. For any given
cluster, this is not an estimated quantity; we calculate it exactly
by averaging the N particles in the cluster. See reference 2 for a careful definition of mean, variance, and
standard deviation.
- c) The distribution of particles U has some mean µU and
some standard deviation σU, which we might never know
exactly.
- d) The distribution of clusters V has some mean µV and
some standard deviation σV, which we might never know
exactly. In principle there is a distinction between a distribution
of clusters and a distribution of y-values, but since each cluster
has a y-value, we choose to blur this distinction.
- e) We can estimate µU based on one particular measurement.
- f) We can estimate µU based on a cluster of N measurements.
- g) We cannot estimate σU from one particular measurement.
- h) We can estimate σU from one multi-particle cluster.
See also the definition(s) of sample mean and sample standard deviation
in section 11.4.
Linearity guarantees that µV will always be equal to µU. In
contrast, the definition of σ is nonlinear, and σV will
be smaller than σU by a factor of √N, where N is
the number of particles per cluster. And thereby hangs a tale: all
too commonly people talk about “the” standard deviation, and
sometimes it is hard to figure out whether they are talking about
σU or σV.
Given a single cluster consisting of N measurements, we can form an
estimate (denoted µU′) of the center (µU) of the underlying
distribution. In fact, for a well-behaved distribution, we can set
µU′ = y = ⟨x⟩C, i.e. we can let the y-value of
the cluster serve as our estimate of µU. Meanwhile, we can also
form an estimate (σU′) of the width (σU) of the
underlying distribution, as discussed below.
Given a group consisting of M clusters, we can form an
estimate (µV′) of the center of the distribution of y-values.
Similarly we can form an estimate (σV′) of the width of the
distribution of y-values.
To say the same things more formally:
|
µU | | = | | ⟨x⟩U | | (average over all particles)s |
| yj | | = | | ⟨x⟩Cj | | (average over the jth cluster) |
| µV | | = | | ⟨y⟩V | | (average over all clusters) |
| µV | | = | | µU
|
| (83)
|
Among other things, we note the following:
-
If we increase N (the number of particles per cluster), there
should not be any systematic drift in µ′ i.e. our estimate of
µU. (The estimate wander around randomly, but should not
systematically drift.)
- If we increase N, there should not be any systematic drift in
σU′ i.e. our estimate of σU.
- If we increase N, there will definitely be a systematic
decrease in σV′ i.e. the uncertainty of our estimate of
σV.
Note: Commonly we use [x] as our σU′ i.e. our estimate of
σU, using the [⋯] notation defined in
section 11.4.
When you report the results of a cluster of measurements,
you have a choice:
-
If you choose to consider the underlying distribution U to be
the object of interest, then you should report your best estimate of
µU and your best estimate of σU. That is, you should
report <x> ± [x] … which happens to be equal to
y ± [x]. This reflects the uncertainty associated with
drawing one more particle from the distribution U.
- If you choose to consider y itself to be the object of
interest, then you should report your best estimate of y and the
uncertainty of this estimate. That is, you should report y ±
[y]. This reflects the uncertainty associated with
reproducing your entire experiment, i.e. drawing another entire
cluster from the distribution V.
In either case, you should be very explicit about the choice you have
made. If you just report 4.3 ± 2.1 it’s ambiguous, since
[x] differs from [y] by a factor of √N, which
creates the potential for huge errors.
The relationships among the quantities of interest are shown in
figure 47.
11.2 Estimators
Conceptually, [y] would manifest itself in connection with drawing
multiple clusters from the distribution V. However, you have enough
information within a single cluster to calculate [y]. Just divide
[x] by √N.
For a given cluster of data:
⟨x⟩ aka y is our estimate of µU and also of µV.
[x] is our estimate of σU.
[y] = [x]/√N is our estimate of σV.
11.3 Terminology
The field of statistics, like most fields, has its own terminology and
jargon.
Here are some terms where the statistical meaning is ambiguous and/or
differs from the homespun meaning.
- In statistics, a sample is a set of elements,
i.e. the thing we have been calling a cluster. This is a source of
confusion, because non-statisticians commonly use “sample” to
refer to a single element, i.e. the thing we have been calling a
particle. I introduced the term “cluster” specifically to avoid
this confusion.
In statistics, sample mean refers to y = ⟨x⟩,
i.e. the mean of a given sample i.e. a given cluster. This is a
natural consequence of the definition of sample.
- The standard deviation of a sample (aka
sample standard deviation) is ambiguous. It may refer either
to the bias-corrected standard deviation [x], or to the
uncorrected standard deviation [x]b, or possibly even [x]d.
See section 11.4 and reference 31.
In contrast, the standard deviation of a distribution is
unambiguous. That’s because [x] and [x]b converge in the
large-sample limit, and we can draw and arbitrarily-large sample
from the distribution.
- The standard error of a sample is the standard deviation
of the sample means. This inherits the aforementioned ambiguity in
the definition of standard deviation, so the standard error could be
[y], [y]b, or possibly even [y]d. See reference 32.
- One sometimes sees the expression standard error of the
mean which I believe means the same thing as the plain old standard
error. I don’t know whether “of the mean” in this context is
supposed to refer to the mean of the sample or the mean of the
distribution … but I suppose it doesn’t matter; we can just
accept the phrase as jargon and not worry too much about the
etymology.
- An event is a set of outcomes. This usage is
standard in statistics, but is confusing to non-experts since it
conflicts with the homespun usage of the terms.
If an event is a set with only one element, it is called a simple
event; if it contains multiple elements, it is called a compound
event.
To repeat: When dealing with “standard deviation” in connection with
clusters (samples) of size N, there are at least six ideas in
play:
| | | | | [x] | | [x]b | | [x]d |
| | | | | [y] | | [y]b | | [y]d |
| (84)
|
For large N, note that the left-to-right variation is rather small
within each row, but the row-to-row variation is huge.
11.4 Mean, Variance and Standard Deviation
See reference 2 for a careful definition of mean,
variance, and standard deviation.
12 Contributions to the Uncertainty
The modern approach is to use uncertainty as a catch-all term.
I recommend this approach. Sometimes it is useful to separate out
various contributions to the overall uncertainty ... and sometimes
not.
A few common sources of uncertainty include:
-
Thermal noise.
- Quantum noise (aka zero-point motion).
- Statistical fluctuations, e.g. shot noise. See section 12.1
- Calibration errors.
- Readability.
- Roundoff error. See section 12.2.
- Series truncation error. See section 12.3.
The first five items on this list are often present in real-world
measurements, sometimes to a nontrivial and irreducible degree. In
contrast, the last two items are equally applicable to purely
theoretical quantities and to experimentally measured quantities.
Neither readability nor roundoff error are usually considered
“irreducible” sources of experimental error, since they can usually
be reduced by redesigning the experiment.
12.1 Statistical Fluctuations
As an example of statistical fluctuations, suppose you have a tray
containing 1000 coins. You randomize the coins, and count how many
“heads” turn up. Suppose the first time you do the experiment, you observe
x1 = 511, the second time you observe x2 = 493, et cetera.
There are several points we can make about this. First of all, there
is no uncertainty of measurement associated with the individual
observations x1, x2, etc. after they have been carried out.
These are exact counts. On the other hand, if you want to describe
the entire distribution X = {xi} from which such outcomes are
drawn, it has some mean and some standard deviation. Similarly if you
want to predict the outcome of the next observation, there will
be some uncertainty. For fair coins, we expect x = 500±16 based
on theory, so this is not necessarily an “experimental” uncertainty,
unless you want to consider it a Gedanken-experimental uncertainty.
If you do the actual experiment with actual coins, then experimental
uncertainty would be the correct terminology.
See section 13.6 for more on this.
In some contexts (particularly in electronics), the statistical
fluctuations of a counting process go by the name of shot noise.
12.2 Roundoff Error
As an example of roundoff error unrelated to measurement error,
consider rounding off the value of π or the value of 1/81. We
use the notation and concepts discussed in section 8.3.
|
π | | = | | 3.14159265[⁄] |
| π | | = | | 3.14159[⁄] |
| π | | = | | 3.1[⁄] |
| (85)
|
|
1/81 | | = | | .0123[⁄] |
| 1/81 | | = | | .012[⁄] |
| 1/81 | | = | | .01[⁄] |
| (86)
|
The point is that neither π nor 1/81 has any uncertainty of
measurement. In principle they are known exactly, yet when we express
them as a decimal numeral there is always some amount of roundoff
error.
Roundoff error is not statistical. It is not random. See
section 12.4 for more on this.
12.3 Series Truncation Error
Consider the celebrated series expansion
|
exp(x) | | = | | 1 + x + x2/2! + x3/3! + ⋯ |
| exp(x) | | = | | 1 + x + x2/2! + ⋯ |
| exp(x) | | = | | 1 + x + ⋯ |
| (87)
|
This is a power series, in powers of x. That is, the Nth
term of the series is equal to some power of x times some
coefficient.
Note that in a certain sense, the decimal
representation of any number (e.g. equation 85 or
equation 86) can be considered a power series.
The digits in front of the decimal point are a series
in powers of 10, counting right-to-left. Similarly the
digits after the decimal point are a series
in powers of 1/10, counting left-to-right, such that
the contribution from the Nth digit to the overall
number is equal to 1/10N times some coefficient.Similar words apply to other bases, not just base 10.
Base 2, base 8, base 10, and base 16 are all commonly
used in computer science. They are called binary,
octal, decimal, and hexadecimal.
There are many situations in science where it is necessary to use a
truncated series, perhaps because the higher order terms are unknown
in principle, or simply because it would be prohibitively expensive to
evaluate them. Such situations arise in mathematical analysis and in
numerical simulations.
Every time you use a truncated series you introduce some error into
the calculation. In an iterative calculation, such errors can add up,
and can easily reach troublesome levels.
12.4 Ignorance versus Randomness
Starting from equation 87, whenever you truncate the power series
by throwing away second-order and higher terms, you are left with
1+x every time. Therefore the truncation error is (exp(x)−1−x)
every time. This is not random. It is 100% reproducible.
Similarly, as mentioned in section 12.2, whenever you round off
π to five decimal places you get 3.14159 every time. Therefore
the roundoff error is (π − 3.14159) every time. This is not
random. It is 100% reproducible.
As a third example, consider the force F(x) developed by a spring,
as a function of the extension x. We can expand F(x) as a power
series. In accordance with Hooke’s law we expect the second-order and
higher terms to be small, but in the real world they won’t be zero.
And for any given spring, they won’t be random.
The third example is important, because you don’t know what the
truncation error is. This stands in contrast to the previous two
examples, in the sense that even if you don’t know the value of (π
− 3.14159) at the moment, you could figure it out.
So now we come to the point of this section: If you don’t know the
value of y at the moment, that doesn’t mean y is random. Even if
you don’t know y and cannot possibly figure it out, that does not
mean it is random. More importantly, even if y contains “some”
amount of randomness, that does not mean that successive observations
of y drawn from some distribution Y will be uncorrelated.
|
Ignorance is not the same as randomness.
|
|
|
|
This is important because many of the statistical methods that people
like to use are based on the assumption that the observations are
statistically independent.
- Roundoff errors are generally not random. If you assume they
are statistically independent, you are likely to get spectacularly
wrong answers. See e.g. section 7.12.
- Series truncation errors are generally not random. If you
assume they are statistically independent, you are likely to get
spectacularly wrong answers.
13 Categories of Uncertainty – and Related Notions
In Appendix D of TN1297 (reference 10) you can find a
discussion of some commonly-encountered terms for various
contributions to the overall uncertainty, and various related notions.
I will now say a few words say about some of these terms.
13.1 Tolerance
A tolerance serves somewhat as the mirror image of uncertainty
of measurement. Tolerances commonly appear in recipes, blueprints, and
other specifications. They are used to specify the properties of some
manufactured (or about-to-be manufactured) object. Each number on the
specification will have
some stated tolerance; for example in the expression e.g. 5.000 ±
.003 the tolerance is ± .003. The corresponding property of the
finished object is required to be within the stated tolerance-band; in
this example, greater than 4.997 and less than 5.003.
The idea of tolerance applies to a process of going from numbers to
objects. This is the mirror image of a typical scientific
observation, which goes from objects to numbers.
The notation is somewhat ambiguous, since tolerance is expressed using
exactly the same notation as used to express the uncertainty of a
measurement. The notations are the same, but the concepts are very
different. There are at least three possibilities:
- The widget specification calls for a length of 1±0.010
inches. The uncertainty here is called the tolerance.
- The 17th widget has a length of 1±0.0005 inches. The
uncertainty here reflects how accurately this widget was measured.
- The set of widgets manufactured today has a length of
1±0.004 inches. The uncertainty here is dominated by the scatter
that arises because not all widgets are the same.
This illustrates a subtle but important conceptual point: Whenever you
are talking about a cooked data blob or any other probability
distribution, it is important to ascertain what is the ensemble.
Note the contrast:
|
If the ensemble consists of measuring the 17th widget over
and over again, the uncertainty is the uncertainty of the measurement
process,
0.0005 inches.
|
|
If the ensemble consists of measuring every widget
in today’s production run, the uncertainty is dominated by the
widget-to-widget variability, 0.004 inches. (The uncertainty of
the measurement process makes some contribution, but it is small by
comparison.)
|
When specifying tolerances, the recommended practice is to explain in
words what you want. That is, very commonly the desired result cannot
be expressed in terms of simple “A±B” terminology. For
example, I might walk into the machine shop and say that I would like
a chunk of copper one inch in diameter and one inch long. The
machinists could machine me something 1±0.0001 inches in diameter
and 1±0.0001 inches long, but that’s not what I want; I don’t
want them to machine it at all. In this context they know I just want
a chunk of raw material. In all likelihood they will reach into the
scrap bin and pull out a piece of stock and toss it to me. The
diameter is roughly 1 inch but it’s out-of-round by at least 0.010
inches. The length is somewhere between 1 inch and 6 inches. This is
at least ten thousand times less accuracy than the shop is capable of,
but it is within tolerances and is entirely appropriate. They know
that at the end of the day I will have turned the material into a set
of things all very much smaller than what I started with, so the size
of the raw material is not important.
As another example, a surface-science experiment might require a
cylinder very roughly one inch in diameter and very roughly one inch
long, with one face polished flat within a few millionths of an inch.
It is also quite common to have correlated tolerances. (This is
roughly the mirror image of the correlated uncertainties of
measurement discussed in section 7.16.) For example, I might
tell the shop that I need some spacers one inch in diameter and one
inch long. I explain that since they are spacers, on each cylinder
the ends need to be flat and parallel ... but I’m not worried about
the diameter and I’m not even worried about the length, so long as all
three spacers have the same length ±0.001 inch. That is, the
lengths can be highly variable so long as they are closely correlated.
A common yet troublesome example of correlated uncertainties concerns
the proverbial round peg in a round hole. To a first approximation,
you don’t care about the diameter of the peg or the diameter of the
hole, provided the peg fits into the hole with the proper amount of
clearance. The amount of clearance is the proverbial small difference
between large numbers, which means that the relative uncertainty in
the clearance will be orders of magnitude larger than the relative
uncertainty in the diameters. For a one-of-a-kind apparatus you can
customize one of the diameters to give the desired clearance
... whereas in a mass-production situation controlling the clearance
might require very tight tolerances on both of the diameters. In some
cases you’d be better off using a tapered pin in a tapered hole, or
using a sellock pin (aka spring pin).
13.2 Precision
Nowadays experts generally avoid using the term “precision” except
in a vague, not-very-technical sense, and concentrate instead on
quantifying the uncertainty.
Multiple conflicting meanings of “precision” can be found in the
literature.
One rather common meaning corresponds roughly to “an empirical
estimate of the scatter”. That is, suppose we have a set of
data that is empirically well described by a probability distribution
with a half-width of 0.001; we say that data has a precision of 0.001.
Alas that turns the commonsense meaning of precision on its head; it
would be more logical to call the half-width the imprecision, because
a narrow distribution is more precise.
For more discussion of empirical estimates of uncertainty, see
section 13.6.
It is amusing to note that Appendix D of TN1297 (reference 10)
pointedly declines to say what precision is, “because of the
many definitions that exist for this word”. Apparently
“precision” cannot be defined precisely.
Similarly, it says that accuracy is a “qualitative concept”.
Apparently “accuracy” cannot be defined accurately.
This is particularly amusing because non-experts commonly make a big
fuss about the distinction between accuracy and precision.
A better strategy is to talk about the overall uncertainty
versus an empirical estimate of the scatter, as discussed in
section 13.6.
For another discussion of terminology, see reference 33.
13.3 Accuracy
The term “accuracy” suffers from multiple inconsistent
definitions.
One of the most-common meanings is as a general-purpose
antonym for uncertainty. Nowadays experts by-and-large use
“accuracy” only in an informal sense. For careful work,
they focus on quantifying the uncertainty. For more on this,
see section 13.6.
It is neither necessary nor possible to draw a sharp distinction
between accuracy and precision, as discussed in section 13.2
and section 13.6.
13.4 Readability and Reproducibility
On a digital instrument, there are only so-many digits. That
introduces some irreducible amount of roundoff error into the reading.
This is one contribution to the uncertainty.
A burette is commonly used as an almost-digital instrument, because of
the discreteness of the drops. Drop formation introduces quantization
error.
On an analog instrument, sometimes you have the opportunity to
interpolate between the smallest graduations on the scale. This
reduces the roundoff error, but introduces other types of uncertainty,
due to the vagaries of human perception. You also have to ask whether
you should just replace it with an instrument with finer graduations.
As another example, suppose you are determining the endpoint of a
titration by watching a color-change. This suffers from the vagaries
of human perception. Often, determining the color-change point is the
dominant source of uncertainty; interpolating between graduations on
the burette won’t help, and using a more finely graduated burette
won’t help. In this case, if more resolution is needed, you might
consider using a photometer to quantify the color change, and if
necessary use curve fitting to make best use of the photometer data.
On a digital instrument, the number of digits does not necessarily
dictate the readability or the resolution. This is obvious in the
case where there is autoranging or manual range-switching going on.
Also, I have a scale where the lowest-order digit counts by twos.
I’m not quite sure why; it makes the data “look” less uncertain
(i.e. more reproducible) at the cost of making it actually more
uncertain (i.e. more roundoff error). In any case, the
fact remains: the number of digits does not control the resolution.
The ultimate limit – the fundamental limit – to readability
is noise. If the reading is hopping around all over the place,
roundoff error is not the dominant contribution to the noise.
Interpolating and/or using a finer scale won’t help.
13.5 Systematic versus Non-Systematic Uncertainty
Roughly speaking, uncertainties can be classified as follows:
|
Non-systematic uncertainties are random, with a well-behaved
distribution, and will average out if you take enough
data.
|
|
Systematic biases don’t average out.
|
|
This classification leaves open a nasty gray area
when there are random errors that don’t average out, as
discussed below. This is a longstanding problem with the
terminology, and with the underlying concepts.
|
For example: An instrument with a lousy temperature coefficient might
be reproducible from minute to minute but not reproducible
from season to season.
As another example: Suppose you measure something using an instrument
that is miscalibrated, and the miscalibration is large compared to the
empirical scatter that you see in your readings. As far as anybody
can tell, today, your results are reproducible, because there is no
scatter in the data … yet next month we may learn that your
colleagues – using a different instrument – are not able to
reproduce your results. An example of this is discussed in
section 6.5.
On the third hand, if you kept all the raw data, you might
be able to go back and recalibrate the data without having
to repeat the experiment.
This illustrates a number of points:
-
Scatter (i.e. lack of reproducibility) is not the
only contribution to the uncertainty.
- You should keep all the raw data.
- When you write down a number, you quite commonly
do not know how uncertain it is. You might not know
the actual uncertainty until months or years later.
Indeed, the uncertainty is likely to change from month
to month, depending
on what calibrations etc. are applied.
- The notion of “significant digits” would automatically
associate an uncertainty with every number that you write down,
and therefore would utterly fail to represent the truth of the matter.
So the question is, how do we describe this situation?
The fundamental issue is that there are multiple contributions to
the uncertainty. As usual, it should be possible to describe this in
statistical terms.
We are in some formal sense “uncertain” as to how well your
instrument is calibrated, and we would like to quantify that
uncertainty. There is, at least in theory, an ensemble of
instruments, some of which are calibrated, and some of which are
miscalibrated in various ways, with a horribly abnormal distribution
of errors. Your instrument represents an example drawn from this
ensemble. Since you have drawn only one example, you have no
empirical way of estimating the properties of this ensemble. So we’ve
got a nasty problem. There is no convenient empirical method for
quantifying how much overall uncertainty attaches to your results.
When we take a larger view, the situation becomes slightly clearer.
Your colleagues have drawn additional examples from the ensemble of
instruments, so there might be a chance of empirically estimating the
distribution of miscalibrations.
However, the empirical approach will never be entirely satisfactory,
because even including the colleagues, a too-small sample has been
drawn from the ensemble of instruments. If there is any nontrivial
chance that your instrument is significantly miscalibrated, you should
recalibrate it against a primary standard, or against some
more-reliable secondary standard. For instance, if you are worried
that your meter stick isn’t really 1m long, take it to a machine shop.
Nowadays they have laser interferometers on the beds of the milling
machines, so you can reduce the uncertainty about your stick far
beyond what is needed for typical purposes.
The smart way to proceed is to develop a good estimate of the
reliability of the instrument, based on considerations such as how the
instrument is constructed, whether two instruments are likely to fail
in the same way, et cetera. This requires thought and effort, far
beyond a simple histogram or scatter-plot of the data.
Also keep in mind that sometimes it is possible to redesign the whole
experiment to measure a dimensionless ratio, so that calibration
factors drop out. As a famous example, the ratio of
(moon mass)/(earth mass) is known vastly better than either mass
separately. (The uncertainty of any measurement of either individual
mass would be dominated by the uncertainty in Newton’s constant of
universal gravitation.)
It is possible to make an empirical measurement of the scatter in your
data, perhaps by making a histogram of your data and measuring the
width. However, the point remains that this provides only a lower
bound on the true uncertainty of your results. This may be a tight
lower bound, or it may be a serious underestimate of the true
uncertainty. You can get into trouble if there are uncontrolled
variables that don’t show up in the histogram. This can happen if you
have inadvertently drawn a too-small sample of some variables.
Also beware that “random” errors may or may not average out.
Consider
the contrast:
|
There is a category of random errors that will average out,
if you take enough data.
|
|
There is a category of random errors that
will never average out, no matter how much data you take.
|
|
If your measuring instrument has an offset, and the offset is
undergoing an unbiased random walk, then we can invoke the central
limit theorem to convince ourselves that the average of many
measurements will converge to the right answer.
|
|
If the offset in your
measuring process is undergoing a biased random walk, there
will be an overall rate of drift, and the longer you sit there taking
measurements the more the drift will accumulate. You may have seen an
example of this in high-school chemistry class, when you tried to
weigh a hygroscopic substance.
|
|
|
|
Bias is not the only type of badly-behaved randomness.
Consider for example 1/f noise (“pink noise”), which will never
average out, even though it is not biased, as discussed in
reference 34. (The statement of the central limit theorem has
some important provisos, which are not satisfied in the case of
1/f noise.)
|
|
Averaging can be considered a simple type of digital filter,
namely a boxcar filter. Long-time averaging results in a filter with
a narrow bandwidth, centered at zero. White noise has a constant
power per unit bandwidth, so decreasing the bandwidth decreases the
amount of noise that gets through.
|
|
As the name suggests, 1/f noise
has an exceedingly large amount of noise power per unit bandwidth at
low frequencies. A narrow filter centered at zero is never going to
make the noise average out. You might be able to solve the problem by
using a more sophisticated filter, namely a narrow-band filter
not centered at zero. Hint: lock-in amplifier.
|
Given any set of data, we can calculate the standard deviation of that
data, as mentioned in section 13.2. This is a completely
cut-and-dried mathematical operation on the empirical data. It gives
a measure of the scatter in the data.
Things become much less clear when we try to make predictions based on
the observed scatter. It would be nice if we could predict how well
our data will agree with future measurements of the same quantity
... but this is not always possible, and is never cut-and-dried,
because there may be sources of uncertainty that don’t show up in the
scatter.
Note that what we have been calling “scatter” is
conventionally called the “statistical” uncertainty. Alas, that
is at best an idiomatic expression, and at worst a misleading
misnomer, for the simple reason that virtually anything can be
considered “statistical” in the following sense: Even absolute
truth is statistical, equivalent to 100% probability of
correctness, while falsity is statistical, equivalent to 0%
probability of correctness.It might be slightly better to call it an empirical estimate
or even better an internal estimate of one contribution to
the uncertainty. The informal term scatter is as good as
any. However, even this is imperfect, for reasons we now
discuss:
Niels Bohr once said “Never express yourself more clearly than
you are able to think”. By that argument, it is not worth
coming up with a super-precise name for the distinction between
scatter and systematic bias, because it is not a super-precise
concept. It depends on the details of how the experiment is done.
Suppose we have a set of voltmeters with some uncertainty due to
calibration errors. Further suppose one group measures something
using an ensemble of voltmeters, while a second group uses only a
single voltmeter. Then calibration errors will show up as
readily-observable scatter in the first group’s results but will
show up as a hard-to-detect systematic bias (not scatter) in the
second group’s results.
An oversimplified view of the relationship between scatter and
systematic bias is presented in figure 48. In all four
parts of the figure, the black data points are essentially the same,
except for scaling and/or shifting. Specifically: In the bottom row
the spacing between points is 3X larger than the spacing in the top
row, and in the right-hand column the pattern is off-center,
i.e. shifted to the right relative to where it was in the left-hand
column.
The data is a 300-point sample drawn from a two-dimensional Gaussian
distribution. That is, the density of points falls of exponentially
as a function of the square of the distance from the center of the
pattern.
Figure 48 is misleading because it suggests that you can
with one glance estimate how much the centroid suffers from
systematic bias. In contrast, in the real world, it is very very
hard to get a decent estimate of this. You can’t tell at a glance how
far the data is from the target, because you don’t know where the
target is. (If you knew the location of the target, you wouldn’t have
needed to take data.) The real-world situation is more like
figure 49.
Remark: Some terminological equivalences are presented in the
following table. It is, alas, hard to quantify these terms, as
discussed in section 13.2 and section 13.3.
| statistics: | | variance | | vs. | | bias |
| lab work: | | random error | | vs. | | systematic error |
| | | low precision | | vs. | | low accuracy |
| hybrid: | | scatter | | vs. | | systematic bias |
Here’s another issue: Sometimes people imagine there is a clean
dichotomy between precision and accuracy, or between scatter and
systematic bias ... but this is not right. Scatter is not the
antonym or the alternative to systematic bias. There can perfectly
well be systematic biases in the scatter!
In particular, moving left-to-right in figure 48
illustrates a systematic offset of the centroid. In contrast,
moving top-to-bottom in figure 48 illustrates a systematic
3x increase of the standard deviation.
Here’s how such issues can arise in practice: Suppose you want to
measure the Brownian motion of a small particle. If the raw data is
position, then the mean position is meaningless and the scatter in the
data tells you everything you need to know. If you inadvertently use
a 10x microscope when you think you are using a 30x microscope, that
systematically decreases the scatter by a factor of 3.
This is a disaster, because it introduces a 3x systematic
error in the main thing you are trying to measure.
As another example in the same vein, imagine you want to measure the
noise figure of a radio-frequency preamplifier. The raw data is
voltage. The mean of the data is meaningless, and is zero by
construction in an AC-coupled amplifier. The scatter in the data
tells you everything you need to know.
On the other hand, in the last two examples, it might be more
practical to shift attention away from the raw data to a slightly
cooked (“parboiled”) representation of the data. In the Brownian
motion experiment, let the parboiled data be the diffusion constant,
i.e. the slope of the curve when you plot the square of the distance
traveled versus time. Then we can talk about the mean and standard
deviation of the measured diffusion constant.
Here’s a two-part constructive suggestion:
- Remember that a cooked data blob is not a plain number; it is a
probability distribution. Analyzing such things means adding,
subtracting, multiplying, dividing, and comparing different
probability distributions.
- To describe a simple theoretical probability distribution such
as a Gaussian, you need two numbers: The mean and standard deviation.
Both numbers are important! Two distributions with the same mean and
different standard deviations are different distributions, as
illustrated by the green and black curves in figure 50.
You need both the mean and the standard deviation. You should avoid
and/or account for systematic biases in both numbers, not one or the
other. (For more complicated distributions, there is even more to
worry about.)
Scatter is one contribution to our uncertainty about the nominal
value. The measured scatter provides a lower bound on the
uncertainty. It tells you nothing about possible systematic offsets
of the nominal value, and tells you nothing about possible systematic
errors in the amount of scatter itself (as in the microscope example
above).
When reporting the uncertainty, what really matters is the total,
overall uncertainty. Breaking it down into separate contributions
(scatter, systematic bias, or whatever) is often convenient, but is
not a fundamental requirement.
Quantifying the scatter is easy ... much easier than estimating the
systematic biases in the mean and standard deviation. Do your best to
estimate the total, overall uncertainty.
In an introductory class, students may not have the time, resources,
or skill required to do a meaningful investigation of possible
systematic biases. This naturally leads to an emphasis on analyzing
the scatter ... but this emphasis should not become an overemphasis.
Remember, the scatter is a lower bound on the uncertainty, and
should be reported as such. There is nothing wrong with saying “We
observed σX to be such-and-such. This provides a lower bound
on the uncertainty of ⟨X⟩. There was no investigation
of possible systematic biases”.
|
The scatter provides a lower bound on the uncertainty.
|
|
|
|
Remark: Notation: Sometimes you see a measurement reported using an
expression of the form A±B±C, where A is the nominal
value, B is the observed scatter, and C is an estimate of the
systematic bias of the centroid. This notation is not very well
established, so if you’re going to use it you should be careful to
explain what you mean by it.
13.7 “Experimental Error”
The title of this section is in scare quotes, because you should be
very wary of using the term “experimental error”. The term has
a couple of different meanings, which would be bad enough ... but then
each meaning has problems of its own.
By way of background, note that the word “error” has the same
ancient roots as the word “errand” or “knight errant”, referring
to wanderings and excursions, including ordinary, normal,
and even commendable excursions.
However, for thousands of years, the word “error” has also denoted
faults, mistakes, or even deceptions, which are all undesirable,
reprehensible things that “should” have been avoided.
Sometimes the term “experimental error” is applied to unavoidable
statistical fluctuations, and sometimes it is applied to avoidable
mistakes and blunders. These two meanings are dramatically different.
They are both problematic, but for different reasons:
- Statistical fluctuations (as discussed in section 12.1
and section 13.6) must not be considered mistakes or blunders.
It is better to call them noise, excursions, or fluctuations – not
errors. Some amount of fluctuation is unavoidable, required by the
laws of physics and/or mathematics. Complaining about statistical
fluctuations makes as much sense as complaining that the square root
of two is irrational. The square root of two is irrational because it
has to be. By the same logic, statistical fluctuations are present in
sampling-type experiments because they have to be. In section 12.1, there is nothing “erroneous” – i.e. nothing mistaken
– about the observations x1 = 511, x2 = 493, et cetera.
- If you are talking about mistakes and blunders, it is arguably
possible to categorize them as “experimental error” ... but doing so
would not be very useful. In particular you should not pretend that
mentioning this category is, by itself, a sufficient explanation. It
is only a broad, general category. If you believe a mistake has been
made, you should describe the mistake as specifically as possible,
rather than trying to sweep it under the rug by using vague, catch-all
terminology. For example:
- If you think there is a typographical error in the data, explain
why you think so, and explain how this is expected to affect the results.
- If one of the samples was dropped on the floor and/or
spilled, say so, and explain how this is expected to affect the
results.
- Et cetera.
Consider the contrast:
|
Negative example: Saying “our result differs from the
accepted value by 15% due to experimental error” is not a
explanation. Often graders, reviewers, and/or editors will
automatically reject a report that contains such a statement.
|
|
In contrast, you might get away with using “Experimental Error” as
the headline of a section in which the specific sources of error
were analyzed. Even that is not recommended; a better headline
would be “Sources of Uncertainty” or some such.
|
Last but not least, we should mention that the term “error bar” has
entered the language as an idiomatic expression. Logically it should
be called an “uncertainty bar” but nobody actually says that. So we
will continue to call it an error bar, with the understanding that it
measures uncertainty.
13.8 Other Limits to the Notion of Uncertainty
Beware that you cannot always describe a
distribution in terms of some “nominal value” and some
“uncertainty”. There is a whole litany of things that could go
wrong.
- It may be that you have a mildly skewed distribution, leading to
mildly lopsided error bars. So, rather than writing 400±15% it
might suffice to write something like 400(+10%, −20%). Sometimes
this is sufficient, but sometimes not, depending on the actual form of
the distribution. If the Crank Three Times™ method
gives you lopsided error bars, you need to investigate further,
because it might be a warning that you are operating near a
singularity.
- Sometimes you have a bimodal distribution, such that the typical
values are nowhere near the median value.
- Sometimes you have a multi-dimensional probability distribution.
In such cases, there will almost always be correlations, in which case
you cannot describe the distribution using two numbers per dimension,
even if we restrict attention to Gaussian normal distributions
… except special cases as discussed below.
- It could be even worse than that, as illustrated by
the example in section 7.19.
An example of correlated data is shown in figure 46 as
discussed in section 9.3.
For a moment, let’s restrict attention to Gaussian distributions. In
D dimensions, a Gaussian can be described using a vector with D
components (to describe the center of the distribution) plus a
symmetric D×D matrix (to describe the uncertainties). That
means you need D+D(D+1)/2 numbers to describe the Gaussian.
|
In the special case where the uncertainties are all
uncorrelated, the matrix is diagonal, so we can get by with only 2D
numbers to describe the whole Gaussian, and we recover the simple
description in terms of “nominal value ± uncertainty” for each
dimension separately. Such a description provides us with the 2D
numbers that we
need. Obviously D=1 is a sub-case of the uncorrelated case.
|
|
If the
uncertainties are correlated, we need more than 2D numbers to
describe what is going on. It is impossible in principle to describe
the situation in terms of “nominal value ± uncertainty” because
that only gives us 2D numbers.
|
In the real world, sometimes the uncertainties are uncorrelated, but
sometimes they are not. See section 7.16 and
section 9.3 for examples where correlations must be
taken into account. See section 7.16 for an example of how you
can handle correlated data.
Also, beware that not everything is Gaussian. Other distributions –
including square, triangular, and Lorentzian among others – can be
described using using two parameters, and represented using the
“value” ± “uncertainty” notation. More-complicated distributions may
require more than two parameters.
If you know that your data has correlations or has a non-normal
distribution, be sure to say so explicitly.
14 Significance
14.1 Significant ≡ Worth Knowing
The significance of data depends on how the data is being used. Value
judgments are involved. Let’s start by examining some examples.
- I buy a pound of beans, it may contain a great number of small
beans, or a lesser number of larger beans. If desired, I could
determine the number of beans with essentially zero uncertainty, simply
by counting. However, if I just intend to cook and eat the beans, the
cost of counting them far exceeds the value of knowing the count. The
total mass is more significant than the count (unless the count is
wildly large or wildly small).
- Suppose a market-maker (such as a broker) sets the price of
beans at 100 dollars per ton, and identifies a buyer and a seller. To
the seller, the most significant feature of this data is that the
price is above 80, because that allows him to make a profit. To the
buyer, the most significant feature of this data is that the price is
below 120, which allows him to make a profit.
Of course the most significant feature of the data is usually
not the only significant feature of the data.
- When driving in good weather on a deserted highway, the posted
speed limit is a significant factor in deciding how fast to drive. On
the other hand, when driving in traffic in dark, rainy, foggy
conditions, the posted speed limit has no immediate significance,
because you are obliged to drive much slower than that.
From this we see that true significance is highly dependent on the
details of the application. In particular, one feature of the data
that might be significant to one user, while another feature is
significant to another user.
All this can be summarized by saying some feature of the data is
significant if and when it is worth knowing. We take this as
our definition of “significance”.
Formerly it some authorities used the term “significance” as a
general-purpose antonym for uncertainty, but nowadays this is
considered a bad idea.
14.2 Users Decide
Generally it is up to each user of the data to decide which
features of the data are significant, and how significant they are.
In contrast, the data-producers generally do not get to decide how
significant it is.
It is, however, important for the data-producers to have an estimate
of the significance, to help guide and motivate the data-production
process. Here’s how it often works in practice: Before attempting to
measure something, you ought to identify one or two significant
applications of the data. This gives you at least a lower bound on
the significance of the measurement. You don’t need to identify all
applications, just enough to convince yourself – and convince the
funding agencies – that the measurement will be worth doing.
Note the distinction: the data-producers do not get to decide the
significance, but they should obtain an estimate (or at least
a lower bound) for the significance.
This explains why in, say, a compendium of fundamental constants,
there is much discussion of uncertainty but almost no mention of
significance.
14.3 Significance versus Uncertainty
Significance is important, and uncertainty is important, but you must
not confuse the two. Significance is not even a category or component
of the uncertainty. (This is in contrast to, say, roundoff error,
which is one component of the overall uncertainty.)
Significance is not the opposite of uncertainty. Uncertainty is not
the opposite of significance. We can see this in the following
examples:
- As mentioned above, “bean counting” is proverbial for having
low significance, despite its low uncertainty.
- At the opposite extreme, data that is highly uncertain may
nevertheless be highly significant. Hidden significance can be
extracted by signal averaging or other data-reduction techniques,
e.g. as demonstrated in section 7.12.
Various combinations of significance and/or uncertainty are summarized
in figure 51.
When only a single scalar is being measured, and only a single
final application is contemplated, it is sometimes tempting to arrange
things so that the uncertainty of the measurement process is well
matched to the inverse of the significance of the final application.
Sometimes that is a good idea, but sometimes not.
In this connection, it must be emphasized that the significant-figures
rules are a very crude way of representing uncertainty. Also,
despite the name, they are not used to
represent significance! This should be obvious from the
fact that the sig-figs rules as set forth in the chemistry textbooks
deal with roundoff error and other sources of uncertainty, which are
under control of the data-producers. The rules say nothing about the
data-users, who always determine the true significance.
The significant-figures rules
do not even attempt
to represent significance.
|
|
|
|
The foregoing remarks apply to the significant-digits rules, not
to the digits themselves. In contrast, if/when we choose to operate
under a completely different set of rules, we can arrange for the
number of of digits to be related to the true significance. A simple
example of this can be found in section 2.1.
Let us now discuss a more interesting example. Suppose we have a
chemical plant that unfortunately releases a certain level L of
pollutants into the air. The government has established a threshold,
and requires that the actual level of pollutants remain below the
threshold.
Let us consider the quantities
|
x | | = | | L − threshold |
| y | | = | | L − threshold + safety margin |
| (88)
|
On a day-to-day basis, from the point of view of the plant supervisor,
the most significant feature of the data is that x remain less than
zero, with high confidence. In many situations it is convenient to
replace this with a statement that our best estimate of y is less
than zero, where y contains a built-in safety margin.
Note that the assertion that y is less than zero is a one-bit binary
statement. The value of y is being expressed using less than one
significant digit.
The error bars on x, y, and L don’t matter so long as they are
short enough, i.e. so long as the distribution on L does not cross
the threshold to any appreciable extent.
The plant supervisor may wish to conceal the true value of L from
competitors. Therefore it may be desirable, when filing reports, to
include only the most severely rounded-off approximation to L.
We have seen multiple reasons why the plant supervisor might find it
convenient to round things off very heavily. This roundoff is based
on true significance, competitive considerations,
and other considerations ... none of which are directly
related to the uncertainty of the measurement. To say the same thing
another way, the significance-based roundoff completely swamps any
uncertainty-based roundoff that you might have done. This
significance-based roundoff is not carried out using the “sig-figs”
rules that you find in the chemistry textbook ... not by a long shot.
This should be obvious from the fact that the sig-figs rules are (at
best) a crude way of expressing uncertainty, not significance. The
fact that extreme significance-based roundoff is possible is not an
excuse for teaching, learning, or using the sig-figs rules.
Meanwhile we must keep in mind that features that are insignificant
for one purpose may be very significant for other purposes.
- First and foremost, if we ever get into a situation where L is
not far below the threshold, the plant supervisor is going to
get very excited. He will call in the operating engineer, and maybe
the design engineer and other folks, and they will all want to know an
accurate value for L and the uncertainty of the distribution from
L was drawn. They will not settle for some crudely rounded-off
version of L.
- The design engineer who is designing an upgrade to the plant
almost certainly wants to know the actual L-value (not rounded-off
approximation to L) and wants to know the actual uncertainty.
- Similarly an epidemiologist who is considering whether to raise or
lower the threshold almost certainly wants to know the L-value and
the uncertainty.
15 Analysis Plus Synthesis – Closing the Loop
Figure 52 shows a rough outline of how people
generally approach data analysis. They start with some raw data.
They perform some analysis, perhaps curve fitting of the sort
described in section 7.24. The curve is a model, or
rather a parameterized family of models, and analysis determines the
parameters. The hope is that the fitted parameters will have some
meaning that promotes understanding.
The parts of the figure shown in gray express an idea that is not
often thought about and even less often carried out in practice,
namely the idea that the model could be used to generate data,
and given the right parameters it could generate data that is in some
ill-specified sense “equivalent” to the data we started with. We
will not pursue this idea, because it’s not the best way to do things.
A better strategy is shown in figure 53. We start
by choosing some parameters that seem plausible, in the right
ballpark. We feed those into the model, to generate some fake data.
We then analyze the fake data using our favorite data-analysis tools.
The reconstructed parameters really ought to agree with the chosen
parameters. This is a valuable check on the validity of the model and
the validity of the analysis methods.
Passing this test is necessary but not sufficient. It is necessary
because if the analyzer cannot handle fake data, it certainly cannot
handle real data. It is not sufficient because sometimes the analyzer
works fine on fake data but fails miserably on real-world data –
perhaps because both the model and the analyzer embody the same
misconceptions.
16 The Definition of Probability
Please see reference 2 for a discussion
of fundamental concepts of probability.
17 More than You Ever Wanted to Know about Sig Figs
17.1 Supposed Goals
The term “significant figures” is equivalent to “significant
digits”. Such terms are commonly encountered in introductory
science books. At last check they were more common in chemistry books
than in physics or biology books. They appear to be gradually
becoming less common overall, which is a good thing.
The meaning of these terms is remarkably muddled and inconsistent.
There are at least three categories of ideas involved. These include:
-
- a) Rounding off.
- b) Attempting to use roundoff to express uncertainty.
- c) Propagating uncertainty from step to step
during calculations.
No matter what goal we are trying to achieve, sig figs are never the
right way to do it. Consider the following contrast between goals and
means, in each of the three categories mentioned above:
|
a) Roundoff: Whenever you write down a number, you
need to write some definite number of digits, so some sort of roundoff
rules are necessary. Basic practical rules for rounding off are given
in section 1.1. In more advanced situations, you can
apply the Crank Three Times™ method (section 7.14)
to each step in the calculation to confirm that you are carrying
enough guard digits.
|
|
The sig fig rules are the wrong roundoff rules.
They require the roundoff to be far too aggressive. There are plenty
of important cases where following the usual “significant figures”
rules would introduce unacceptable and completely unnecessary errors
into the calculations. See section 7.2 and
section 17.4.3 for simple examples of this.
|
|
b) Describing distributions:
Basic practical methods for describing
probability distributions are outlined in
section 1.2. The width of a given distribution can be
interpreted as the uncertainty of that distribution.
|
|
Beware
that roundoff is only one contribution to the overall uncertainty.
One of the fundamental flaws in the sig-figs approach is that it blurs
the distinction between roundoff and uncertainty. This is a serious
blunder. Sometimes roundoff error is the dominant contribution to the
overall uncertainty, but sometimes not. Indeed, in a well-designed
experiment, roundoff error is almost never the dominant
contribution. Furthermore, the sig figs rules do a lousy job of representing the
uncertainty. See section 17.5.2 and section 8.8
for examples where sig figs wildly overstate or wildly understate the
width of the distribution.
|
|
c) Propagation: Often you perform some calculations
on the raw data in order to obtain a result. We need a way of
estimating the uncertainty in the result. Practical methods for doing
this are discussed in section 7.14 and section 7.16.
|
|
The
technique of propagating the uncertainty from step to step throughout
the calculation is a very bad technique. It might sometimes work for
super-simple “textbook” problems but it is unlikely to work for
real-world problems. Commonly propagation works for some steps in a
calculation but not others, and since a chain is only as strong as its
weakest link, the overall calculation fails. See
section 7.20 for additional discussion and examples of
this. Step-by-step propagation does a particularly bad job when
dealing with correlations. It is also quite laborious and
error-prone. This is not intrinsically a sig-figs problem; step-by-step propagation
is a bad idea whether or not the uncertainty is represented by sig
figs. On the other hand, no matter what you are doing, you can always
make it worse by using sig figs.
|
People who care about their data don’t use significant figures.
Anything you might do with sig figs can be done much better
(and more easily!) by other means.
The sig figs method
is needlessly difficult
and gets wrong answers.
|
|
|
|
It is not safe to assume that counting the digits in a numeral implies
anything about the significance, uncertainty, accuracy,
precision, repeatability, readability, resolution, tolerance, or
anything else. See section 17.5.2 for more discussion of this
point, including an example.
On the other hand, beware that some people use the term
“significant figures” as an idiomatic expression, referring to
the topic of uncertainty in the broadest sense ... even though they
would never take the sig figs rules literally. This broad idiomatic
usage is a bad practice because it is likely to be misunderstood,
but we should not assume that every mention
of the term “significant figures” is complete nonsense.
Also beware that the meaning of the term “significant figures”
has changed over the course of history. See
section 17 for various ways the term was used in
times past.
17.2 OK: Sig figs ↔ Place Value
The number 120 can be considered the “same” as 1200 except for place
value. This is useful when multiplying such numbers: we can multiply
12 by 12 and then shift the result three places to obtain 144000.
This has absolutely nothing to do with roundoff or with any kind of
uncertainty. All the numbers mentioned here are exact.
Similar ideas are useful when computing the characteristic (as opposed
to mantissa) of a logarithm. Again this has nothing to do with
roundoff or uncertainty; the characteristic is the same no matter
whether you are using four-place logarithms or seven-place logarithms.
These ideas have been around for hundreds of years. They are
harmless provided you do not confuse them with other ideas,
such as the disastrous ideas discussed in section 17.4.
17.3 Mostly OK: Sig figs ↔ Roundoff
Given a number in scientific notation, if you know it has been rounded
off to a certain number of digits, then you know the magnitude of the
roundoff error distribution.
This idea is OK as far as it goes, but there are several important
caveats:
- You cannot necessarily tell by looking at a number whether it
has been rounded off. For example, the number of centimeters in an
inch is 2.54 exactly; this number has not been rounded off.
- Given a number that is not in scientific notation, you cannot
necessarily tell by looking at it whether it has been rounded off at
all, let alone how much it has been rounded off. For example, the
number 1200 might be an exact integer, or it could be an inexact
quantity rounded off to four digits ... or three digits ... or
two digits.
- Roundoff error is not the same as overall uncertainty.
Sometimes it is the dominant contribution to the overall
uncertainty, but sometimes not. Since roundoff error is
almost always avoidable, in a well designed experiment
it is never the dominant contribution to the uncertainty.
We have a serious problem, because nowadays when most people speak of
“significant figures” they are referring to a set of rules that
require you to keep rounding off until roundoff error is
dominant, or at least comparable to the overall uncertainty.
This is an abomination, as we discuss in section 17.4.
17.4 Abomination: Sig Figs ↔ Uncertainty
17.4.1 If You Mean Place Value, Say Place Value
See section 17.2 and section 18 for a
discussion of the mathematical notion of place value and significance.
17.4.2 Observations versus Distributions
As discussed in section 5 and
section 6.4, there is a crucial distinction between a
distribution and some observation drawn from that
distribution. An expression of the form 12.3±0.5 clearly refers
to a distribution. One problem with the whole idea of significant
figures is that in an expression such as x=12.3, you can’t tell
whether it is meant to describe a particular observation or an entire
distribution over observations. In particular: Does it refer to an
indicated value, or to the entire distribution over true values?
17.4.3 Example of Sig-Figs and Roundoff: Calculating Density
A chemistry teacher once asked 1000 colleagues the
following question:
Consider an experiment to determine the density of some material:
mass = 10.065 g and volume = 9.95 mL
Should the answer be reported as 1.01 g/mL or 1.011 g/mL?
Soon another teacher replied
Maybe I missed something, that's a very straightforward problem.
The answer should be reported as 1.01 g/mL.
The claim was that since one of the givens is only known to three sig
figs, the answer should be reported with only three sig figs, strictly
according to the sig-figs rules.
Shortly thereafter, a third teacher chimed in, disagreeing with the
previous answers and saying that the answer should be reported as
1.011 g/mL. He asserted that the aforementioned
digit-counting rules were «simplistic» and should be discarded in
favor of the concept of relative uncertainty. His final
answer, however, was expressed in terms of sig figs.
Eventually a fourth teacher pointed out that if you do the math
carefully, you find that 1.012 is a better answer than either of
the choices offered in the original question.
Remarkably, none of these responses attached an explicit uncertainty
to the answer. Apparently they all hoped we could estimate uncertainty
using the “sig figs” doctrine. As a result, we don’t know whether
1.01 means 1.01[½] or 1.01(5). That’s distressingly
indefinite.
At this point you may be wondering whether this ambiguity is the whole
problem. Perhaps we should accept all three answers –
1.01[½], 1.011(5), and 1.012(5) – since they are all close
together, within the stated error bars.
Well, sorry, that doesn’t solve the problem. First of all, the
ambiguity is a problem unto itself, and secondly there is a deeper
problem that should not be swept under the rug of ambiguity.
The deeper problem is that if you solve the problem properly – for
instance using the Crank Three Times™ method as
described in section 7.14 – you find it might be reasonable to
report a density of 1.0116(5) g/mL, which is a very different
answer. This is a much better answer. It is represented by the blue
trapezoid in figure 54.
In the previous paragraph, and in the next several paragraphs, we
assume the mass and density started out with a half-count of absolute
uncertainty, such as might result from roundoff. Specifically, if
we do the calculation properly, we have:
|
mass | | = | | 10.065[½] g | : | 5e−5 relative uncertainty |
| volume | | = | | 9.95[½] mL | : | 5e−4 relative uncertainty |
| density | | = | | 1.0116(5) mL | : | 5e−4 relative uncertainty
|
| (89)
|
Note that if we count the significant digits and compare the mass to
the volume, the mass has two digits more. In contrast, in terms
of relative uncertainty, the mass has only one order of
magnitude less. This gross discrepancy between the number of sig figs
and the relative uncertainty is discussed in section 8.6.3. Given that roundoff errors have a peculiar
distribution (as seen in e.g. figure 42),
and given a mass just above 10 and a volume just below 10, you should
expect a fiasco if you try to do this calculation using
significant figures.
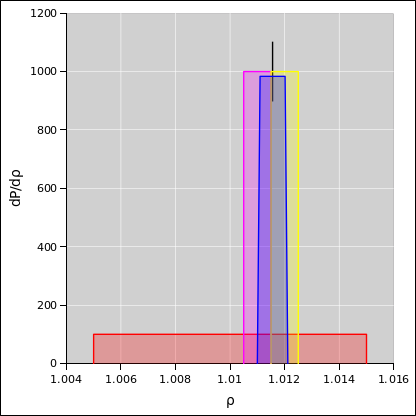 Figure 54
Figure 54: Four Answers to the Density Question
Figure 54 shows the various probability distributions
we are considering. It shows each distribution as a histogram. The
best answer is represented by the blue trapezoid. The center of the
correct distribution is shown by the black line.
- You can see at a glance that the answer based on the sig figs
rules, namely 1.01[½], bears hardly any resemblance to the
correct answer. The distribution is far too spread out, and is not
centered in the right place. This is shown in red in the figure.
- The second answer that was offered was 1.011. If we are
generous and interpret that as 1.011[½], it’s not completely
crazy, but it’s not very good, either. It is shown in magenta in the
figure. Relative to the true center, the alleged center of the
distribution is shifted by more than the HWHM of the distribution, as
you can see in figure 54. (If we are ungenerous and
interpret it as 1.011(5), the result is terrible, as discussed in
item e below.)
- The third answer, namely 1.012, is marginally better, but only
marginally. If we are generous and interpret it as 1.012[½],
the alleged center of the distribution is shifted by slightly less
than the HWHM of the distribution. This is shown in yellow in the
figure. That’s still a substantial degradation.
- Therefore it is much better to report 1.0116(5), as shown in
blue in the figure. This answer complies with the recommendations in
section 8.2: it uses few enough digits to be reasonably convenient,
it uses many enough digits to keep the roundoff errors from causing
problems, and it states the uncertainty separately and explicitly.
Tangential remark: Ths blue distribution is shown as a trapezoid.
That’s a refinement that results from considering the uncertainty of
the mass (not just the uncertainty on the volume). This causes the
distribution of density-values to be slightly more spread out. The
peak is correspondingly slightly lower. In most situations you could
safely ignore this refinement.
- The answers of 1.011(5) and 1.012(5) are just as terrible as
the sig-figs result in item a above. They are not shown explicitly in
the figure, but they would look similar to the aforementioned
1.01[½] as shown in red. We see that appealing to ambiguity
does not even begin to solve the problem.
This example illustrates the following point:
It is fairly common for the smart answer to have
two more digits than the sig-figs answer would have.
|
|
|
|
Additional discussion: It must be emphasized that the original
question was predicated on assuming bad laboratory practice. For
starters, in a well-designed experiment, roundoff error is virtually
never the dominant contribution to the overall uncertainty. As
a partially-related point, there should always be a way of figuring
out the uncertainty that does not depend on significant digits.
At an even more fundamental, conceptual level, it is a mistake to
attribute uncertainty to a single measurement of the mass or volume.
The only way there can be any meaningful concept of uncertainty is if
there is an ensemble of measurements. If you were serious about
measuring the density, you would measure several different samples of
the same material. In such a case, it would be madness to calculate
the mean and standard deviation of the masses and the mean and
standard deviation of the volumes. The rational thing to do would be
to plot all the data in mass-versus-volume space and do some sort of
curve fit to determine the volume. The basic idea is shown
in figure 55.
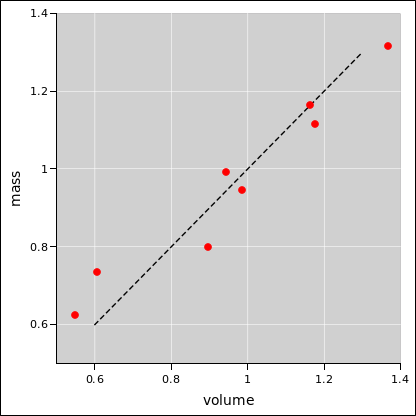 Figure 55
Figure 55: Scatter Plot of Density Measurements
Sig-figs discussion: Sig figs is guaranteed to give the wrong
answer to this question, no matter what version of the sig-figs rules
you apply, if you apply the rules consistently.
- Suppose you adhere to the sig-figs sect that says numbers have a
half-count of uncertainty in the last place. If you apply this rule
consistently to the givens and to the answer, the uncertainty in the
answer is an order of magnitude too big.
- Suppose you adhere to the sig-figs sect that says numbers have a
few counts of uncertainty in the last place. If you apply this rule
consistently to the givens and to the answer, the uncertainty in the
answer is an order of magnitude too big.
The sig-figs rules are not merely ambiguous,
they are self-inconsistent.
|
|
|
|
This sort of fiasco is very likely to occur when one or more of the
numbers is slightly greater than a power of 10, or slightly less. If
you want to get the right answer, you should stay far away from the
sig-figs cesspool.
17.4.4 Uncertainty, Insignificance, and Guard Digits
Recall that uncertainty is not the same as insignificance; see
section 7.12, section 8.8, and
section 12 especially figure 51 in
section 14.
The usual “sig figs rules” cause you to round things off far
too much. If possible, do not round intermediate results at all. If
you must round, keep at least one guard digit.
As an illustration of the harm that “sig figs” can cause, let’s
re-do the calculation in section 7.21. The only difference is
that when we compute the quotient, 11.5136, we round it to two
digits ... since after all it was the result of an operation involving
a two-digit number. That gives us 12, from which we subtract 9.064
to obtain the final “result” ... either 2.9 or 3. Unfortunately
neither of these results is correct. Not even close.
Oddly enough, folks who believe in significant digits typically use
them to represent uncertainty. Hmmmm. If they use significant
digits to represent uncertainty, what kind of digits do they use
to represent significance?
Reference 35 gives additional examples. It summarizes by
saying: “The examples show that the conventional rules of thumb for
propagating significant figures frequently fail.”
17.4.5 Bogus Apology: “Rough Uncertainty”
It is sometimes claimed that the sig-digs rules are only intended
to give a “rough” estimate of the uncertainty. That sort of apology is
crazy and very unhelpful, because even if you believe what it says, it
doesn’t make it OK to use sig figs.
Keep in mind that sig figs cause multiple practical problems and
multiple conceptual problems, as discussed in
section 1.3. Apologizing for the “rough uncertainty”
tends to make people lose sight of all the other problems that sig
figs cause.
Even if we (temporarily!) focus just on the uncertainty, the apology
is often not acceptable, because the so-called “rough” estimate is
just too rough. Even ignoring the sectarian differences discussed in
section 17.5.1, the “sig-digs rules” convey at best only a range
of uncertainties. The top of the range has ten times more uncertainty
than the bottom of the range. If you draw the graph of two
distributions, one of which is tenfold lower and tenfold broader than
the other, you will see that they don’t resemble each other at all.
They are radically different distributions. A milder version of this
is shown in figure 50.
If you do your work even moderately carefully, you will know your
uncertainties much more precisely than that. Furthermore, if you are
doing data analysis with anything resembling professionalism and due
diligence, you will need to know your uncertainties much more
precisely than that. One reason is that you will be using
weighted averaging and weighted curve fitting – weighted
inversely according to the variance – and accurate weighting is
important. This leads us yet again to a simple conclusion: Don’t use
significant figures. Instead, follow the guidelines in
section 8.2.
Returning now to even larger issues: Given something that is properly
expressed in the form A±B, sig figs do a lousy job of
representing the nominal value A ... not just the uncertainty B.
This is important!
|
Sig figs degrade both the nominal value and the uncertainty.
|
|
|
|
To say the same thing another way: The sig figs rules forbid people to
use enough guard digits. They require too much rounding. They
require excessive roundoff error.
This is a big deal, because all too often, the “sig-figs rules” are
taught as if they were mandatory, to the exclusion of any reasonable
way of doing business. It is really quite astonishing what some
authors say about the “importance” of sig figs.
In addition to the immediate, practical, quantitative damage that sig
figs do to the values of A and B, sig figs also lead to multiple
conceptual problems, as mentioned in section 1.3.
17.5 Excessively Rough Uncertainty
The “significant digits rules” cannot represent
the uncertainty more accurately than the nearest power of ten. For
example, they represent the distribution 45±3 in exactly the
same way as the distribution 45±1, but as we can see in
figure 50, these are markedly different distributions.
In the figure, the heavy black curve represents 45±1 while the
thin green curve represents 45±3. These curves certainly look
different. In this example the uncertainties differ by a factor of
three; if the difference had been closer to a factor of ten the
contrast would have been even more extreme.
17.5.1 Sectarian Differences
Within the sig-digs cult, there are sects that hold
mutually-incompatible beliefs. There is no consensus. You cannot get
a group of teachers to agree within an order of magnitude what
“significant figures” mean.
- The multi-count sect says that you should write
down all the certain digits, plus one estimated digit.
That makes a certain amount of sense when you are recording readings
from laboratory apparatus and instruments. The point is that you want
the quantization error (i.e. roundoff error) to be smaller than the
the intrinsic uncertainty of the instrument. You want the uncertainty
of the recorded reading to be dominated by the intrinsic uncertainty
of the instrument, and not needlessly increased by rounding.
As is always the case with any form of significant digits, we run into
trouble because of the coarseness of the encoding; it is impossible
to know by looking at the number how much uncertainty there is
in the last digit.
Things get even worse when we consider calculated (rather than
observed) numbers. For example, consider the distribution 5.123(9).
Nine counts of uncertainty in the third decimal place not only makes
the third place uncertain, it makes the second place “somewhat”
uncertain. There is no logical basis for deciding how much
uncertainty is “too much”, i.e. deciding when to drop a digit.
For present purposes, let’s assume that this sect puts the cutoff just
shy of ten counts, so that 1.234(9) will be expressed as 1.234, while
1.234(10) will be rounded to 1.23. (We ignore sub-sects that put the
cutoff elsewhere.)
This sect has the advantage, relatively speaking, of requiring less
rounding than the other sects mentioned below ... but in absolute
terms it still requires too much rounding. It can seriously
degrade your data, as discussed in section 7.12.
- The percent sect holds as follows:
-
A one-digit number has an uncertainly between 10%
and 100%.
- A two-digit number has an uncertain between 1%
and 10%.
- A three-digit number has an uncertain between 0.1%
and 1%.
- Et cetera.
- The half-count sect holds that there is only half a count
of uncertainty in the last digit.
This rule actually makes sense provided you know that the
quantity has been rounded off, and that roundoff error is the dominant
contribution to the uncertainty.
On the other hand, there are innumerable important situations where
roundoff should not the dominant contribution, in which case
this is the worst of all the sects. It causes the most data
destruction, because it demands the most rounding. It demands an
order of magnitude more rounding than the few-count sect. It
basically forces you to keep rounding off until the roundoff error
becomes a large contribution to the uncertainty.
Let’s try applying these “rules” and see what happens. Some
examples are shown in the following table.
| | | 0.10 | | 0.99 |
|
| multi-count sect: | | 0.100(10) ⋯ 0.100(99) | | 0.990(10) ⋯ 0.990(99) |
| percent sect: | | 0.100(1) ⋯ 0.100(10) | | 0.990(10) ⋯ 0.990(99) |
| half-count sect: | | 0.100(5) | | 0.990(5) |
| overall range: | | 0.100(1) ⋯ 0.100(99) | | 0.990(5) ⋯ 0.990(99) |
Let’s consider 0.10, as shown in the table. If we interpret 0.10
according to the multi-count sect’s rules, we get something in the
range 0.100(10) to 0.100(99). Meanwhile, if we interpret that
according to the percent-sect’s rules, we get something in the range
0.100(1) to 0.100(10). Ouch! These two sects don’t even overlap;
that is, they don’t have any interpretations in common, except on a
set of measure zero. Last but not least, the half-count sect
interprets 0.10 as 0.100(5), which is near the middle of the range
favored by the percent-sect ... and far outside the range favored by
the multi-count sect.
Next, let’s consider 0.99. If we interpret 0.99 according to the
multi-count sect’s rules, we get something in the range 0.990(10) to
0.990(99). Meanwhile, if we interpret it according to the percent
sect’s rules and convert to professional notation, we get something in
the range 0.990(10) to 0.990(99). So these two sects agree on the
interpretation of this number. However, the half-count sect
interprets 0.99 as 0.990(5), which is somewhere between 2x and 20x
less uncertainty than the other sects would have you believe.
As shown in the bottom row of the table, when we take sectarian
differences into account, there can be two orders of magnitude
of vagueness as to what a particular number represents. If you draw
the graph of two distributions, one of which is a hundredfold lower
and a hundredfold broader than the other, the difference is shocking.
It’s outrageous. You cannot possibly consider one to be a useful
approximation to the other.
17.5.2 Exact Numbers Are Not Describable Using Sig Figs
Consider the notion that one inch equals some number of centimeters.
If you adhere to the sig-figs cult, how many digits should you use to
express this number? It turns out that the number is 2.54, exactly,
by definition. Unless you want to write down an infinite number of
digits, you are going to have to give up on the idea of sig figs
and express the uncertainty separately, as discussed in
section 8.2.
Suppose you see the number 2.54 in the display of a calculator. How
much significance attaches to that number? You don’t know! Counting
digits will not tell you anything about the uncertainty.
Calculators are notorious for displaying large numbers of
insignificant digits, so counting digits might cause you to seriously
underestimate the uncertainty (i.e. overestimate the precision). On
the other hand, 2.54 might represent the centimeter-per-inch
conversion factor, in which case it is exact, and counting digits will
cause you to spectacularly overestimate the uncertainty
(i.e. underestimate the precision).
17.5.3 Null Experiments Are Not Describable Using Sig Figs
A number such as 4.32±.43 expresses an absolute uncertainty of
.43 units. A number such as 4.32±10% expresses a relative
uncertainty of 10%. Both of these expressions describe nearly the
same distribution, since 10% of 4.32 is nearly .43.
Sometimes relative uncertainty is convenient for expressing the
idea behind a distribution, sometimes absolute uncertainty is
convenient, and sometimes you can do it either way.
It is interesting to consider the category of null experiments,
that is, experiments where the value zero lies well within the
distribution that describes the results. Null experiments are fairly
common, and some of them are celebrated as milestones or even
turning-points in the history of science. Examples include the
difference between gravitational and inertial mass (Galileo,
Eötvös, etc.), the luminiferous ether (Michelson and Morley), the
mass of the photon, the rate-of-change of the fine-structure constant
and other fundamental “constants” over time, et cetera.
The point of a null experiment is to obtain a very small
absolute uncertainty.
Suppose you re-do the experiment, improving your technique by a factor
of ten, so that the absolute uncertainty σA of the result goes
down by a factor of ten. You can expect that the mean value of the
result mA will also go down by a factor of ten, roughly. So to a
rough approximation the relative uncertainty is unchanged, even though
you did a much better experiment.
On closer scrutiny we see that the idea of relative uncertainty never
did make much sense for null experiments. For one thing, there is
always the risk that the mean value mA might come out to be zero.
(In a counting experiment, you might get exactly zero counts.)
In that case, the relative uncertainty is infinite, and certainly
doesn’t tell you anything you need to know.
Scientists have a simple and common-sensical solution: In such cases
they quote the absolute uncertainty, not the relative uncertainty.
Life is not so simple if you adhere to the sig-figs cult. The problem
is that the sig-figs rules always express relative uncertainty.
To put an even finer point on it, consider the case where the relative
uncertainty is greater than 100%, which is what you would expect for
a successful null experiment. For concreteness, consider
.012±.034. How many digits should be used to express such a result?
Let’s consider the choices:
-
Zero digits is too few. It doesn’t tell us enough about the
mean value mA.
- One digit is too many, if you follow the sig-figs rules, because
they understate the uncertainty σA by a huge factor.
Exaggerating the precision and/or accuracy of your results will ruin
your scientific reputation.
- More than one digit is far too many, for the same reason.
Bottom line: There is an important class of distributions that simply
cannot be described using the significant-figures method. This
includes distributions that straddle the origin. Such distributions
are common; indeed they are expected in the case of null experiments.
17.5.4 Some Other Inexact Numbers Are Not Describable Using Sig Figs
In addition to distributions that straddle the origin (as discussed in
section 17.5.3), there are some that do not straddle the origin
but are nevertheless so broad that they cannot be well described using
significant digits.
Let’s look again at the example of the six-sided die, as depicted in
figure 12. The number of spots can be described by the expression
x=3.5±2.5. There is just no good way to express this using
significant figures. If you write x=3.5, those who believe in sig
figs will interpret that as perhaps x=3.5[½] or x=3.5(5) or
somewhere in between … all of which greatly understate the
width of the distribution. If you round off to x=3, that would
significantly misstate the center of the distribution.
As a second example, let’s look again at the result calculated in
section 7.21, namely 2.4(8). Trying to express this
using sig digs would be a nightmare. If you write it as
2.4 and let the reader try to infer how much uncertainty there is,
the most basic notions of consistency would suggest that this number
has about the same amount of uncertainty as the two-digit number in
the statement of the problem ... but in fact it has a great deal more,
by a ratio of about eight to three. That is, any consistently-applied
sig-digs rule understates the uncertainty of this expression.
The right answer is about 260% of the “sig-figs answer”.
Note that the result 2.4(8) has eight counts of uncertainty in the
last digit. Another way of saying the same thing is that there is
32% relative uncertainty. That’s so much uncertainty that if you
adhere to the percent-sect (as defined in section 17.5.1) you are
obliged to use only one significant digit. That means means converting
2.4 to 2. That result differs from the correct value by 57% of an
error bar, which is a significant degradation of your hard-won data,
in the sense that the distribution specified by 2.45(79) is just not
the same as a distribution centered on 2, no matter what width you
attach to the latter.
So we discover yet again that the “sig-digs” approach gives us no
reasonable way of expressing what needs to be expressed.
Consider the following contrast:
|
Suppose some distribution has a nominal value of A and an
uncertainty of B. We can write this as A±B, even when we do
not yet know the values of A and/or B. We can then find these A
and B using algebra.
|
|
There is no way to express
A±B using significant figures, when A and/or B are
abstract or not yet known.
|
|
The same idea applies to electronic computations, including
hand calculators, spreadsheets, c++ programs, et cetera. You can use
a variable A and a variable B to represent the distribution
A±B.
|
|
I have never seen a computer represent uncertainty
using significant figures.
|
To approach the same idea from a different direction:
|
Often it is important to think about numbers as numbers,
without reference to any particular system of numerals.
|
|
The notion
of significant figures, to the extent that it means anything at all,
applies to decimal numerals, not to numbers per se.
|
Therefore (unless you are going to forfeit the possibility of doing
any algebra or any electronic computation) you need to learn the
“±” concept and terminology.
Once you have learned this, you might as well use it for everything,
to the exclusion of anything resembling significant figures.
17.5.6 Units Won’t Solve the Problem
Suppose somebody asks you what is 4 times 2.1. If you adhere to the
sig-figs cult, you can’t tell from the statement of the problem
whether the numeral 4 is trying to represent a probability
distribution (centered at 4 with one sig-fig of uncertainty), or
whether it is meant to be an exact quantity (plain old
4).
-
In one scenario, you write down the number 2.1 four times,
and add them all up. The four is exact.
- In another scenario, your assistant has measured the aspect
ratio of a piece of paper, and found it to be approximately 4.
This is a measured quantity. You may believe on theoretical grounds
that this observation was drawn from a distribution, and that the
distribution has some uncertainty, but alas we don’t have a good
estimate of the uncertainty because the assistant foolishly tried to
express it using the sig-figs method.
Occasionally somebody tries to distinguish these two cases by making a
fuss about units. The idea apparently is that all inexact quantities
are measured and have units, and conversely all quantities with units
are measured and therefore inexact. Well, this idea is false. Both
the obverse and converse are false.
For example:
-
The aspect ratio mentioned above is measured and inexact,
but dimensionless.
- Conversely, in the SI system, the speed of light
is exact but has dimensions. (Specifically, the value is
2.99792458×108±0 m/s by definition. See
e.g. reference 36.)
To summarize: Dimensionless does not imply exact. Exact does not
imply dimensionless. Trying to estimate uncertainty by counting the
digits in a numeral is a guaranteed losing proposition, and making a
fuss about units does not appreciably alleviate the problem.
17.5.7 Decimals Are Exact By Definition
There is no mathematical principle that associates any uncertainty
with a decimal numeral such as 2.54. On the contrary, 2.54 is
defined to be a rational number, i.e. the ratio of two integers,
in this case 254/100 or in lowest terms 127/50. In such
ratios, the numerator is an exact integer, the denominator is an exact
integer, and therefore the ratio is an exact rational number.
By way of contrast, sometimes it may be convenient to approximate a
rational number; for instance the ratio 173/68 may be
rounded off to 2.54[⁄] if you think the roundoff error
is unimportant in a given situation. Still, the point remains that
2.54[⁄] is not the same thing as 2.54.
17.5.8 Ambiguity Is Not an Advantage
Once I was discussing a distribution that had been calculated to be
x=2.1(2). A sig-figs partisan objected that sometimes you don’t
know that the uncertainty is exactly 0.2 units, and in such a case it
was preferable to write x=2.1 using sig figs, thereby making a vague
and ambiguous statement about the uncertainty. The fact that nobody
knows what the sig figs expression really means was claimed to be an
advantage in such a case. Maybe it means x=2.1[½], or maybe
x=2.1(5), or maybe something else.
There are several ways of seeing how silly this claim is. First of
all, even if the claim were technically true, it would not be worth
learning the sig-figs rules just to handle this unusual case.
Secondly, nobody ever said the uncertainty was “exactly” 0.2 units. In
the expression x=2.1(2), nobody would interpret the (2) as being
exact, unless they already belonged to the sig-fig cult. The rest of
us know that the (2) is just an estimate.
Thirdly, it is true that the notation x=2.1(2) or equivalently
x=2.1±0.2 does not solve all the world’s problems. However, if
that notation is problematic, the solution is not to switch to a
worse notation such as sig figs. Instead, you should switch to
a better notation, such as plain language. If you don’t have a good
handle on the uncertainty, just say so. For example, you could say
“we find x=2.1. The uncertainty has not been quantitatively
analyzed, but is believed to be on the order of 10%”. This adheres
to the wise, simple rule:
Say what you mean,
and mean what you say.
|
|
|
|
Sig figs neither say what they mean nor mean what they say.
18 Appendix: Place Value and Mantissa Digits
There exists a purely mathematical concept of “place value” which is
related to the concept of significance. We mention it only for
completeness, because it is never what chemistry textbooks mean when
they talk about “significant digits”.
For example, in the numeral 12.345, the “1” is has the highest place
value, while the “5” has the lowest place value.
Sometimes the term “significance” is used to express this
mathematical idea. For example, in the numeral 12.345, the “1” is
called the most-significant digit, while the “5” is called the
least-significant digit. These are relative terms, indicating that
the “1” has relatively more significance, while the “5” has
relatively less significance. We have no way of knowing whether any
of the digits has any absolute significance with respect to any real
application.
This usage is common, logical, and harmless. However, since the other
usages of the term “significant digit” are so very harmful, it may
be prudent to avoid this usage as well, especially since some
attractive alternatives are available. One option is to speak of
place value (rather than significance) if that’s what you mean.
Another option is to speak of mantissa digits. For example, if
we compare 2.54 with 2.5400, the trailing zeros have no effect on the
mantissa. (In fact, they don’t contribute to the characteristic,
either, so they are entirely superfluous, but that’s not relevant to
the present discussion.) Similarly, if we compare 2.54 to 002.54, the
leading zeros don’t contribute to the mantissa (or the
characteristic).
It is more interesting to compare .0254 with .000254. In this case,
the zeros do not contribute to the mantissa (although they do
contribute to the characteristic, so they are not superfluous). This
is easy to see if we rewrite the numbers in scientific notation,
comparing 2.54×10−2 versus 2.54×10−4.
To make a long story short, the mantissa digits are all the digits
from the leftmost nonzero digit to the rightmost nonzero digit,
inclusive. For example, the number 0.00008009000 has four mantissa
digits, from the 8 to the 9 inclusive. In more detail, we say it has
a superfluous leading zero, then four place-holder digits, then
four mantissa digits, then four superfluous trailing zeros.
Keep in mind that the number of mantissa digits does not tell you
anything about the uncertainty, accuracy, precision, readability,
reproducibility, tolerance, or anything like that. If you see a
number with N digits of mantissa, it does not imply or even suggest
that the number was rounded to N digits; it could well be an exact
number, as in 2.54 centimeters per inch or 2.99792458×108
meters per second.
When the number system is taught in elementary school, mantissa digits
are called “significant digits”. This causes conflict and
confusion when the high-school chemistry text uses the same term with
a different meaning. For example, some people would say that 0.025400
has three significant digits, while others would say it has five
significant digits. I don’t feel like arguing over which meaning is
“right”. Suggestions:
-
It is OK to say that 0.025400 has three mantissa digits.
- If x has 10 ppm of uncertainty, express it by saying “10
ppm”. For example, x = 0.025400 ± 10 ppm or
equivalently x = 0.0254 ± 10 ppm.
- Avoid anything involving significant digits. If x has 10 ppm
of uncertainty, as in the previous example, do not attempt to express
it in terms of 5 sig figs or any other number of sig figs.
19 Appendix: Resistor Values
This section continues the discussion that began in
section 5.5. It makes the point that the relationship
between indicated value and true value does not need to be simple or
evenly spaced.
Suppose you wanted to measure some 5% resistors and sort them into
bins. The industry-standard bin-labels are given in the following
table, along with the corresponding intervals:
| indicated | | range of |
| value | | true values |
| 1.0 | : | [0.95, | 1.05] |
| 1.1 | : | [1.05, | 1.15] |
| 1.2 | : | [1.15, | 1.25] |
| 1.3 | : | [1.25, | 1.4] |
| 1.5 | : | [1.4, | 1.55] |
| 1.6 | : | [1.55, | 1.7] |
| 1.8 | : | [1.7, | 1.9] |
| 2.0 | : | [1.9, | 2.1] |
| 2.2 | : | [2.1, | 2.3] |
| 2.4 | : | [2.3, | 2.55] |
| 2.7 | : | [2.55, | 2.85] |
| 3.0 | : | [2.85, | 3.15] |
| 3.3 | : | [3.15, | 3.45] |
| 3.6 | : | [3.45, | 3.75] |
| 3.9 | : | [3.75, | 4.1] |
| 4.3 | : | [4.1, | 4.5] |
| 4.7 | : | [4.5, | 4.9] |
| 5.1 | : | [4.9, | 5.34] |
| 5.6 | : | [5.34, | 5.89] |
| 6.2 | : | [5.89, | 6.49] |
| 6.8 | : | [6.49, | 7.14] |
| 7.5 | : | [7.14, | 7.79] |
| 8.1 | : | [7.79, | 8.59] |
| 9.1 | : | [8.59, | 9.54] |
| 10. | : | [9.54, | 10.49] |
It may not be obvious at first, but this table does have a somewhat
logical basis. Roughly speaking, it comes from rounding the readings
to the nearest 1/24th of 20dB, exponentiating, and then rounding to
one decimal place. For what it’s worth, note that even in the absence
of roundoff, it would be barely possible to cover the entire decade
and still keep all the readings within 5% of the nominal bin label.
That’s because 1.05 is too small and/or 24 is too few. Roundoff makes
it impossible. One consequence is that if you want a resistance of
1.393 kΩ, you cannot approximate it within 5% using any
standard 5% resistor. You can’t even approximate it within 7%.
20 References
-
-
Clifford E. Swartz,
“Insignificant figures”
Phys. Teach. 6, 125 (March 1968).
http://tpt.aapt.org/resource/1/phteah/v6/i3/p125_s1 -
John Denker,
“Introduction to Probability”
www.av8n.com/physics/probability-intro.htm -
H. Bradford Thompson,
“Is 8∘C equal to 50∘F?
J. Chem. Educ. 68 (5), p 400 (1991).
http://pubs.acs.org/doi/pdf/10.1021/ed068p400
~~~
Also known as: “Good Enough for Chemistry (a tragedy in three scenes)”
http://web.archive.org/web/20020805023358/http://prob.org/readings/sigdig/ -
John Denker,
“Tack Tossing : An Exercise in Probability”
www.av8n.com/physics/tack-tossing.htm -
John Denker,
“Spreadsheet to create band plots”
www.av8n.com/physics/uncertainty-distro-not-points.xls
-
John R. Taylor
An Introduction to Error Analysis:
The Study of Uncertainties in Physical MeasurementsThis is sometimes called “the train book” because
of the cover, which features a
crashed train at the Gare Montparnasse, 22 October 1895.
It’s a beautiful photograph, but alas it conveys
completely the wrong idea about what we mean by “error”
in the context of error analysis, as discussed
in section~5.6.
In the first 70 pages, the book contains many formulas, none of
which can safely be applied to real data, as far as I can tell.
-
NIST
“Fundamental Physical Constants : elementary charge”
http://physics.nist.gov/cgi-bin/cuu/Value?e -
NIST
“Essentials of expressing measurement uncertainty”
http://physics.nist.gov/cuu/Uncertainty/basic.html -
NIST
“International and U.S. perspectives on measurement uncertainty”
http://physics.nist.gov/cuu/Uncertainty/international1.html -
NIST Technical Note 1297
“Guidelines for Evaluating and Expressing
the Uncertainty of NIST Measurement Results”
http://physics.nist.gov/Pubs/guidelines/TN1297/tn1297s.pdf -
BIPM / Joint Committee for Guides in Metrology
“GUM: Guide to the Expression of Uncertainty in Measurement”
Index: http://www.bipm.org/en/publications/guides/gum.html
current version: http://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf -
Pekka K. Sinervo
“Definition and Treatment of Systematic Uncertainties in High Energy
Physics and Astrophysics”
http://www.slac.stanford.edu/econf/C030908/papers/TUAT004.pdf -
John Denker,
“pH versus Concentration”
www.av8n.com/physics/ph-versus-concentration.htm -
John Denker,
“Quadratic Formula : Numerically Well-Behaved Version”
www.av8n.com/physics/quadratic-formula.htm -
Forman S. Acton,
Numerical Methods that Work
Mathematical Association of America (1st edition 1970)
(updated and reissued 1990)
-
John Denker,
Spreadsheet for extracting a signal
from noisy data, with and without bogus roundoff
www.av8n.com/physics/roundoff.xls
-
Zumdahl, Chemistry (5th edition).
-
John Denker,
“Introduction to Atoms”
www.av8n.com/physics/atom-intro.htm -
International Union of Pure and Applied Chemistry,
“ISOTOPIC COMPOSITIONS OF THE ELEMENTS” (1997)
http://www.iupac.org/reports/1998/7001rosman/iso.pdf -
International Union of Pure and Applied Chemistry,
“Atomic Weights of the Elements” (2000)
http://www.iupac.org/publications/pac/2003/pdf/7506x0683.pdf -
E. J. Catanzaro, T. J. Murphy, E. L. Garner, and W. R. Shields,
“Absolute Isotopic Abundance Ratios and Atomic Weight of Magnesium”
J. Res. NBS (1966).
http://nvlpubs.nist.gov/nistpubs/jres/070/6/V70.N06.A01.pdf -
Magnesium Mass Monte Carlo:
www.av8n.com/physics/mg-digs.html
and the spreadsheet used to calculate it:
www.av8n.com/physics/mg-digs.xls
-
John Denker,
“Spreadsheet Tips and Techniques”
www.av8n.com/physics/spreadsheet-tips.htm -
John Denker,
“spreadsheet for calculating pH”
./ph-scan.xls
-
John Denker,
“Nonlinear Least Squares”
www.av8n.com/physics/nonlinear-least-squares.htm -
John Denker, “Scientific Methods”
www.av8n.com/physics/scientific-methods.htm -
Michael Edmiston, “advice for acquiring and
recording lab data”,
http://www.bluffton.edu/~edmistonm/acquiring.recording.data.pdf -
IAU Division I Working Group
“Numerical Standards for Fundamental Astronomy
Astronomical Constants : Current Best Estimates (CBEs)”
http://maia.usno.navy.mil/NSFA/NSFA_cbe.html -
“The NIST Reference on Constants, Units, and Uncertainty”
http://physics.nist.gov/cgi-bin/cuu/Value?bg -
John William Strutt, Lord Rayleigh, “Argon”
Royal
Institution Proceedings 14, 524 (1895).
http://web.lemoyne.edu/~giunta/Rayleigh.html -
Eric W. Weisstein, “Standard Deviation” entry at Mathworld
http://mathworld.wolfram.com/StandardDeviation.html -
Eric W. Weisstein, “Standard Error” entry at Mathworld
http://mathworld.wolfram.com/StandardDeviation.html -
BIPM / Joint Committee for Guides in Metrology
“VIM3: International Vocabulary of Metrology”
Index: http://www.bipm.org/en/publications/guides/vim.html
current version: http://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2012.pdf -
Edoardo Milotti, “1/f noise: a pedagogical review”
http://arxiv.org/pdf/physics/0204033.pdf -
Lowell M. Schwartz,
“Propagation of significant figures,”
J. Chem. Educ. 62, 693 (1985).
http://pubs.acs.org/doi/abs/10.1021/ed062p693
-
The official SI value of the speed of light,
http://physics.nist.gov/cgi-bin/cuu/Value?c
Footnotes