Figure 1.2: Two Potatoes + Heat Engine
Some things in this world are so fundamental that they cannot be defined in terms of anything more fundamental. Examples include:
| Do not place too much emphasis on pithy, dictionary-style definitions. You need to have a vocabulary of many hundreds of words before you can even begin to read the dictionary. | The general rule is that words acquire meaning from how they are used. For many things, especially including fundamental things, this is the only worthwhile definition you are going to get. |
| The dictionary approach often leads to circularity. For example, it does no good to define energy in terms of work, define work in terms of force, and then define force in terms of energy. | The real definition comes from how the word is used. The dictionary definition is at best secondary, at best an approximation to the real definition. |
Geometry books often say explicitly that points, lines, and planes are “undefined” terms, but I prefer to say that they are implicitly defined. Equivalently, one could say that they are retroactively defined, in the sense that they are used before they are defined. They are initially undefined, but then gradually come to be defined. They are defined by how they are used in the axioms and theorems.
Here is a quote from page 71 of reference 5:
Here and elsewhere in science, as stressed not least by Henri Poincare, that view is out of date which used to say, “Define your terms before you proceed.” All the laws and theories of physics, including the Lorentz force law, have this deep and subtle character, that they both define the concepts they use (here B and E) and make statements about these concepts. Contrariwise, the absence of some body of theory, law, and principle deprives one of the means properly to define or even to use concepts. Any forward step in human knowledge is truly creative in this sense: that theory, concept, law, and method of measurement — forever inseparable — are born into the world in union.
In other words, it is more important to understand what energy does than to rote-memorize some dictionary-style definition of what energy «is».
We can apply this idea as follows:
The most salient thing that energy does is to uphold the local energy-conservation law, equation 1.1.
That means that if we can identify one or more forms of energy, we can identify all the others by seeing how they plug into the energy-conservation law. A catalog of possible starting points and consistency checks is given in equation 1.2 in section 1.3.
The first law of thermodynamics states that energy obeys a local conservation law.
By this we mean something very specific:
Any decrease in the amount of energy in a given region of space must be exactly balanced by a simultaneous increase in the amount of energy in an adjacent region of space.
Note the adjectives “simultaneous” and “adjacent”. The laws of physics do not permit energy to disappear now and reappear later. Similarly the laws do not permit energy to disappear from here and reappear at some distant place. Energy is conserved right here, right now.
It is usually possible1 to observe and measure the physical processes whereby energy is transported from one region to the next. This allows us to express the energy-conservation law as an equation:
| (1.1) |
The word “flow” in this expression has a very precise technical meaning, closely corresponding to one of the meanings it has in everyday life. See reference 6 for the details on this.
There is also a global law of conservation of energy: The total energy in the universe cannot change. The local law implies the global law but not conversely. The global law is interesting, but not nearly as useful as the local law, for the following reason: suppose I were to observe that some energy has vanished from my laboratory. It would do me no good to have a global law that asserts that a corresponding amount of energy has appeared “somewhere” else in the universe. There is no way of checking that assertion, so I would not know and not care whether energy was being globally conserved.2 Also it would be very hard to reconcile a non-local law with the requirements of special relativity.
As discussed in reference 6, there is an important distinction between the notion of conservation and the notion of constancy. Local conservation of energy says that the energy in a region is constant except insofar as energy flows across the boundary.
Consider the contrast:
| The conservation law presented in section 1.2 does not, by itself, define energy. That’s because there are lots of things that obey the same kind of conservation law. Energy is conserved, momentum is conserved, electric charge is conserved, et cetera. | On the other hand, examples of energy would not, by themselves, define energy. |
| On the third hand, given the conservation law plus one or more examples of energy, we can achieve a pretty good understanding of energy by a two-step process, as follows: |
For reasons explained in section 1.1, we introduce the terms energy, momentum, and mass as initially-undefined terms. They will gradually acquire meaning from how they are used.
Here are a few well-understood examples of energy. Please don’t be alarmed by the length of the list. You don’t need to understand every item here; indeed if you understand any one item, you can use that as your starting point for the two-step process mentioned above.
|
In particular, if you need a starting-point for your understanding of energy, perhaps the simplest choice is kinetic energy. A fast-moving book has more energy than it would at a lower speed. Some of the examples in equation 1.2 are less fundamental than others. For example, it does no good to define energy via equation 1.2j, if your definition of voltage assumed some prior knowledge of what energy is. Also, equation 1.2c, equation 1.2d and equation 1.2e can all be considered corollaries of equation 1.2b. Still, plenty of the examples are fundamental enough to serve as a starting point. For example:
The examples that you don’t choose as the starting point serve as valuable cross-checks.
We consider things like Planck’s constant, Coulomb’s constant, and the speed of light to be already known, which makes sense, since they are universal constants. We can use such things freely in our effort to understand how energy behaves.
It must be emphasized that we are talking about the physics energy. Do not confuse it with plebeian notions of “available energy” as discussed in section 1.7 and especially section 1.8.1.
The description of energy in section 1.3 is recursive. That means we can pull our understanding of energy up by the bootstraps. We can identify new forms of energy as they come along, because they contribute to the conservation law in the same way as the already-known examples. This is the same basic idea as in reference 8.
Recursive is not the same as circular. A circular argument would be fallacious and useless ... but there are many examples of correct, well-accepted definitions that are recursive. Note one important distinction: Circles never end, whereas a properly-constructed recursion does end.3 Recursion is very commonly used in mathematics and computer science. For example, it is correct and convenient to define the factorial function so that
| (1.3) |
As a more sophisticated example, have you ever wondered how mathematicians define the concept of integers? One very common approach is to define the positive integers via the Peano axioms. The details aren’t important, but the interesting point is that these axioms provide a recursive definition … not circular, just recursive. This is a precise, rigorous, formal definition.
This allows us to make another point: There are a lot of people who are able to count, even though they are not able to provide a concise definition of “integer” – and certainly not able to provide a non-recursive definition. By the same token, there are lots of people who have a rock-solid understanding of how energy behaves, even though they are not able to give a concise and/or non-recursive definition of “energy”.
Energy is an abstraction. This is helpful. It makes things very much simpler. For example, suppose an electron meets a positron. The two of them annihilate each other, and a couple of gamma rays go flying off, with 511 keV of energy apiece. In this situation the number of electrons is not conserved, the number of positrons is not conserved, the number of photons is not conserved, and mass is not conserved. However, energy is conserved. Even though energy cannot exist without being embodied in some sort of field or particle, the point remains that it exists at a different level of abstraction, separate from the field or particle. We can recognize the energy as being the same energy, even after it has been transferred from one particle to another. This is discussed in more detail in reference 9.
Energy is completely abstract. You need to come to terms with this idea, by accumulating experience, by seeing how energy behaves in various situations. As abstractions go, energy is one of the easiest to understand, because it is so precise and well-behaved.
As another example, consider figure 1.1. (Video courtesy of GiantNewtonsCradle.com.) Initially there is some energy in ball #1. The energy then flows through ball #2, ball #3, and ball #4 without accumulating there. It accumulates in ball #5, which goes flying.
The net effect is that energy has flowed out of ball #1 and flowed into ball #5. Even though the energy is embodied in a completely different ball, we recognize it as the same energy.
| The symbol E denotes “the” energy of the system we are considering. If you feel obliged to attach some sort of additional words, you can call E the “system” energy or the “plain old” energy. This doesn’t change the meaning. | Most other qualifiers change the meaning. There is an important conceptual point here: “The” energy is conserved, but (with rare exceptions) the various sub-categories of energy are not separately conserved. For example, the “available” energy is not necessarily conserved, as discussed in section 1.7. |
Associated with the foregoing general conceptual point, here is a specific point of terminology: E is the plain old total energy, not restricted to “internal” energy or “available” energy.
Non-experts sometimes try to relate energy to “the capacity to do work”. This is never a good idea, for several reasons, as we now discuss.
Consider the following example: We use an ideal battery connected to an ideal motor to raise a weight, doing work against the gravitational field. This is reversible, because we can also operate the motor in reverse, using it as a generator to recharge the battery as we lower the weight.
To analyze such a situation, we don’t need to know anything about thermodynamics. Old-fashioned elementary non-thermal mechanics suffices.
If you do happen to know something about thermodynamics, you can quantify this by saying that the temperature T is low, and the entropy S is small, such that any terms involving TΔS are negligible compared to the energy involved.On the other hand, if you don’t yet know TΔS means, don’t worry about it.
In simple situations such as this, we can define work as ΔE. That means energy is related to the ability to do work ... in this simple situation.
Even in situations where energy is related to the ability to do work, it is not wise to “define” energy that way, for a number of practical and pedagogical reasons.
Energy is so fundamental that it is not definable in terms of anything more fundamental. You can’t define energy in terms of work unless you already have a solid definition of “work”, and defining work is not particularly easier than defining energy from scratch. It is usually better to start with energy and define work in terms of energy (rather than vice versa), because energy is the more fundamental concept.
In general, some of the energy of a particular system is available for doing work, and some of it isn’t. The second law of thermodynamics, as discussed in chapter 2, makes it impossible to use all the energy (except in certain very special cases, as discussed in section 1.7.1).
See section 15.6 for more about this.
In this document, the word “energy” refers to the physics energy. However, when business executives and politicians talk about energy, they are generally more concerned about “available energy”, which is an important thing, but it is emphatically not the same as the physics energy. See section 1.8.1 for more about this. It would be a terrible mistake to confuse “available energy” with the physics energy. Alas, this mistake is very common. See section 15.6 for additional discussion of this point.
Any attempt to define energy in terms of “capacity to do work” would be inconsistent with thermodynamics, as we see from the following examples:
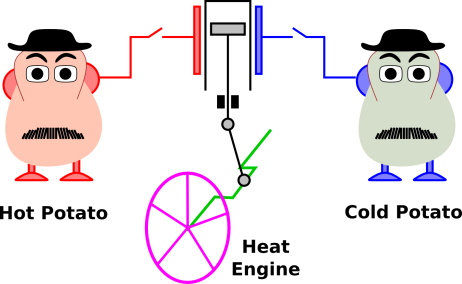
| #1: Consider an isolated system containing a hot potato, a cold potato, a tiny heat engine, and nothing else, as illustrated in figure 1.2. This system has some energy and some ability to do work. | #2: Contrast that with a system that is just the same, except that it has two hot potatoes (and no cold potato). |
The second system has more energy but less ability to do work.
This sheds an interesting side-light on the energy-conservation law. As with most laws of physics, this law, by itself, does not tell you what will happen; it only tells you what cannot happen: you cannot have any process that fails to conserve energy. To say the same thing another way: if something is prohibited by the energy-conservation law, the prohibition is absolute, whereas if something is permitted by the energy-conservation law, the permission is conditional, conditioned on compliance with all the other laws of physics. In particular, as discussed in section 9.2, if you want to transfer energy from the “collective” modes of a rapidly-spinning flywheel to the other modes, you have to comply with all the laws, not just conservation of energy. This includes conserving angular momentum. It also includes complying with the second law of thermodynamics.
Let’s be clear: The ability to do work implies energy, but the converse is not true. There are lots of situations where energy cannot be used to do work, because of the second law of thermodynamics or some other law.
Equating energy with doable work is just not correct. (In contrast, it might be OK to connect energy with some previously-done work, as opposed to doable work. That is not always convenient or helpful, but at least it doesn’t contradict the second law of thermodynamics.)
Some people wonder whether the example given above (the two-potato engine) is invalid because it involves closed systems, not interacting with the surrounding environment. Well, the example is perfectly valid, but to clarify the point we can consider another example (due to Logan McCarty):
| #1: Consider a system consisting of a room-temperature potato, a cold potato, and a tiny heat engine. This system has some energy and some ability to do work. | #2: Contrast that with a system that is just the same, but except that it has two room-temperature potatoes. |
The second system has more energy but less ability to do work in the ordinary room-temperature environment.
In some impractical theoretical sense, you might be able to define the energy of a system as the amount of work the system would be able to do if it were in contact with an unlimited heat-sink at low temperature (arbitrarily close to absolute zero). That’s quite impractical because no such heat-sink is available. If it were available, many of the basic ideas of thermodynamics would become irrelevant.
As yet another example, consider the system shown in figure 1.3. The boundary of the overall “system” is shown as a heavy black line. The system is thermally insulated from its surroundings. The system contains a battery (outlined with a red dashed line) a motor, and a switch. Internal to the battery is a small series resistance R1 and a large shunt resistance R2. The motor drives a thermally-insulated shaft, so that the system can do mechanical work on its surroundings.
| By closing the switch, we can get the system to perform work on its surroundings by means of the shaft. | On the other hand, if we just wait a moderately long time, the leakage resistor R2 will discharge the battery. This does not change the system’s energy (i.e. the energy within the boundary of the system) … but it greatly decreases the capacity to do work. |
This can be seen as analogous to the NMR τ2 process. An analogous mechanical system is discussed in section 11.5.5. All these examples share a common feature, namely a change in entropy with no change in energy.
To remove any vestige of ambiguity, imagine that the system was initially far below ambient temperature, so that the Joule heating in the resistor brings the system closer to ambient temperature. See reference 11 for Joule’s classic paper on electrical heating.
To repeat: In real-world situations, energy is not the same as “available energy” i.e. the capacity to do work.
What’s worse, any measure of “available” energy is not a function of state. Consider again the two-potato system shown in figure 1.2. Suppose you know the state of the left-side potato, including its energy E1, its temperature T1, its entropy S1, its mass m1, its volume V1, its free energy F1, and its free enthalpy G1. That all makes sense so far, because those are all functions of state, determined by the state of that potato by itself. Alas you don’t know what fraction of that potato’s energy should be considered thermodynamically “available” energy, and you can’t figure it out using only the properties of that potato. In order to figure it out, you would need to know the properties of the other potato as well.
|
Every beginner wishes for a state function that specifies the “available energy” content of a system. Alas, wishing does not make it so. No such state function can possibly exist.
(When we say two systems are “loosely in contact” we mean they are neither completely isolated nor completely in equilibrium.)
Also keep in mind that the law of conservation of energy applies to the real energy, not to the “available” energy.
Beware that the misdefinition of energy in terms of “ability to do work” is extremely common. This misdefinition is all the more pernicious because it works OK in simple non-thermodynamical situations, as discussed in section 1.7.1. Many people learn this misdefinition, and some of them have a hard time unlearning it.
In physics, there is only one meaning for the term energy. For all practical purposes, there is complete agreement among physicists as to what energy is. This stands in dramatic contrast to other terms – such as “heat” – that have a confusing multiplicity of technical meanings even within physics; see section 17.1 for more discussion of “heat”, and see chapter 20 for a more general discussion of ambiguous terminology.
The two main meanings of “energy” are different enough so that the difference is important, yet similar enough to be highly deceptive.
| The physics energy is conserved. It is conserved automatically, strictly, and locally, in accordance with equation 1.1. | In ordinary conversation, when people speak of “energy” – even in a somewhat-technical sense – they are usually talking about some kind of “available energy” or “useful energy” or something like that. This is an important concept, but it is very hard to quantify, and it is definitely not equal to the physics energy. Examples include the “Department of Energy” or the “energy industry”. |
For the next level of detail on this, see section 20.3.
In physics, there is almost5 only one definition of conservation. However, we run into trouble when we consider the plebeian meanings.
The two main meanings of “conservation” are different enough so that the difference is important, yet similar enough to be highly deceptive.
| The main physics definition of conservation is synonymous with continuity of flow, as defined in equation 1.1. See reference 6. | The plebeian notion of “conservation” means saving, preserving, not wasting, not dissipating. It definitely is not equivalent to continuity of flow. Example: “conservation” of endangered wildlife. |
For the next level of detail on this, see section 20.4.
Combining the two previous ideas, we see that the simple phrase “energy conservation” is practically begging to be misunderstood. You could suffer from two profound misconceptions in a simple two-word phrase.
A great many thermodynamics books emphasize the so-called «internal energy», denoted U or Ein. I have never found it necessary to make sense of this. Instead I reformulate everything in terms of the plain old energy E and proceed from there. For details, see section 7.7.
The law of conservation of energy has been tested and found 100% reliable for all practical purposes, and quite a broad range of impractical purposes besides.
Of course everything has limits. It is not necessary for you to have a very precise notion of the limits of validity of the law of conservation of energy; that is a topic of interest only to a small community of specialists. The purpose of this section is merely to indicate, in general terms, just how remote the limits are from everyday life.
If you aren’t interested in details, feel free to skip this section.
Here’s the situation: