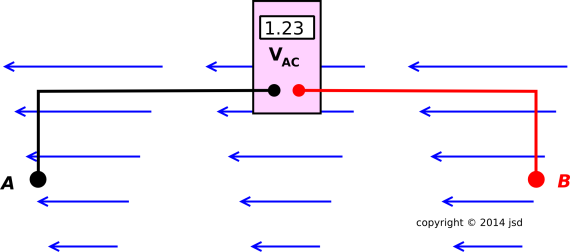
Figure 1: Definition of Voltage
The concept of voltage is derived from the concept of electromagnetic field. The voltage is not quite as fundamental, but is more convenient in a wide range of practical applications.
Voltage can be defined as the work done by a particle against the electric field, as the particle moves along a specified path from beginning to end. Specifically,
| (1) |
Here q is the charge on the particle, E is the electric field, Γ is the path, and ΔV is the change in voltage, as the particle moves along the path from beginning to end. The minus sign here corresponds to the minus sign in the principle of virtual work. The direction of increasing energy points up the hill, while the force points down the hill. V is energy per unit charge, while E is force per unit charge.
In connection with the work/KE theorem, equation 1 says that a charged particle loses kinetic energy as it runs into a region of higher qV (assuming no other forces are acting).
The situation is depicted in figure 1. The blue arrows indicate the direction and magnitude of the electric field. The path Γ is determined by the layout of the voltmeter leads, because that is the path that the charge must follow as it travels from point A to point B.
Note that voltage is defined with respect to a particular path. In figure 2, the voltage is substantially less than in the previous figure, even though the endpoints A and B are the same, and even though the electric field is everywhere the same. Different path, different voltage.
Now it turns out that in the low-frequency limit – for DC electric fields – the voltage is independent of the details of the path, so long as you keep the endpoints the same. This is a great convenience, as discussed in section 2. On the other hand, you shouldn’t get too enamored with it, because it does not apply to the general case, as discussed in section 3.
Voltage has dimensions of energy per unit charge. If we remove a factor of q from both sides of equation 1, we obtain a simpler and more elegant definition of voltage:
| (2) |
We have defined the change in voltage (ΔV), not the voltage itself. Therefore you are free to define a new voltage (V) that is equal to the old voltage plus a constant, and the laws of physics will treat the new voltage just the same. This property is called gauge invariance or gauge freedom. (You must however be consistent, using only the old voltage or only the new voltage. Mix&Match is not allowed.)
| (3) |
The constant G is called the gauge. When analyzing circuits, a common use of gauge freedom is to pick some point in the circuit and designate it to be zero voltage. The chosen zero-voltage point typically called the “ground reference” point, whether or not it bears any relationship to any nearby earth ground.
In this section, we restrict attention to the special case where the voltage does not depend on the details of the path Γ but only on the endpoints of the path. In such a case, we say that the voltage has the property of being a potential.
If the voltage is a potential, we can talk about “the” voltage at a point – not just Δ(voltage). We construct “the” voltage as follows. We choose a lot of different paths, all starting from some arbitrary reference point a, but with lots of different ending points b. Then for all b we have:
| (4) |
where Γ(a,b) is any path that goes from point a to point b. The location of point a is arbitrary but fixed. At this point, the voltage V(a) is arbitrary but fixed; it is an arbitrary reference voltage, aka gauge.
This construction gives us a well-defined voltage at each point, independent of how you got there. By “well-defined” we mean unique, except for the choice of gauge.
If the voltage is a potential, the electric field E is the gradient of the potential:
| (5) |
The voltage is provably a potential in the low frequency limit (i.e. the “DC” limit). We know this based on the Faraday law of induction, equation 6.
| (6) |
If the voltage is a potential then the term electrostatic potential is synonymous with voltage. If the voltage is not a potential, i.e. if the voltage is path-dependent, then the electrostatic potential does not exist. It would be a contradiction in terms. Remember, the voltage is still the voltage, whether or not the voltage is a potential.
Many important devices involve non-potential voltages. The voltages in figure 1 and figure 2 are non-potential voltages. Real-world examples include the internals of devices such as transformers, magnetos, generators (aka dynamos), and radios.
In everyday life, non-potential voltages are quite common. We are immersed in them. The voltage in a radio wave is 100% non-potential. The stray fields produced by motors, ballasts, and transformers have a large non-potential component. If you don’t believe me, do the experiment. The experiment can be done using an oscilloscope and a loop of wire. See reference 1.
If the voltage is not a potential, Kirchhoff’s Voltage “Law” is not valid. It might or might not be a good approximation. See reference 2.
Figure 3 may help you visualize what’s going on. It represents an electric field that is not the gradient of any potential. The diagram comes from reference 3. The reference explains how to interpret this kind of diagram, and contains lots more detail about non-potential voltages.
A volt is a unit of measurement, but a voltage is not. A voltage is the thing being measured. Don’t be fooled by the similarity in names. A titmouse is not a mouse. Buckwheat is not wheat. As Voltaire pointed out, the Holy Roman Empire was neither holy, nor Roman, nor an Empire. For more about weird and/or misleading terminology, see reference 4. For a general discussion of units of measurement, see reference 5.
As for the unit: When the word volt is spelled out, it is never italicized and never capitalized, in accordance with standard SI conventions. Similarly, when the word volt is abbreviated V, it is never italicized but always capitalized.
As for the thing being measured: The voltage is ordinarily represented by the variable V or v. In practical situations, there are usually many different voltages, so we put subscripts on the variables: Vi, Vo, v1, v2, et cetera. The subscript makes it easy to distinguish the thing being measured (Vo) from the unit of measurement (V).
Also note that the variable V is supposed to be italicized, which is another way that you can distinguish the voltage V from the unit of measurement V. On the other hand, sometimes italics are not available, e.g. in ASCII email. If you wanted to cause trouble, you could write 2 V = 3 V which is hopelessly ambiguous. Presumably one of those Vs is a variable, but we don’t know which one. So, as Henny Youngman would say: Don’t write things like that.
All in all, various ways to prevent ambiguity include:
EMF is not synonymous with voltage, because only a subset of the world’s voltages are given the name EMF. For example, in a linear circuit, the Thévenin equivalent open-circuit voltage is sometimes called the EMF, whereas the observed voltage at the terminals of the black box is not. My advice: There is never a good reason to use the term EMF, and the risk of being misunderstood is too great. If you mean open-circuit voltage, call it the open-circuit voltage. Why learn a new and a confusing term like EMF when you could use a straightforward term like open-circuit voltage instead?
The idea of Thévenin and Norton equivalent circuits is quite simple yet powerful. For an unnecessarily-complicated discussion, see reference 6 and reference 7.
The notion of electrical “tension” went out of fashion in the 1800s and the term is exceedingly rare nowadays in English. On the other hand, French still uses “tension”, Spanish uses “tensión”, and German uses “Spannung”. These words mean the same thing as tension (electrically, mechanically, and figuratively).
In an overhead wire, the mechanical tension runs along the wire from end to end, but the electrical tension does not. Instead it runs mostly perpendicular to the wire. It could be measured by observing the attraction between the wire and an oppositely-charged wire.