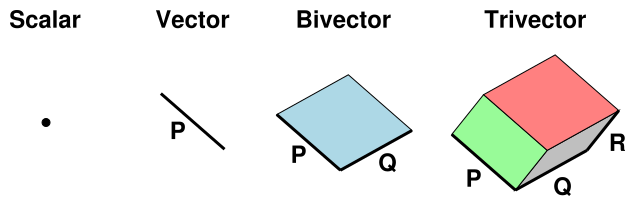
Figure 1: Scalar, Vector, Bivector, and Trivector
The purpose of this note is to provide a simple introduction to Clifford algebra, also known as geometric algebra. I assume that you have at least some prior exposure to the idea of vectors and scalars. (You do not need to know anything about matrices.)
For a discussion of why Clifford algebra is useful, see section 3.
This document is also available in PDF format. You may find this advantageous if your browser has trouble displaying standard HTML math symbols.
In addition to scalars and vectors, we will find it useful to consider more-general objects, including bivectors, trivectors, et cetera. Each of these objects has a clear geometric interpretation, as summarized in figure 1.
That is, a scalar can be visualized as an ideal point in space, which has no geometric extent. A vector can be visualized as line segment, which has length and orientation. A bivector can be visualized as a patch of flat surface, which has area and orientation. Continuing down this road, a trivector can be visualized as a piece of three-dimensional space, which has a volume and an orientation.
Each such object has a grade, according to how many dimensions are involved in its geometric extent. Therefore we say Clifford algebra is a graded algebra. The situation is summarized in the following table.
| object | visualized as | geometric extent | grade | |||
| scalar | point | no geometric extent | 0 | |||
| vector | line segment | extent in 1 direction | 1 | |||
| bivector | patch of surface | extent in 2 directions | 2 | |||
| trivector | piece of space | extent in 3 directions | 3 | |||
| etc. | ||||||
For any vector V you can visualize 2V as being twice as much length, and for any bivector B you can visualize 2B as having twice as much area. Alas this system of geometric visualization breaks down for scalars; geometrically all scalars “look” equally pointlike. Perhaps for a scalar s you can visualize 2s as being twice as hot, or something like that.
For another important visualization idea, see section 1.12.
We shall see in section 3 that bivectors make cross products obsolete; any math or physics you could have done using cross products can be done more easily and more logically using a wedge product instead.
The scalars in Clifford algebra are the familiar real numbers. They obey the familiar laws of addition, subtraction, multiplication, et cetera. Multiplication of scalars is commutative and distributes over addition.
The vectors in Clifford algebra can be added to each other, and can be multiplied by scalars in the usual way. We will introduce multiplication of vectors in section 1.5.
Presumably you are familiar with the idea of adding scalars to scalars, and adding vectors to vectors (tip to tail). We now introduce the idea that any element of the Clifford algebra can be added to any other. This includes adding scalars to vectors, adding vectors to bivectors, and every other combination. So it would not be unusual to find an element C such that:
| C = s + V + B (1) |
where s is a scalar, V is a vector, and B is a bivector.
This clearly sets Clifford algebra apart from ordinary algebra.
Remark: Sometimes non-experts find this disturbing. Adding scalars to vectors is like adding apples to oranges. Well, so be it: people add apples to oranges all the time; it’s called fruit salad. In contrast, it is proverbially unwise to compare apples to oranges, and indeed we will not be comparing scalars to vectors. Addition (s + V) is allowed; comparison (s < V) is not.
Terminology: The most general element of the Clifford algebra we will call a clif. In the literature, the same concept is called a multivector, but we avoid that term because it is misleading, for reasons discussed near the end of section 1.9.
Presumably you already know how to add vectors graphically, by placing them tip-to-tail as shown in figure 2. By extending this idea, we can also add bivectors graphically, by placing them edge-to-edge as shown in figure 3.
As a concrete example of addition of bivectors, consider a gyroscopic precession problem, as follows: The green bivector is the initial angular momentum of the system, and the small purple bivector is torque*time. Then the yellow bivector is the new angular momentum, which has a new orientation due to precession.
Given any clif C, we can talk about the grade-0 piece of it, the grade-1 piece of it, et cetera.
Notation: The grade-N piece of C is denoted ⟨C⟩N.
We will often be particularly interested in the scalar piece, ⟨C⟩0.
Note: If you are familiar with complex numbers, you can understand the ⟨⋯⟩ operator as analogous to the ℜ() and ℑ() operators that select the real and imaginary parts. However, there is one difference: By definition, ℑ(z) is a real number, for any complex z, whereas ⟨C⟩2 is a bivector (or zero) for any clif C. See reference 1 for more on this.
We postulate that there is a geometric product operator that can be used to multiply any element of the Clifford algebra by any other.
Notation: The geometric product of A and B is written AB. That is, we simply juxtapose the multiplicands, without using any operator symbol.
The geometric product is associative and distributes over addition:
| (2) |
where A, B, and C are any clifs.
As a special case of the geometric product, multiplying scalars by scalars is straightfoward. This is just the familiar multiplication of real numbers. In this case, multiplication is commutative.
As another special case, multiplying vectors by scalars is also straightforward, and is presumably familiar from ordinary vector algebra. This is another case where multiplication is commutative; that is, sV = Vs for any scalar s and any vector V.
For that matter, it is easy to multiply any clif by a scalar. This is always commutative; that is, sC = Cs for any scalar s and any clif C.
We have already asserted that any clif can be multiplied by any other clif. Multiplying a vector by a vector is a particularly interesting case. At this point Clifford algebra makes a dramatic departure from ordinary vector algebra.
Given two vectors P and Q, we know that the geometric product PQ exists, but (so far) that’s about all we know. However, based on this mere existence, plus what we already know about addition and subtraction, we can define two new products, namely the dot product P·Q and the wedge product P∧Q, as follows:
| (3) |
Keep in mind that in the formula P∧Q=(PQ−QP)/2 we are assuming both P and Q are vectors (grade=1). This is a very useful formula, but you should become overly attached to it, because it doesn’t work for higher (or lower) grades. See section 1.10 for a more general formula.
Along almost-similar lines, the formula P·Q=(PQ + Q)/2 works for any combination of vectors and/or scalars (grade≤1). See section 1.11 for a more general formulas.
As an immediate corollary of equation 3, we can re-express the geometric product of two vectors as:
| PQ = P·Q + P∧Q (4) |
Again we emphasize that this useful formula only works when both P and Q are vectors. I keep mentioning this, because some authors take equation 4 to be the “definition” of geometric product (based on some sort of pre-existing notion of dot and wedge). They can get away with that for the product of two plain old vectors, but it fails for higher (or lower) grades, and creates lots of confusion.
Another corollary is that the dot product of two vectors is symmetric, while the wedge product is antisymmetric:
| (5) |
Let’s investigate the properties of the dot product. We restrict attention to ordinary grade=1 vectors. We will show that the dot product defined here behaves just like the dot product you recall from ordinary vector algebra. For starters, we are going to argue that P·P behaves like a scalar.
One characteristic behavior of a scalar (in the geometric sense) is that if you rotate it, nothing happens. This is very unlike a vector, which changes if you rotate it (unless the plane of rotation is perpendicular to the vector).
As an introductory special case, consider rotating P by 180 degrees, assuming P lies in the plane of rotation. That’s easy to do: a 180 degree rotation transforms P into −P. We are pleased to see that this transformation leaves P·P unchanged.
It’s also obvious that a rotation in a plane perpendicular to P leaves P·P unchanged, which is reassuring, although it doesn’t help distinguish scalars from anything else.
Tangential remark: More generally, we assert without proof that P·P is in fact invariant under any rotation (i.e. any amount of rotation in any plane). We are not ready to prove this, since we haven’t yet formally defined what we mean by rotation ... but we will pretty much insist that rotation leave P·P invariant, because we want P·P to be a scalar, and we want √(P·P) to be the length of P, and we want rotations to be length-preserving transformations. (This isn’t a proof, but it is an argument for plausibility and self-consistency.)
If P·P is a scalar, it is easy to show that P·Q is a scalar, for any vectors P and Q. Just define R := P + Q and then take the dot product of each side with itself:
| R·R = P·P + 2 P·Q + Q·Q (6) |
where every term except 2 P·Q is manifestly a scalar, so the remaining term must be a scalar as well.
This leaves us pretty much convinced that the dot product between any two vectors is a scalar. It can’t be a vector or anything else we know about. To get here, we didn’t do much more than postulate the existence of the geometric product, and then do a bunch of arithmetic.
Terminology: If vector Q is equal to P, or is equal to P multiplied by any nonzero scalar, we say that P and Q are parallel and we symbolize this as P ∥ Q.
Based on what we already know (mainly the symmetry properties, equation 5) we can deduce that if P and Q are parallel, then P∧Q = 0 and PQ = P·Q; that is:
| PQ = QP = P·Q iff P ∥ Q (7) |
which gives us a useful test for detecting parallel vectors.
Terminology: If P·Q = 0, we say that vectors P and Q are perpendicular or equivalently orthogonal and we symbolize this as P ⊥ Q.
If vectors P and Q are orthogonal, then P·Q = 0 and PQ = P∧Q; that is:
| PQ = −QP = P∧Q iff P ⊥ Q (8) |
In general, in the case where P and Q are not necessarily parallel or perpendicular, the geometric product will have two terms, in accordance with equation 4.
Lemma: We can resolve any vector P into a component PQ which is parallel to vector Q, plus another component (P−PQ) which is perpendicular to Q. Proof by construction:
| PQ := Q |
| (9) |
This lemma is conceptually valuable, and frequently useful in practice. (See e.g. section 1.17.)
It is an easy exercise to show the following:
| (10) |
Now, let’s investigate the properties of the wedge product of two vectors. We anticipate that it will be a bivector. We use the same line of reasoning as in section 1.7. We assume P∧Q is nonzero.
You can easily show that the wedge product P∧Q is invariant with respect to 180 degree rotation in the PQ plane. That is, just replace P by −P and Q by −Q and observe that nothing happens to the wedge product. This tells us the product is not a vector in the PQ plane. We remark without proof that this result is invariant under any rotation (however small or large) in the PQ plane.
Things get more interesting if we have more than two dimensions, because that allows us to investigate additional planes of rotation.
To make things easy to visualize, let us replace Q by Q’, where Q’ is the projection of Q in the directions perpendicular to P. We can always do this, using the methods discussed in section 1.8. According to equation 10, we know P∧Q’ is equal to P∧Q.
Choose any vector R perpendicular to both P and Q’. Rotate both vectors in the PR plane by 180 degrees. This transforms P into −P, but leaves Q’ unchanged (since it is perpendicular to the plane of rotation). That means the rotation flips sign of the wedge product, P∧Q.
Similarly a rotation in the QR plane flips the sign of the wedge product. As a final check, we perform an inversion, i.e. the operation that transforms any vector V into −V, not limited to any plane of rotation. This leaves the wedge product unchanged.
Taking all these observations together, we find that P∧Q behaves exactly as we would expect a bivector to behave, based on the description given in section 1.1: a patch of surface with a direction of circulation around its edge. That is: the area is unchanged if we rotate things in the plane of the surface, but if we rotate things 180 degrees in a plane perpendicular to the surface, the surface flips over, reversing the sense of circulation.
The idea of wedge product generalizes to more than two vectors. For example, with three vectors, we generalize equation 3 as follows:
| P∧Q∧R := |
| (PQR + QRP + RPQ − RQP − QPR − PRQ) (11) |
You can skip the following equation if you’re not interested, but if you want the fully general expression, it is:
| q1∧q2∧q3⋯qr := |
|
| sign(π) qπ(1) qπ(2) qπ(3)⋯ qπ(r) (12) |
where the sum runs over all possible permutations π. There are r! such permutations, and sign(π) is defined to be +1 for even permutations and −1 for odd permutations. This will be an object of grade r if all the vectors q1⋯qr are linearly independent; otherwise it will be zero.
Terminology: A blade is defined to be any scalar, any vector, or the wedge product of any number of vectors.
Terminology: Any clif that has a definite grade is called homogeneous. It is necessarily either a blade or the sum of blades, all of the same grade.
Example: In four dimensions, the quantity γ0 γ1 + γ2 γ3 is homogeneous but is not a blade. It has grade=2, but cannot be written as just the wedge product between two vectors.
Terminology: As previously mentioned, we use the term clif to cover the most general element of the Clifford algebra. In the literature, the same concept is called a multivector, but we avoid that term because it is misleading. The problem may be due in part to the etymology suggested by the sequence:
| vector, bivector, trivector, ⋯, multivector (WRONG) (13) |
in contrast to the correct sequence:
| vector, bivector, trivector, ⋯, blade (RIGHT) (14) |
Terminology: Do not confuse a trivector with a 3-vector. A trivector is visualized as the 3-dimensional region spanned by three vectors. This region may be embedded in a space that is 3-dimensional or higher. In contrast, a 3-vector is a single vector that lives in a 3-dimensional space.
Terminology: A bivector can be called a 2-blade. A trivector can be called a 3-blade. And so on.
So far we have only defined the wedge product as acting on vectors. We can generalize it so that we can take the wedge product between any blade and any blade, simply by saying the wedge product is associative:
| (15) |
where the RHS is defined by equation 12.
It is easy to see that for any two blades P and Q, which are of grade p and q respectively, the grade of P∧Q will be p+q (unless the product vanishes entirely, i.e. P∧Q=0).
We can use that idea in the other direction, as follows: As discussed in section 1.13, the full geometric product PQ is liable to contain terms of all grades from |p−q| to p+q inclusive (counting by twos). The wedge product consists of just those terms with the highest possible grade. In symbols:
| (16) |
Given this definition of blade wedge blade, we can generalize to any clif wedge clif, simply by saying the wedge product distributes over addition:
| V∧(A + B) = V∧A + V∧B (17) |
We hereby define the dot product of two blades to be the lowest-grade part of the geometric product. That is, if P has grade p and Q has grade q, then the dot product will have grade |p−q|. In symbols:
| (18) |
Just as the wedge product was the top-grade part of the geometric product, the dot product is the bottom-grade part.
Let’s be clear: The definition of dot product depends more on its grade than on its symmetry. The dot product of two vectors is symmetric: V·W=W·W while the dot product of a vector with a bivector is antisymmetric: V·B=−B·V.
You can check that this more-general definition of dot product is consistent with what we said back in section 1.6 about the dot product of vectors.
Given this definition of blade dot blade, we can generalize to any clif dot clif, simply by saying that the dot product distributes over addition. That is,
| V·(A + B) = V·A + V·B (19) |
There is a very interesting way to visualize the wedge product. Consider the product C∧V, where C is a clif of any grade and V is a vector. The idea is to use C as a paintbrush, dragging C along V. The dragging motion is specified by the direction and magnitude of V. We keep C parallel to itself during the process. For instance, in figure 1 or figure 4, we form the parallelogram P∧Q by dragging the vector P along Q. Similarly in figure 1 we form the parallelepiped P∧Q∧R by dragging the parallelogram P∧Q along R.
The paintbrush picture is a little dodgy in the case where C is a scalar, but we can repair it by rewriting s∧V as 1∧(sV), for any scalar s. That is, we take the scalar 1 (which is pointlike) and drag it for a distance |sV| in the V direction. It just paints a copy of sV.
The orientation of the bivector P∧Q can be thought of as a “direction of circulation” marked on the parallelogram, namely moving in the P direction then moving in the Q direction. In figure 4, Q∧P = − P∧Q because they have the opposite direction of circulation. (They have the same magnitude, just opposite orientation.)
Important note: The following three concepts are all optional, and are all equivalent: (1) A notion of “front” versus “back” side of the bivector; (2) a notion of chirality such as the “right-hand rule”; and (3) a notion of “clockwise” circulation.We emphasize that we have not defined any of these three concepts. We are just saying that if you did define them, they would all be equivalent. We are not going to rely on any notion of clockwise or right-handedness or front-versus-back. Instead, we rely on orientation as specified by circulation around the edge of the bivector, which is completely geometrical and completely non-chiral.
We make a point of keeping things non-chiral, to the extent possible, because it tells us something about the symmetry of the fundamental laws of physics, as illustrated in reference 2.
In general, if you multiply an object of grade r by an object of grade s, the geometric product is liable to contain terms of all grades from |r−s| to |r+s|, counting by twos.
Example: Let {γ1, γ2, γ3, γ4} be a set of orthonormal spacelike vectors, as discussed in section 1.17. Let A := γ1∧γ2, and let B := (γ2 + γ3)∧(γ4 + γ1). Both A and B are homogeneous of grade 2. Indeed they are 2-blades. It is easy to calculate the geometric product AB. Show that ⟨AB⟩0 is nonzero, ⟨AB⟩2 is nonzero, and ⟨AB⟩4 is nonzero. Hint: ⟨AB⟩4 = γ1 γ2 γ3 γ4.
For high-grade clifs A and B, the geometric product AB generally leaves us with a lot of terms. As discussed in section 1.11 the bottom-grade term is the dot product ... and as discussed in section 1.10, the top-grade term is the wedge product. Alas, the other terms don’t have any such special names.
If we temporarily restrict attention to plain old vectors (grade=1 only), we reach the remarkable conclusion that the geometric product of two vectors has only two terms, a scalar term and a bivector term (assuming the bivector term is nonzero):
| (20) |
which we can compare and contrast with equation 3, which we reproduce here
| (21) |
still assuming V and W are vectors.
Sometimes one sees introductory discussions that start by presenting the properties of the dot product and wedge product, and then “define” the geometric product as
| VW := V·W + V∧W (allegedly) (22) |
which turns the discussion on its head relative to what we have done here. We started by postulating the existence of the geometric product, and then used it to work out the properties of dot and wedge.
They can get away with equation 22 when talking about vectors, but it doesn’t generalize well to higher-grade objects, and it gets students started off on the wrong foot conceptually.
In ordinary Euclidean space, whenever you compute the dot product of a vector with itself, the result is positive; that is, S·S > 0. In general, whenever this dot product is positive, we say that the vector S is spacelike.
In special relativity, i.e. in Minkowski space, we find that some vectors have the property that T·T < 0. In that case, we say that the vector T is timelike.
In a space where spacelike and timelike vectors exist, there will be other vectors with the property that N·N = 0. We say that such a vector N is null or equivalently lightlike.
I define the gorm of a vector to be dot the product of a vector with itself. The gorm is bilinear, unlike the norm which is linear. For a spacelike vector, the norm is √(S·S), and corresponds to the notion of proper length. Meanwhile, for a timelike vector, the norm is √(−T·T), which corresponds to the notion of proper time interval. For a null vector, the norm is zero.
For a more general definition of gorm, see section 1.16.
We define the reverse of a clif as follows: Express the clif as a sum of products, and within each term, reverse the order of the factors. For example, the reverse of (P + Q∧R) is (P + R∧Q), where P, Q, and R are vectors (or perhaps scalars).
Notation: For any clif C, the reverse of C is denoted C∼
Reverse has no effect on individual scalars or vectors, but is important for bivectors and higher-grade objects. Reverse plays an important role in the description of rotations, as discussed in reference 3. It also appears in the general definition of gorm, as discussed in section 1.16
Note: If you are familiar with complex numbers, you can understand the reverse as a generalization of the notion of complex conjugate. See reference 1 for details.
In all generality, the gorm of any clif C is formed by multiplying C by the reverse of C, and keeping the scalar part of the product. That is:
| gorm(C) := ⟨C∼ C⟩0 (23) |
For example, if C = a + b γ1 + c γ2 + d γ1 γ2, then the gorm of C is a2 + b2 + c2 + d2 ... assuming γ1 and γ2 are spacelike basis vectors, as discussed in section 1.17. You can almost consider this a generalization of the Pythagorean formula, where in a non-abstract sense γ1 is perpendicular to γ2, and in some much more abstract sense the terms of each grade are “orthogonal” to the terms of every other grade.
Given any set of d linearly-independent non-null vectors, we can create an orthornormal basis set, i.e. a set of d mutually-orthogonal unit vectors. Actually we can create arbitrarily many such sets.
Proof by construction: Use the Gram-Schmidt orthonormalization algorithm. That is, use formulas like equation 9 to project out mutually-orthogonal components. Then divide by the norm to normalize them.
In Minkowski spacetime, any such basis will have the following properties:
| γ0 γ0 = −1 (24) |
| γ1 γ1 = γ2 γ2 = γ3 γ3 = +1 (25) |
and
| γi γj = − γj γi for all i ≠ j (26) |
In this basis set, γ0 is the timelike unit vector, while γ1, γ2, and γ3 are the spacelike unit vectors.
Remark: The minus sign in equation 24 stands in contrast to the plus sign in equation 25. This one difference in signs is essentially the only thing that sets special relativity apart from ordinary Euclidean geometry. This point is discussed more fully in reference 4.
In ordinary Euclidean space, the story is the same, except there are no timelike vectors, so you simply forget about γ0 and equation 24.
Given a basis, we can write any arbitrary vector V as a linear combination of the basis vectors:
| V = a γ0 + b γ1 + c γ2 + d γ3 (27) |
for suitable scalars a, b, c, and d.
Terminology: These scalars (a, b, c, and d) are sometimes called the components of V in the chosen basis. They can also be called the matrix elements of V in the chosen basis.
Terminology: The vector a γ0 is sometimes called the component of V in the chosen γ0 direction (and similarly for the other terms on the RHS of equation 27). Such a vector can also be called the projection of V onto the chosen directions.
It is usually obvious from context which definition of “component” is intended. If you want to avoid ambiguity in your writing, you can avoid the word “component” and instead say “matrix element” or “projection” as appropriate.
We can also write the expansion of V as
| V = V0 γ0 + V1 γ1 + V2 γ2 + V3 γ3 (28) |
where again the Vi are called the components (or matrix elements) of V in the chosen basis.
Beware: Even though Vi is a component of the vector V and is a scalar, please do not think of γi in the same way. Each γi is a vector unto itself, not a scalar. The i in γi tells which vector, whereas the i in Vi tells which component of the vector. There is no advantage in imagining some super-vector that has the γi vectors as its components.
Given two vectors P and Q, the dot product can be expressed in terms of their components as follows:
| P·Q = −P0 Q0 + P1 Q1 + P2 Q2 + P3 Q3 (29) |
assuming timelike γ0 and spacelike γ1, γ2, and γ3.
Note that this is not the definition of dot product; it is merely a consequence of the earlier definition of dot product (equation 4) and the definition of components (equation 29).
In particular: Non-experts sometimes think the dot product is “defined” by adding up the product of corresponding components, but that is not true in general, as you can see from the minus sign in front of the first term in equation 29. The bogus definition is reinforced by software library routines that compute a so-called “dot product” by blithely multipling corresponding elements. (If all the basis vectors are spacelike, then you can get away with just multiplying the corresponding components, but keep in mind that that’s not the definition, and not the general rule.)
Useful tutorials on various aspects of Clifford algebra and its application to physics include reference 5, reference 6, and reference 7.
The number of components required to describe a clif depends on the number of dimensions involved. The first few cases are shown in this table:
| (30) |
where s means scalar, v means vector, b means bivector, t means trivector, and q means quadvector. You can see that it takes the form of Pascal’s triangle. On each row, the total number of components is 2D.
When we speak of “the” dimension, it refers to the dimensionality of whatever space you are actually using. This includes the case where, for whatever reason, attention is restricted to some subspace of the natural universe. For example, if your universe contains three dimensions, but you are only considering a single plane of rotation, then the D=2 description applies. Similarly, if you live in four-dimensional spacetime, but are only considering rotations in the three spacelike directions, then the D=3 description applies.
To say the same thing another way, Clifford algebra is remarkably agnostic about the existence (or non-existence) of dimensions beyond the ones you are actually using. (This makes the geometric product much more elegant than the old-fashioned vector cross product, which requires you to think about a third dimension, even if you only started out with two dimensions.)
If you find that you need D dimensions to describe the laws of physics, that sets a lower bound on the dimensionality of the universe you live in. It is not an upper bound, i.e. it provides not the slightest evidence against the existence of additional, unseen dimensions, such as arise in string theory.
There are always multiple ways of presenting the same material. In the case of Clifford algebra, it would have been possible to leap to the idea of a basis set very early on. The sequence would have been: (a) establish a few fundamental notions; (b) set forth the behavior of the basis vectors according to equation 25 and equation 26; (c) express all vectors, bivectors, etc. in terms of their components relative to this basis; and (d) derive the main results in terms of components. Let’s call this the basis+components approach.
Some students prefer the basis+components approach because it is what they are expecting. They think a vector, by definition, is nothing more than a list of components.
The alternative is to think of a vector as a thing unto itself, as an object with geometric properties, independent of any basis. Let’s call this the geometric approach.
We must ask the question, which approach is more elementary, and which approach is more sophisticated? Also, which approach is more abstract, and which approach is more closely tied to physical reality?
Actually those are trick questions; they look like dichotomies, but they really aren’t. The answer is that the geometric approach is more physical and more abstract. It is more elementary and more sophisticated.
| You can use a pointed stick as a physical model of a vector, independent of any basis. Wave it around in front of the class. | Show how vectors can be added by putting them tip-to-tail. |
| Use a flat piece of cardboard as a physical model of a bivector. | Show how bivectors can be added by putting them edge-to-edge. |
In physics, almost everything worth knowing can be expressed independently of any basis. You should be suspicious of anything that appears to depend on a particular chosen basis. For more about this, see reference 8. Observe that everything we did in section 1 was done without reference to any basis; we made a point of postponing the definition of “basis” and “components” until the very end.
The real practical advantage of the basis+components approach is that it is well suited for numerical calculations, including computer programs. Reference 3 includes a program that is useful for keeping track of compound rotations in D=3 space.
Consider the contrast:
| The geometric approach is physical yet algebraic, axiomatic, and abstract; it is elementary yet sophisticated. | The basis+components approach is more numerical, i.e. more suited for computer programs. |
Some students have prior familiarity with one approach, or the other, or both, or neither.
The cross product only makes sense in three dimensions, because the result points in “the” direction perpendicular to the two multiplicands. In two dimensions, there cannot be any such direction, and in four dimensions (or higher), there is an infinitude of directions perpendicular to any two vectors, so talking about “the” perpendicular direction is so underspecified as to be meaningless. In contrast, the wedge product is well defined and well behaved in all dimensions from two dimensions on up.
The cross product is defined in terms of a “right hand rule”. In contrast, a wedge product is well defined without any notion of handedness, without any notion of chirality. This is more important than it might seem, because it changes how we perceive the apparent symmetry of the laws of physics, as discussed in reference 2.
| ∇ F = |
| J (31) |
It is worth learning Clifford algebra just to see this equation. For details, see reference 9.
Also: In their traditional form, the Maxwell equations seem to be not left/right symmetric, because they involve cross products. However, we believe that classical electromagnetism does have a left/right symmetry. By rewriting the laws using geometric products, as in equation 31, it becomes obvious that no right-hand rule is needed. A particularly pronounced example of this is Pierre’s puzzle, as discussed in reference 2.
Similarly: The traditional form of the Maxwell equations is not manifestly invariant with respect to special relativity, because it involves a particular observer’s time and space coordinates. However, we believe the underlying physical laws are relativistically invariant. Rewriting the laws using geometric products makes this invariance manifest, as in equation 31.
As an elegant application of the basic idea that the electromagnetic field is a bivector, reference 10 explains why a field that is purely an electric field in one reference frame must be a combination of electric and magnetic fields when observed in another frame.
As a more mathematical application of equation 31, reference 11 calculates the field surrounding a long straight wire.
