This book is a trap. It is superficially attractive, but the more you
step into it, the more it reveals itself to be a morass of wrong
physics and bad pedagogy. The book contains some good ideas,
but they are so diluted by bad ideas that nothing can be relied upon.
This makes the book particularly unsuitable for its target audiences,
namely preservice teachers and novice teachers (part I) or students
(part III).
The book pays lip service to lofty principles, such as the importance
of critical thinking, sensitivity to student misconceptions, and the
precedence of ideas over terminology. Alas the book by-and-large
fails to uphold those principles. An example is its mishandling of
the two-fluid theory of electrical charge (item 24).
The book is too much in thrall to the “historical approach”,
resulting in needless complexity, confusion, and error. See
section 4.
The book goes out with a bang. Chapters III-3 and III-4 are a long
discussion of thermodynamics without entropy ... which is like skydiving
without a parachute. The book mentions heat, sensible heat, latent
heat, caloric, friction, and energy ... without ever mentioning
entropy. Ideas such as spontaneity and irreversibility that are
intimately connected with entropy are almost-explicitly attributed to
energy instead. Also the student is led by detailed historical
arguments to a wrong theory, namely conservation of caloric. This
will have to be unlearned later. Unlearning is never easy. See
item 45.
A relatively minor additional criticism is that the book is
inconsistent as to level. It purports to discuss introductory
physics, yet it sometimes complains that conventional courses leave
students with an incomplete understanding of difficult topics. That’s
silly, since incompleteness is natural and unavoidable in an
introductory course. For example, see item 32.
For some possibly-constructive suggestions on how to deal with
misconceptions in the classroom, see reference 1.
In what follows, approving comments are marked (+) and disapproving
comments are marked (–).
-
- 1.
(–) On page I-23: It defines «velocity» in an unconventional and
unwise way, and then spends several pages explaining how problematic
that is. It’s a straw-man argument. If you define velocity in the
usual way, it’s not problematic.
- 2.
(+) On page I-46: The book rightly recognizes Galileo’s role as the
father of modern science. This includes the idea that even when
physics says what will happen, it need not (and often does not)
say why it happens. This needs to be emphasized, because it
is important and because it is not obvious to students.
- 3.
(+) On page I-65: PSSC Physics is rightly praised for a
«simple, correct, and consistent presentation suitable for
introductory levels.»
- 4.
(–) On page I-67: It says we «would do better to redefine weight as
occasion arises».
I don’t mind making approximations, especially in an introductory
course, but to repeatedly redefine the meaning of a single term,
back and forth – not just in the direction of progressive refinement
– is a very bad practice. It would be much better to put qualifiers
on the various versions, such as the subscripts on gI, gL, and
gE as explained in reference 2.
In Teaching Introductory Physics, the definition of mg on page I-16 contradicts the definition
on page I-66 which contradicts the definition on page I-126.
- 5.
(–) On page I-76: It talks about teaching students to distinguish
«active» versus «passive» forces. When 700 physics teachers were
asked about this, not one thought it was a good idea. Some students
spontaneously make such a distinction, but they should be encouraged
to discard it.
The fact is, the laws of physics do not care whether a force is
«active» or «passive». There are innumerable examples of forces
that cannot meaningfully be classified as «active» or «passive».
- 6.
(–) On page I-85ff: The discussion of weightlessness is a disaster.
It misunderstands Einstein’s principle of equivalence, namely that
the definition of g and hence the definition of weight are
frame-dependent. They do not depend on the state of motion of
the observed object, but rather on the state of motion of the
observer’s frame of reference.
Students enter with a qualitative but perfectly correct notion that
astronauts are weightless in the frame comoving with the space
station. It would be foolish to force them to unlearn this idea in
the introductory class, and then force them to relearn it later.
- 7.
(–) On page I-92: The section title says «Objects are not
“thrown backwards” when accelerated». This is bad pedagogy for two
reasons. First of all, it is suboptimal to talk about what doesn’t
happen; it would be better to talk about what does happen. Secondly,
this continues the practice of not honoring the principle of “idea
before name”, in the sense that the title deflects attention from
something important to something hardly worth discussing. There are
two simple ideas here, and the crucial first step, the sine-qua-non, is to
keep track of which idea you are talking about, which the book fails
to do.
-
If the object is accelerated forward,
what happens to the object? Well, duh, it accelerates forward.
- If the reference frame is accelerated forward, what happens to a
free object? It accelerates backward relative to that frame.
It is a great disservice to students to teach them the equivalence
principle one day and then penalize them for invoking the principle
another day.
This is an example where the book compounds a misconception rather
than dispelling it.
- 8.
(+/–) On page I-97: This is a Jekyll-and-Hyde passage. I agree that
there is an important distinction between an equation and a
definition. But replacing the = sign with the ≡ sign is not
a good solution to the problem, because the ≡ sign is too
symmetric. Equality is symmetric, but definitions are not symmetric.
It is much smarter to use the := sign for definitions, writing
A:=B when A is being defined in terms of B.
The same issue shows up again on page I-185.
- 9.
(–) On page I-97: It says «The equals sign in Fnet = ma is
not just an ordinary functional equality. it conceals the combination
of arbitrary definition and laws of nature....» I’m pretty sure that
is not true. It would be unconventional to define net force in
terms of mass times acceleration (especially since that would leave us
stuck with the task of defining non-net forces). This would
contradict the operational definition of force offered by PSSC,
which Teaching Introductory Physics seems to endorse. Conversely, it would be absurd to
define mass times acceleration in terms of force. Furthermore, there
is no reason why «laws of nature» such of this cannot be expressed
in terms of plain old equations. Also I do not know what «functional
equality» means in this context; I cannot imagine how it differs from
any other kind of equality.
- 10.
(+) On page I-108: Yes, students should practice adding vectors
graphically, tip-to-tail.
- 11.
(–) On page I-108: This makes the point that rotations are not well
represented by vectors, but fails to suggest how they should be
represented. (Hint: bivectors will do nicely. See reference 3.)
- 12.
(+) On page I-107: The mention of «additive inverse» in
connection with subtraction is always a good idea. Specifically,
when introducing vector subtraction, it is a particularly good idea.
(More generally, an introductory physics course must review many ideas
that are directly connected to the axioms of arithmetic, and it helps
to be explicit about the connection.)
- 13.
(+) On page I-108: The point is well made that «vectors are
not tied to points». Textbooks often gloss over this important point.
- 14.
(–) On page I-109: This needlessly tramples the distinction
between a vector and the components of the vector.
Vectors exists as geometric objects, whether or not we evaluate
their components relative to this-or-that reference frame.
See reference 4.
- 15.
(–) On page I-117: Although radian measure is conventional in
some situations, it is not «natural». It is not even conventional
in all situations. Using radians per second is not more
«natural» than using Hz.
- 16.
(–) On page I-118: The cosine formula is wrong. It needs repairs in two
places.
- 17.
(+/–) On page I-119ff: The discussion of circular motion makes some
good points, but sometimes gets quite muddled. The section on
centrifugal force discusses all possible views of the subject, to the
point where I don’t know what is being espoused and what is being
deprecated.
- 18.
(–) On page I-125: After spending many pages trying to set up a
formalism that treats circular motion without the use of centrifugal
force, we suddenly get a string of problems that practically beg to
be analyzed using the rotating frame of reference, i.e. where the
students have every reason to put themselves in the role of observers
in the accelerated frame.
- 19.
(–) On page I-127: In the passage on fictitious forces, it is
particularly unclear what is being espoused and what is being
deprecated.
- 20.
(–) On page I-129 and 130: It repeatedly fails to make the important
distinction between the tidal stress and the observed height of
the tide. It takes for granted that the observed tide is
«semidiurnal», which is simply not the case. See
reference 5.
- 21.
(–) On page I-142: It takes an unjustifiably narrow view of what “heat”
means. It deprecates the idea of «converting work into heat» even
though such terminology has been used in the technical thermodynamic
literature uninterruptedly since 1798 (reference 6). See
reference 7 for more discussion of the various things “heat”
can mean.
- 22.
(–) On page I-146: It introduces the «first law» (of thermodynamics)
in the form
which is not a valid equation, because there is no function Q and no
function W that could possibly mean what equation 1
requires them to mean.
Furthermore, even if we were to cross out equation 1
and insert something roughly similar that actually means something,
such as
this would still be highly suboptimal, because equation 2
is nowhere near general enough to deserve being called the «first
law» of anything. It would be much better to formulate the first law
of thermodynamics as a simple, direct statement of conservation of
energy, as discussed in reference 7.
Compare item 56.
- 23.
(–) On page I-148: It alleges that the change in energy can be
expressed as «the algebraic sum of the various different internal
energy changes»
|
ΔE = ΔEtherm + ΔEchem + ΔEkin + ΔEpot + ⋯
(3) |
A similar equation appears on page III-128.
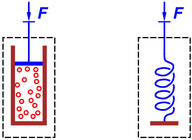
Let’s see if we can apply this equation to the mechanisms shown in
figure 1. The mechanism on the right side of the figure
contains just a simple spring. Any F·dx work done by the
applied force will presumably result in macroscopic potential energy
stored in the spring, and attributed to the ΔEpot term in
equation 3. So far so good.
Meanwhile, the mechanism on the left side of the figure contains
a gas of anhydrous acetic acid molecules. If we temporarily (!)
approximate this as an ideal gas, any F·dx work done by the
applied force will result in kinetic energy in the gas molecules.
So arguably this should be attributed to the ΔEkin term in
equation 3. But since it is microscopic kinetic
energy, not center-of-mass kinetic energy, arguably it should be
attributed to the ΔEtherm term. Furthermore, if we look more
closely, we see that the acetic acid molecules undergo a reversible
chemical reaction, to an extent that depends on pressure, so this
is not really an ideal gas, and some of the F·dx work
should be attributed to the ΔEchem term. On the other hand,
the energy of chemical bonds is entirely attributable to the potential
and kinetic energy of the electrons and nuclei in the molecule, so
arguably this should be attributed to the ΔEpot and ΔEkin terms
in equation 3.
Overall, I have no idea how to make the RHS of equation 3
meaningful. It appears to be mixing things that ought not to be
mixed.
- 24.
(–) On page I-173, 175, 177, 184, and elsewhere: It says there are
«two distinct “varieties” of charge» .... «The choice of the
“two distinct varieties” is eventually forced on us by
microscopic rather than macroscopic phenomena.» It says that
Franklin’s one-fluid model is «fallacious».
That’s just wrong physics. Charge is not matter, and matter is not
charge. Electrons and protons are different kinds of charged
particles, but they are not the only kinds of particles, and all
together there is only one kind of electrical charge. We know how
things would look if there really were multiple kinds of charge, by
analogy to the nuclear color charge — and electrical charge
definitely does not look like that. See
reference 8 for details on this.
This is the height of irony: The book preaches “critical thinking”
at every opportunity, yet it repeatedly and emphatically rejects the
one-component theory, even though there has never been the slightest
evidence against the theory.
- 25.
(–) On page I-199: I don’t understand the emphasis on batteries and
bulbs to the exclusion of voltmeters.
- 26.
(–) On page I-203: It says «Joule’s law should be recognized as
having an essentially independent status». I have no idea what that
means. Independent of what?
- 27.
(–) On page I-204: The footnote gives a hopelessly muddled
discussion of what “voltage” means. It dances around the issue of
electrostatic gauge invariance without properly dealing with the
issue. Sometimes it is useful to assign a voltage to a point in
a circuit.
- 28.
(–) On page I-204: The footnote implies that “voltage” and
“potential” are synonymous, which is not the case, as can be proven
by glancing at a betatron.
- 29.
(–) On page I-213/214: It says «one could,
in principle, find the molecular mass µ of the gas from the
measurable quantities since on obtains:
where Δp represents the pressure....»
Molecular mass? Really?
It goes on to say «Although this is certainly not a useful way of
measure molecular mass, able students find the exercise in mathematical
physics very instructive.»
Calling it not «useful» is beyond an understatement.
Equation 4 cannot possibly measure the molecular mass
at all. This should be obvious on theoretical grounds. It should
also be obvious from an order-of-magnitude estimate for the quantities
involved, considering (say) a 1000-foot-high column of air subject to
a one-Gee acceleration.
- 30.
(–) On page I-229: Referring to some of Faraday’s
hypotheses, it says «The fact that one might perhaps take issue with
some of these views and rationalize the observations in some other way
is not the point.» Well, it should be the point. We should
critically evaluate the evidence, even if Faraday didn’t.
The book touts the importance of critical thinking, but fails to
follow its own advice. The historical tail is allowed to wag the
thoughtful dog.
See section 4 for more on this.
- 31.
(–) On page I-249: It says «The three preceding derivations of
wave propagation velocity have been deliberately designed to dramatize
the power of an identical approach applied to seemingly very different
physical situations.»
There seems to be some dramatic license involved. The approach that
works for pressure waves in a tube of air doesn’t work for strings.
The calculation on page I-243 only works for a particular chosen point
on a particular chosen waveform; the main features
(e.g. dispersionless propagation) of waves on a string were
assumed on page I-242. They were assumed without proof, not
derived.
- 32.
(–) On page I-257: It correctly points out that «Like many other
phenomena impinging on immediate experience ... diffuse reflection is
very complex.» It then goes on to complain that «Since students are
rarely, if ever, asked to sketch diagrams in which they themselves
show the multiplicity of rays emerging from each point on the object
and then select a preferred ray for further tracing, they end up
without firm assimilation of the concept.» Well, I wouldn’t expect
them to firmly assimilate complex ideas in an introductory course.
It would rarely, if ever, be appropriate to require or expect this.
- 33.
(–) On page I-275: Replacing one half-truth with another is
nothing to be proud of. In the context of the Thomson cathode-ray
experiment, the book says «Many students (even graduate
students on qualifying examinations) respond that the gravitational
deflection is so small because the mass of the particles is so small.
They do not immediately invoke what they supposedly learned about the
uniformity of g for all objects, and they do not associate the
smallness of the [deflection] with the enormous velocity.»
This issue comes up again in question 14.8 in the book’s Section II.
Consider the contrast:
-
If the student fails to appreciate the enormous velocity,
then the student is half wrong.
- Since book fails to appreciate that
mass is a valid explanation under these conditions, the book is
half wrong in the other direction.
There is a scaling argument that goes like this:
|
½ m v2 | | = | | q V = constant |
| v2 | | ∝ | | 1/m |
| t | | = | | L/v | | distance = rate × time |
| | | ∝ | | |
| | | ∝ | | | | since L is constant |
| d | | ∝ | | t2 | | for any free fall |
| | | ∝ | | m
|
| (5)
|
Under the conditions of the experiment, the length of the apparatus
L is constant, the accelerating voltage V is constant, and the
charge of each particle q is the same. Therefore the velocity
scales inversely like the square root of the mass m, the time of
flight scales like the square root of the mass, and the gravitational
deflection d scales directly like the mass.
So I would not be too quick to pooh-pooh a student who says that the
small mass explains the small deflection. Even a student who cannot
articulate the details of the scaling argument might have a good
“feel” for the right argument … or might simply have
correctly identified the mass as the only parameter that could
possibly be relevant.
On the other hand, I would be disappointed if the student explained
the mass-dependence in a way that violated the equivalence principle,
or who thought the cathode ray velocity was small.
The book’s non-recognition of this scaling argument is inconsistent
with its remarks in Section 1.2 and elsewhere, which properly extol
the importance of scaling arguments.
- 34.
(–) On page I-286: It says «(This is not a matter of the complexity
of the idea; it is merely a matter of lack of practice on the part of
the students.)»
I disagree. It appears that the key idea here is the gauge
invariance of electrostatics. Students were not born knowing this
idea. Expecting students to re-invent gauge invariance on their own
is completely unreasonable. What’s more, depending on how the chassis
and vacuum-envelope of the apparatus are constructed, the ΔV
in this experiment may not even exhibit gauge invariance. I would say
that there are some quite «complex» ideas involved, and furthermore
the problem is seriously underconstrained, because the statement of
the problem leaves out important information. This goes far, far
beyond «lack of practice on the part of the students».
- 35.
(–) On page I-287: It seems that ΔV and
ΔVS are two different names for the same thing.
This just adds to the burdens imposed on the student by
item 34.
- 36.
(–) On page I-301: The discussion of special relativity places
far too much emphasis on Lorentz transformations. It places far too
little emphasis on four-vectors and spacetime diagrams. It thereby
passes up two opportunities: (1) to achieve a simpler yet more
profound understanding of relativity, and (2) to reinforce and deepen
the students’ understanding of ordinary vectors, geometry, and
trigonometry. See reference 9 and reference 10.
- 37.
(–) On page I-330: The whole discussion of «significant figures» is
a disaster, for reasons explained in detail in reference 11.
- 38.
(+/–) On page III-iii: It’s true that the usual
formulation of the second law of motion (and the work/KE theorem) is
only valid for point particles. And it’s true that the limitations
and provisos are often not adequately emphasized. On the other hand,
it is possible to lift some of these restrictions, as discussed in
reference 12.
- 39.
(–) On page III-22: The argument as to why impulse is
path-dependent is fundamentally unsound. The key question is not
asked, let alone answered. The question is, what would happen if we
chose a different path from state A to state B? The passage imparts
quite a serious misconception about what path-dependent means.
It is always possible, but meaningless, to find a
seemingly-path-dependent way of calculating a path-independent
quantity. See also item 48.
- 40.
(+) On page III-23: In the context of momentum and impulse, the
student is asked to «Show, from basic definitions, that kg m/s and
N·s are completely equivalent sets of units.» That is
interesting, because in the context of gravitation, there is a segment
of the PER community that insists on emphasizing the distinction
between m/s2 and N/kg.
- 41.
(–) On page III-4: When discussing one-dimensional motion, the
book says one vector is “positive” while another vector is
“negative”. Of course positive means greater than zero, and
negative means less than zero. So this leads to the equation
In equation 6, note that:
-
On the LHS there is a vector. The
vector v has an arrow over it to
emphasize that vectors are different from scalars.
- On the RHS there is a scalar.
- In the middle there is an inequality operator that is
generally only defined for scalars. Vectors are not well-ordered
(in two or more dimensions).
We should distinguish bad pedagogy from wrong physics. For
one-dimensional motion, this example does not count as wrong physics,
because in D=1 there is an isomorphism between scalars and vectors.
However, it certainly seems like bad pedagogy to emphasize on the LHS
that vectors are different from scalars, and on the RHS to treat
vectors as indistinguishable from scalars.
This is especially disappointing because better alternatives exist,
better in the sense that at little or no cost, they establish concepts
that can be generalized to higher dimensions. One zero-cost
alternative would be to say that one vector is “directed to the
right” while the other is “directed to the left”. This makes use
of the idea that a vector has magnitude and direction, which is true
in any number of dimensions, from one on up. As another alternative,
at small cost one could introduce a basis vector γ and say that
the first vector is directed in the +γ direction while the
other is directed in the −γ direction.
- 42.
(–) On page III-84ff: In the chapter on energy, there is a
1.5-page-long section giving examples illustrating the idea of
spontaneity and irreversibility. To all appearances, these are meant
to illustrate some property of energy. There is one sentence, buried
in the middle of a paragraph on page I-86, where the second law of
thermodynamics is mentioned, and a Philadelphia lawyer might argue
that because of this one sentence, the whole section is technically
correct. However, no matter what the technicalities, this section is
the epitome of bad pedagogy. It is entirely inappropriate to feature
these examples in a chapter on energy. After reading this section,
students will be more confused than before ... confused about two of
the most centrally important ideas in physics: entropy and energy.
- 43.
(–) On page III-67: It says «We shall reserve the word “heat”
for a new idea: The interaction we perceive to be associated with
temperature changes.» This clearly violates the principle of “idea
before name” to which the book pays so much lip service.
The name is introduced concurrently with a “definition”.
What’s worse, this is a terrible “definition”, and it is
immediately contradicted by the examples on page III-68, and by the
redefinition on page III-69. Not until page III-124 do we see the
usual textbook definition of “heat” (which itself is not a very good
definition, either, by the way).
The book introduces the terms “sensible heat” and “latent heat”
without ever giving reliable definitions for them.
- 44.
(–) On page III-69: It says «We say that heat is gained by, or
transferred to, systems when their temperature increases (or when they
melt) in thermal interactions, and we say that heat is lost by, or
transferred out of, systems that decrease in temperature (or
freeze).» This is yet another definition of “heat”, which
contradicts the previous definition (item 43) and also
contradicts later definitions (item 52 and
item 55).
This misdefinition mentions melting, but fails to mention evaporation,
sublimation, demagnetization, et cetera.
- 45.
(–) On page III-67ff: The chapter on “Heat” spends many
pages offering the student the idea of heat as a conserved quantity.
A Philadelphia lawyer would argue that the author didn’t say anything
wrong, since he put the wrong ideas into the mouths of Joseph Black
and other historical figures ... but the unsuspecting student will
not appreciate that distinction.
On page III-71 the book coyly asks the student to explain «Why does
Eq. 3.2.4 suggest that the quantity we have invented may be
conserved?» Basic pedagogical principles tell us that ideas that
students come to on their own are more deeply seated than ideas that
are merely told to them. Alas, here the student is asked to form,
based on a sizable collection of evidence, his own notion of
conservation of heat. It is not until page III-116 that there is a
clear indication that heat can be created from scratch. It is not
until page III-122 that there is a clear indication that heat can be
converted to motion.
Black believed that “sensible heat” and “latent heat” were state
functions. The book does nothing to prevent students from believing
the same thing.
This seems like the epitome of bad pedagogy. It practically
guarantees that students will come away with deep-seated
misconceptions about heat.
This is an object lesson in the perils of the twistorical approach
as discussed in section 4.
- 46.
(–) On page III-73: Heat capacity is extensive. Specific heat
is intensive. It is ironic that the book preaches the importance of
scaling laws, but fails to apply the most basic scaling checks and
dimensional-analysis checks to statements like this.
- 47.
(–) On page III-81:
It says:
«You can strengthen your insight into these concepts by now returning
to the discussion of impulse and change of momentum in Section 1.9.
Notice that impulse, like quantity of heat transferred, is path
dependent. In order to calculate an impulse, we must know how the
force delivering the impulse varied instant by instant (i.e., we must
know the "path" of the force with respect to the succession of clock
readings). If we have this information, we can evaluate the impulse
as an integral (i.e., an area under a graph). The situation with
respect to transfer of heat is exactly analogous: Delivery of
impulse (which is not a state variable) results in a change in the
state variable called "momentum." Transfer of heat (which is not a
state variable) at constant pressure results in a change of the state
variable temperature.»
The quoted passage has more errors than it has sentences.
One of the central points that this section tries to make is actually
valid, if you take it out of context, and re-interpret it in just the
right way: It is true that in non-cramped thermodynamics, there is no
path-independent value for ∫ TdS.
Alas, Teaching Introductory Physics buries this fact under three layers of wrong physics, plus a
few layers of bad pedagogy.
-
The definition of “path dependent” is deeply flawed;
see item 48.
- The characterization of “heat” given here is flawed; see
item 52.
- The analogy between impulse and heat is flawed;
see item 49.
- Even if the analogy were overhauled so as to make it correct, it
would violate the pedagogical principle that learning proceeds from
the known to the unknown. If students don’t know about
thermodynamics, you can’t explain it to them in terms of
non-conservative force fields (which they don’t know about, either).
- This makes a mockery of the of principle of “idea before
name” to which the book gives so much lip service. The title of
this section is «HEAT IS NOT A FUNCTION OF STATE». If
you learn those words by rote, they may turn out to be correct,
if you later learn a correct definition for the words. However,
the ideas that Teaching Introductory Physics attaches to these words are not correct.
- It is questionable (both from a pedagogical and from a
practical point of view) to emphasize what something is
not. Even if the book gave a consistent definition of
“heat” and a correct definition of “path independent” (which
it does not), saying that heat is not path independent should not
be the goal; it is barely even a starting place. It would have
been more constructive to explain that T dS is a state
function, and to explain some of the things we can do with it.
The book does not correctly explain the relationship between
TdS (which is a function of state) and ∫ TdS (which is
not). This could have been explained using pictures, such as the
picture of uncramped thermodynamics in reference 7. See
also reference 13.
- 48.
(–) On page III-81: The definition of “path
dependent” given here is wrong. As discussed in
item 39, the key question is not asked, let alone
answered.
- 49.
(–) On page III-81: The statement (quoted in
item 47) about impulse might have been correct
if it had considered paths through position-space instead of
state-space. In particular, paths through the position-space inside
a betatron can produce a path-dependent impulse, since momentum is
not a function of position there, as discussed in
reference 14.
However, the quoted statement is clearly talking about paths in
state-space. That changes everything, because momentum is a
function of state ... not a function of position per se, but a
function of state. That allows us to carry out the following
calculation:
|
impulse | | = | | | | along some path from state A to state B |
| | | = | | |
| | | = | | |
| | | = | | p(B) − p(A) | | independent of path in state-space
|
| (7)
|
- 50.
(–) On page III-81: Introducing the term «delivery of impulse»
violates the principle of “idea before name”. If this term means
anything, it presumably is the same as transfer of momentum.
- 51.
(–) On page III-81: Saying that impulse is path-dependent is
tantamount to saying that the force field is non-grady. As a
pedagogical point, just telling students that such a field
exists is next to pointless. Students have a strong tendency to
assume that every force field is the gradient of some potential. If
you want ’em to believe in (let alone understand) non-grady force
fields, it will take some serious work, not just a sentence or two
here and there. Teaching Introductory Physics doesn’t offer any diagrams of a non-grady
field, and doesn’t mention any concrete real world examples (such as
a betatron). The analogy to “some” force field is neither
concrete nor correct; see item 49. Diagrams would
have been a big help, as in reference 13.
- 52.
(–) On page III-81: It says «Transfer of heat (which is
not a state variable) at constant pressure results in a change of the
state variable temperature.» I assume this is meant to be a general
rule, since is not restricted to any particular scenario, and no
limits to the validity of this statement are given. This rule
more-or-less agrees with the “definition” given in
item 43, but disagrees with the “definitions” given in
item 43, item 44, and item 55.
This rule is inconsistent with basic physics in this context; it is
simply not true that heat transfers of the kind considered in this
paragraph always result in a change of temperature.
- 53.
(–) On page III-122: The book explains that “living
force” is an old term for kinetic energy, then quotes James Joule
(1847) as being “inclined to believe that both of these hypotheses
will be found to hold good — that ... sensible heat will be found to
consist in the living force of the particles of the bodies in which it
is induced....” Joule was appropriately cautious. The book is not
cautious; it boldly says «[Joule’s hypothesis turned out to be
correct.]»
Alas, Joule’s hypothesis is not correct. The KE/PE distinction does
not parallel the heat/latent-heat distinction. Not all kinetic energy
is thermal, and not all thermal energy is kinetic. See
reference 7.
- 54.
(–) On page III-123: Although the book repeatedly emphasizes the
principle of “idea before name”, it introduces the term “thermal
energy” without ever explaining what that means. Is it the same as
caloric? Is it a function of state? How is it related to “sensible
heat” and/or “latent heat”?
- 55.
(–) On page III-124: It says «We reserve the term “transfer of
heat” to situations in which thermal energy is transferred from a
system at higher temperature to a system at lower temperature without
any displacements that involve the doing of work by one system on
the other.» This is yet another “definition” of heat. This
contradicts the “definitions” given in item 43,
item 44, and item 52. This pays
lip-service to a particular approach that is popular in the PER
literature, but is not actually a good idea.
- 56.
(–) On page III-126: The book states the first law in the form
which is not a good idea in general. It wouldn’t be so bad if this
formula were advertised as an approximate or introductory idea, but on
the contrary, the book utterly fails to recognize the weaknesses of
this approach. It says equation 8 «always holds».
Counterexamples are easy to find, including a wide range of
dissipative phenomena, as in item 57 and in the
grindstones discussed in reference 7. Another wide class
of counterexamples involves advection, also discussed in
reference 7.
Compare item 22.
- 57.
(–) On page III-137ff: The whole section 4.22 (“Work and
Heat in the Presence of Sliding Friction”) is worse than useless. It
consists of bad details in the service of a bad goal.
In previous sections the book defined (after a fashion) W and Q
and E, and said that the equation 8 «always holds». Many
properties of W were explored, including the work/KE theorem.
Now in section 4.22 an impartial observer would see strong evidence
that equation 8 does not hold. Rather than analyzing things
impartially, the book brutally redefines W so as to make
equation 8 hold. The redefinition is based on the assumption
that equation 8 should hold, so the result is a meaningless
circular argument.
There is no recognition that the redefinition breaks much of the
previous development, including the work/KE theorem.
In any situation where dissipation is involved, this approach
invalidates the foundations of classical thermodynamics, and leaves us
with nothing. In particular it invalidates the idea that there is a
meaningful separation between the macroscopic phenomena (W) and
thermal phenomena (Q) as in equation 8. Once you start
including “some” unobservable microscopic phenomena in W, it is no
longer clear what (if anything) is meant by Q.
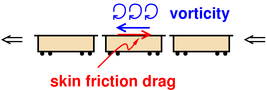
As an example of what I mean, consider the skin friction drag on the
middle car of a long train, as shown in figure 2.
We ignore pressure drag and pressure recovery acting on the front and
rear of this car (since they nearly cancel by symmetry), which means
skin friction drag is the dominant contribution to the drag. It
imparts rightward momentum to the leftward-moving train (as shown by
the red arrow) and the same process imparts leftward momentum to the
ambient air (as shown by the blue arrow). It would be nice to have a
work/KE theorem that included this drag force, but Teaching Introductory Physics leaves us
without one.
The book’s approach is a travesty of science and logic. It is akin to
the ad-hoc arguments attributed to Faust in section 4.23.
This also makes a mockery of the so-called historical approach, since
the relationship between work and frictional heating has been known
since 1798, and should have been taken into account when Q and
W were first introduced. Actually the book recognized this problem
in the opening sentences on page III-iii (item 38).
But the problem, having been recognized, is never solved.
There are ways in which this problem could have been solved, but
they are not hinted at in the book. In a small sense the work/KE
theorems can be rescued as discussed in reference 12. In a
much larger sense thermodynamics can be rescued by giving up on
work (W) and heat (Q) and instead talking about energy and
entropy, as in reference 7.
As far as I can tell, the word “entropy” does not appear in the
book. It is definitely not in the index or the table of contents.
Does it appear in the body of the text? If so, it is very
inconspicuous. That is really quite astonishing.
|
You can’t do thermodynamics without entropy.
|
|
|
|
- 58.
(+) On page III-147: The quote from Percy Bridgman
explains that the law of conservation of energy is falsifiable, i.e.
not merely a convention or assumption.
In many places, this book follows the “historical approach” as a way
to motivate and to organize an introductory-level course. This is not
good.
An introductory course should keep things simple and straightforward.
Real history is neither simple nor straightforward. The real history
of science is a tale of confusion, with much backtracking out of blind
alleys. Nobody would be so foolish as to inflict the real history on
introductory-level students.
There is no law that says pedagogy must recapitulate phylogeny. In
introductory classes we should use the best available evidence, not
the most ancient evidence. For more on this, see reference 16.
I have the greatest respect for real history and real historians. If
someone really wants to study the history of science, that’s
commendable. The history of science is advanced topic, suitable for
those who already have a good grasp of science and a good grasp of
historical methods. Please do not confuse introductory physics with
the history of physics.